Mathematik GWM5 GWM6 GWM7 GWM8 GWM9 SchulheftM5 SchulheftM6 SchulheftM10 SchulheftM11
1. Integralrechnung
1.1 Das bestimmte Integral
Einfache Eigenschaften des bestimmten Integrals
1) Vorzeichen
2) Symmetrische Funktionen
3) Abschnittsweise Integration
1.2 Die Integralfunktion
1.3 Der Hauptsatz der Differential- und Integralrechnung (HDI)
Verfahren zur Berechnung bestimmter Integrale mit Hilfe einer Stammfunktion
1.4 Stammfunktionen und unbestimmtes Integral
Besondere Fälle für Stammfunktionen
1.5 Flächenberechnungen mit dem Integral
1) Fläche zwischen dem Graphen und der x-Achse
2) Fläche zwischen den Graphen zweier Funktionen
3) Uneigentliche Integrale - ins Unendliche reichende Flächen
2. Die Krümmung von Graphen und ihre Wendepunkte
2.1 Die zweite Ableitung
2.2 Krümmung
2.3 Wendepunkte
2.4 Art der Extrema
3. Zufallsgrößen, Kombinatorik und Binomialverteilung
3.1 Zufallsgrößen
Eine Funktion  , die jedem Ergebnis
, die jedem Ergebnis  eine reele Zahl
eine reele Zahl  zuordnet, heißt Zufallsgröße oder Zufallsvariable
zuordnet, heißt Zufallsgröße oder Zufallsvariable  auf
auf  .
.
Die Funktion  , die jedem Wert
, die jedem Wert  der Zufallsgröße
der Zufallsgröße  eine Wahrscheinlichkeit
eine Wahrscheinlichkeit  zuordnet, heißt Wahrscheinlichkeitsverteilung oder Wahrscheinlichkeitsfunktion der Zufallsgröße
zuordnet, heißt Wahrscheinlichkeitsverteilung oder Wahrscheinlichkeitsfunktion der Zufallsgröße  .
.

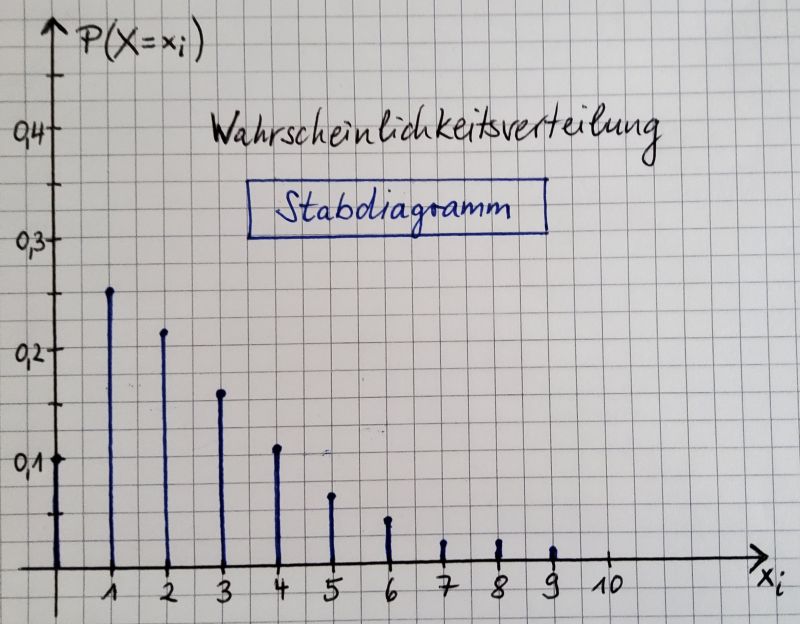
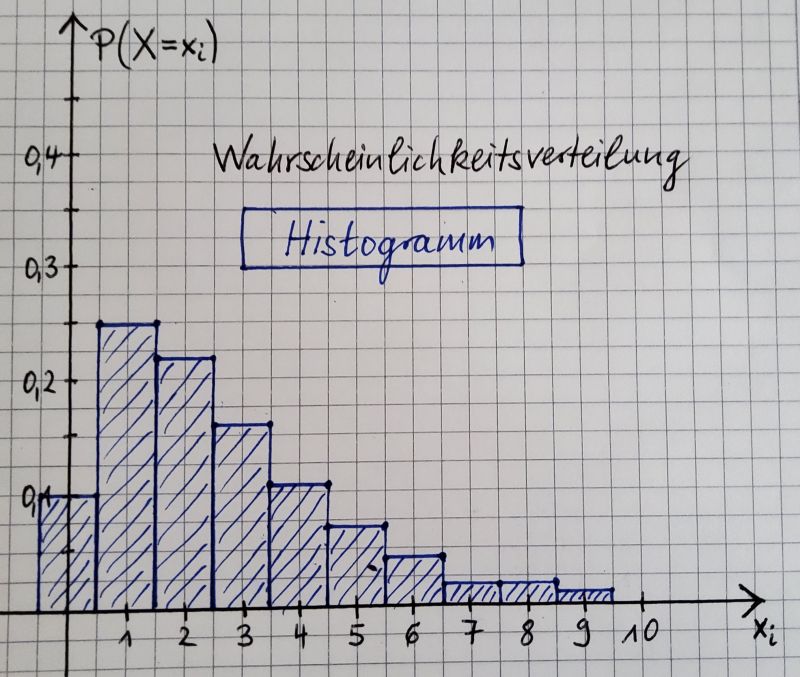
Als Graph verwendet man dabei Stabdiagramme bzw. Histogramme.
Die Funktion  , die jedem Wert
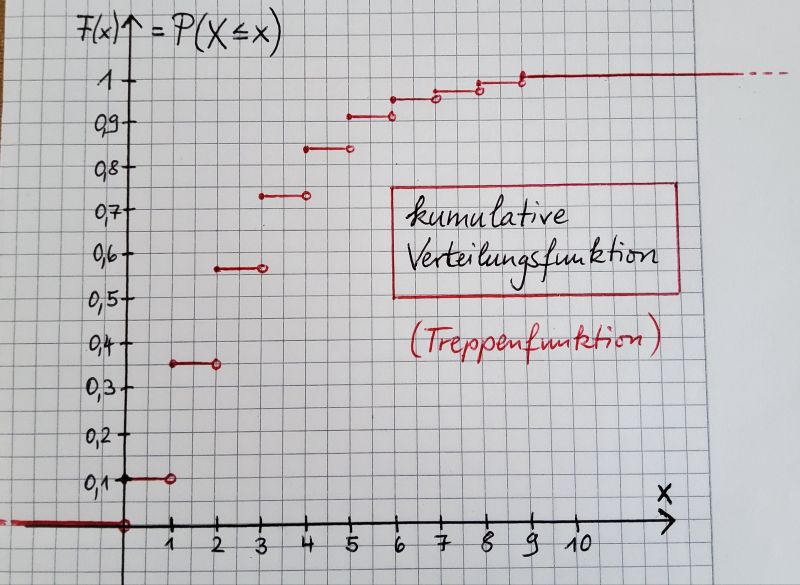
, die jedem Wert  die Wahrscheinlichkeit "bis zu diesem Wert" zuordnet, heißt kumulative Verteilungsfunktion der Zufallsgröße
die Wahrscheinlichkeit "bis zu diesem Wert" zuordnet, heißt kumulative Verteilungsfunktion der Zufallsgröße  .
.
Als Graph ergibt sich dabei eine Treppenfunktion.
3.2 Erwartungswert und Varianz
Wenn  die möglichen Werte einer Zufallsgröße
die möglichen Werte einer Zufallsgröße  sind, so heißt die reelle Zahl
sind, so heißt die reelle Zahl

|
der Erwartungswert der Zufallsgröße  .
.
Kurzschreibweise: 
Eine Messgröße für die Streuung der Werte  einer Zufallsgröße
einer Zufallsgröße  um den Erwartungswert herum ist die sogenannte Varianz bzw. Standardabweichung.
um den Erwartungswert herum ist die sogenannte Varianz bzw. Standardabweichung.
Wenn  die möglichen Werte einer Zufallsgröße
die möglichen Werte einer Zufallsgröße  mit dem Erwartungswert
mit dem Erwartungswert  sind, so heißt die reelle Zahl
sind, so heißt die reelle Zahl

|
die Varianz der Zufallsgröße  .
.
Da dies eine quadratische Größe ist, die nicht so anschaulich ist, hat man zur Beurteilung der Abweichung vom Erwartungswert die sogenannte Standardabweichung eingeführt:
Standardabweichung  der Zufallsgröße der Zufallsgröße 
|
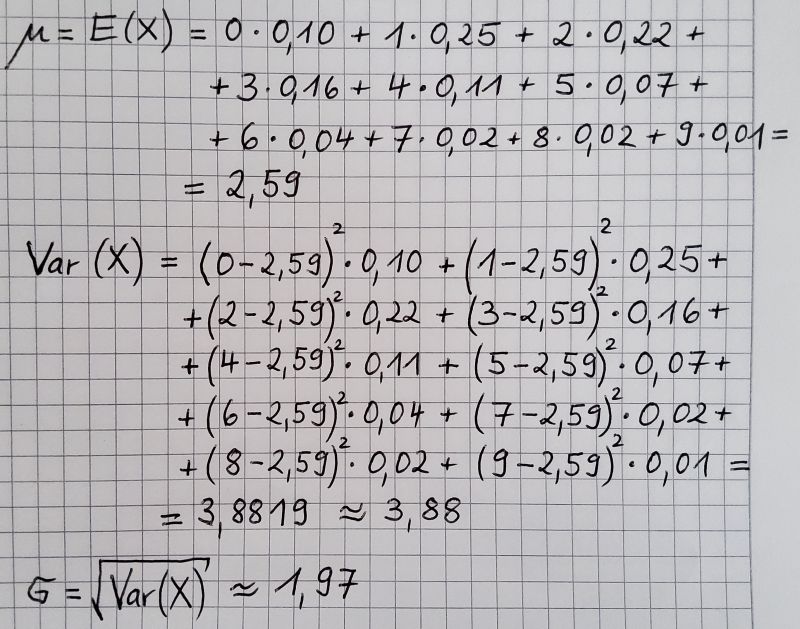
Standardabweichung und Varianz einer Zufallsgröße von Mathehoch13 bei YouTube.com
Varianz- und Standardabweichung Kurs bei unterricht.de
3.3 Kombinatorik
In der Kombinatorik steht stets die Frage nach der Anzahl der Möglichkeiten bei einem Zufallsexperiment im Fokus.
Will man die Wahrscheinlichkeit eines Ereignisses  eines Laplace-Experiments bestimmen, interessiert man sich für die Anzahl der Elemente des Ergebnisraums
eines Laplace-Experiments bestimmen, interessiert man sich für die Anzahl der Elemente des Ergebnisraums  und die Anzahl der Elemente des Ereignisses
und die Anzahl der Elemente des Ereignisses  .
.
Hierfür liefert die Kombinatorik wichtige Abzählmethoden die auf dem allgemeinen Zählprinzip beruhen.
Wird ein Zufallsexperiment in  Stufen durchgeführt und gibt es in der ersten Stufe Stufen durchgeführt und gibt es in der ersten Stufe  , in der zweiten Stufe , in der zweiten Stufe  und in der und in der  -ten Stufe -ten Stufe  mögliche Ergebnisse, so gilt für die Anzahl mögliche Ergebnisse, so gilt für die Anzahl  der insgesamt möglichen Ergebnisse: der insgesamt möglichen Ergebnisse: 
|
- Beispiel: Wie viele vierstellige Zahlen gibt es, die eine 7 an der Hunderterstelle haben?
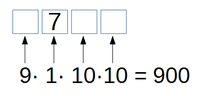
- Beispiel: Wie viele fünfstellige Zahlen gibt es, die nur aus Ziffern kleiner als 7 bestehen?
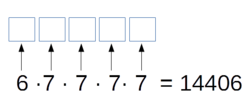
Zählprinzip Erklärvideo von mathegym.de bei YouTube.com
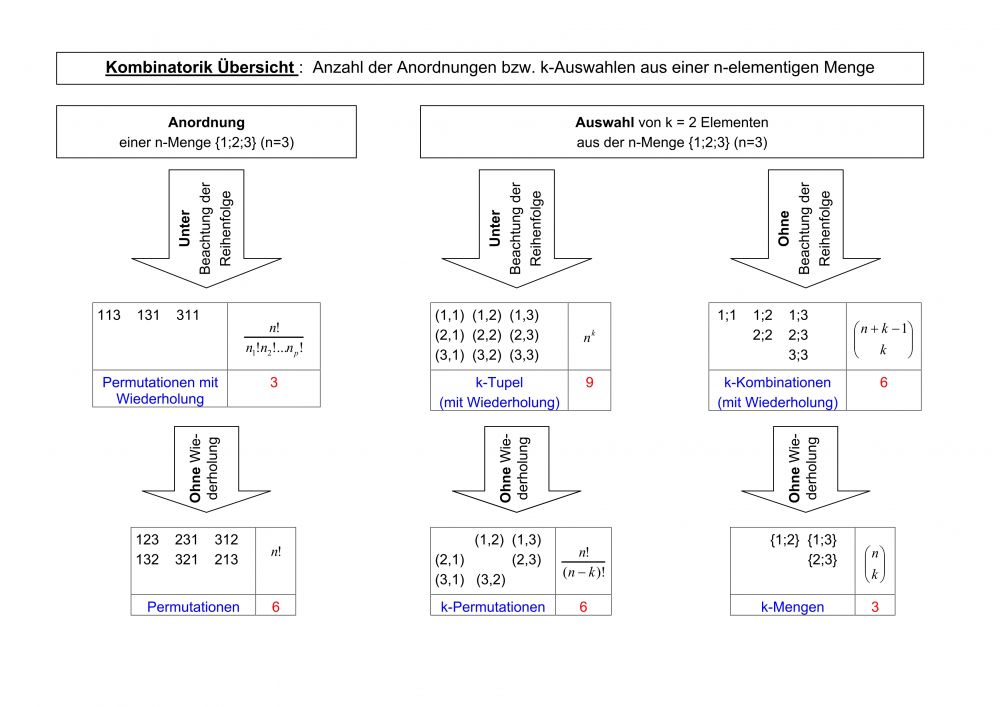 Kombinatorik - eine Übersicht zu kombinatorischen Grundproblemen
Kombinatorik - eine Übersicht zu kombinatorischen Grundproblemen

|

|
Ein Urnenmodell ist ein Gedankenexperiment, das in der Stochastik verwendet wird, um verschiedene Zufallsexperimente auf einheitliche und anschauliche Weise zu modellieren. Dazu wird ein fiktives Gefäß, Urne genannt, mit einer bestimmten Anzahl an Kugeln gefüllt, die anschließend zufällig gezogen werden. Damit ist gemeint, dass bei jedem Zug alle in der Urne befindlichen Kugeln die gleiche Wahrscheinlichkeit haben, ausgewählt zu werden. Dadurch kann die Bestimmung der Wahrscheinlichkeiten auf die Lösung kombinatorischer Abzählprobleme zurückgeführt werden.
Man unterscheidet Ziehungen mit Zurücklegen, bei denen jede Kugel nach ihrer Registrierung wieder in die Urne zurückgelegt wird, von Ziehungen ohne Zurücklegen, bei denen eine einmal gezogene Kugel nicht wieder zurückgelegt wird. Viele wichtige Wahrscheinlichkeitsverteilungen, wie beispielsweise die Binomialverteilung oder die hypergeometrische Verteilung können mit Hilfe von Urnenmodellen hergeleitet und veranschaulicht werden.
Gemischte Aufgaben der Kombinatorik Kurs bei unterricht.de
3.4 Bernoulli-Experimente
Zufallsexperimente, bei denen man sich nur für zwei Ergebnisse (Treffer/Niete) interessiert, werden als Bernoulli-Experimente bezeichnet.
Symbole: 0: Niete; 1: Treffer; Trefferwahrscheinlichkeit  ; Nietenwahrscheinlichkeit
; Nietenwahrscheinlichkeit  ;
;
- Beispiele: (1) Werfen einer Münze:
 ; (2) Sechs und Nicht-Sechs beim Würfeln:
; (2) Sechs und Nicht-Sechs beim Würfeln:  ; (3) Ja/Nein- und Ein/Aus-Experimente;
; (3) Ja/Nein- und Ein/Aus-Experimente;
Eine Bernoulli-Kette ist eine Folge von  unabhängigen Bernoulli-Versuchen mit der Trefferwahrscheinlichkeit
unabhängigen Bernoulli-Versuchen mit der Trefferwahrscheinlichkeit  .
.
 heißt auch Länge der Bernoulli-Kette.
heißt auch Länge der Bernoulli-Kette.
Gesucht: Wahrscheinlichkeit, dass bei einer Bernoulli-Kette der Länge  genau
genau  Treffer erhalten werden, wobei die Trefferwahrscheinlichkeit
Treffer erhalten werden, wobei die Trefferwahrscheinlichkeit  ist.
ist.
Diese wird oft mit  oder
oder  bezeichnet. (
bezeichnet. ( : Anzahl der Treffer)
: Anzahl der Treffer)
Baumdiagramme zu Bernoulli-Ketten bis zur Länge von n=4 beim Landesbildungsserver Baden-Württemberg
Formel von Bernoulli von J. van Lück bei geogebra.org
Bernoullische Formel:
 mit mit 
|
Die zugehörige Wahrscheinlichkeitsverteilung  heißt Binomialverteilung mit den Parametern n und p.
heißt Binomialverteilung mit den Parametern n und p.
- Erwartungswert und Varianz der Binomialverteilung
4. Beurteilende Statistik
4.1 Alternativ-Tests
4.2 Signifikanztests
5. Geraden und Ebenen im Raum
5.1 Lineare Abhängigkeit von Vektoren
- Sind mehrere Vektoren
 gegeben, so lassen sich damit beliebig viele Vektoren
gegeben, so lassen sich damit beliebig viele Vektoren  der Form
der Form

|
erzeugen. Dann heißt  eine Linearkombination der Vektoren
eine Linearkombination der Vektoren  .
.

 ist also eine Linearkombination aus den Vektoren
ist also eine Linearkombination aus den Vektoren  und
und  .
.
Die Vektoren  heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination der anderen Vektoren darstellbar ist. Sonst heißen diese Vektoren linear unabhängig. heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination der anderen Vektoren darstellbar ist. Sonst heißen diese Vektoren linear unabhängig.
|
Prüfen Sie die Vektoren  auf lineare Abhängigkeit!
auf lineare Abhängigkeit!
Lösung: Mit Hilfe des zugehörigen Gleichungssystem (mit drei Gleichungen und zwei Unbekannten) findet man heraus, dass diese drei Vektoren linear unabhängig sind, da es keine Zahlen  und
und  gibt, so dass
gibt, so dass  .
.
Im zweidimensionalen Vektorraum  gibt es maximal zwei linear unabhängige Vektoren. gibt es maximal zwei linear unabhängige Vektoren.
Im dreidimensionalen Vektorraum  gibt es maximal drei linear unabhängige Vektoren. gibt es maximal drei linear unabhängige Vektoren.
Jeder weitere Vektor lässt sich also eindeutig als Linearkombination dieser linear unabhängigen Vektoren darstellen.
|
- Bemerkung zum besseren Verständnis:
Im  gilt:
gilt:
| Zwei Vektoren sind linear abhängig genau dann, wenn diese beiden Vektoren parallel (bzw. antiparallel) sind.
Drei Vektoren sind linear abhängig genau dann, wenn diese drei Vektoren parallel zu einer Ebene sind.
|
Siehe Linear abhängig in 2 Dimensionen und Linear abhängig in 3D von Dr. Marie-Luise Herrmann mit GeoGebra
5.2 Geraden
Geradengleichungen
Siehe Parameterform der Geradengleichung von Frank Dill bei GeoGebra
Der Ortsvektor eines beliebigen Punktes  auf einer Geraden
auf einer Geraden  mit dem Aufpunkt
mit dem Aufpunkt  (und dem zugehörigen Ortsvektor
(und dem zugehörigen Ortsvektor  ) und dem Richtungsvektor
) und dem Richtungsvektor  lässt sich schreiben als:
lässt sich schreiben als:

|
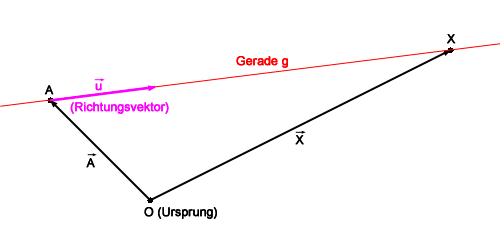

ist die Geradengleichung der Gerade  durch den Punkt
durch den Punkt  mit dem Richtungsvektor
mit dem Richtungsvektor  .
.
Wann liegt ein Punkt auf einer Geraden?
Ein Punkt liegt genau dann auf einer Geraden, wenn beim Einsetzen der Koordinaten des Punktes in die Geradengleichung (für  ) mit einem festen Parameterwert
) mit einem festen Parameterwert  eine wahre Aussage entsteht.
eine wahre Aussage entsteht.
Dazu muss der passende Parameterwert für  natürlich noch gefunden werden. Gelingt dies nicht, so liegt der Punkt nicht auf der Geraden.
natürlich noch gefunden werden. Gelingt dies nicht, so liegt der Punkt nicht auf der Geraden.
Besondere Geraden
 -Achse:
-Achse:  ,
,  -Achse:
-Achse:  und
und  -Achse:
-Achse: 
Sind zwei Koordinaten im Richtungsvektor null, dann ist die Gerade parallel zu einer Koordinatenachse.
Zum Beispiel ist  parallel zur
parallel zur  -Achse.
-Achse.
Ist eine Koordinate im Richtungsvektor null, dann ist die Gerade parallel zu einer Koordinatenebene.
Zum Beispiel ist  parallel zur
parallel zur  -Ebene oder
-Ebene oder  parallel zur
parallel zur  -Ebene.
-Ebene.
Spurpunkte
Die Spurpunkte einer Geraden sind deren Schnittpunkte mit den Koordinatenebenen.
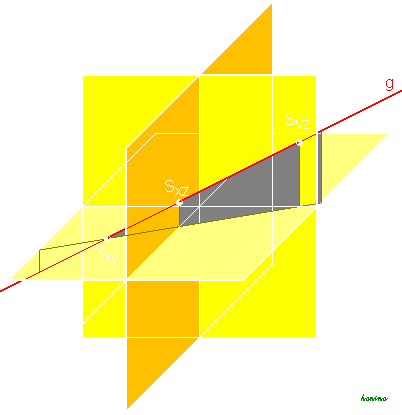

Spurpunkt  mit der
mit der  -Ebene: In dieser Ebene gilt:
-Ebene: In dieser Ebene gilt: 
 , also
, also  .
.
Spurpunkt  mit der
mit der  -Ebene: Dort gilt:
-Ebene: Dort gilt: 
 , also
, also  .
.
Spurpunkt  mit der
mit der  -Ebene: Dort gilt:
-Ebene: Dort gilt: 
 , also
, also  .
.
Gegenseitige Lage von Geraden
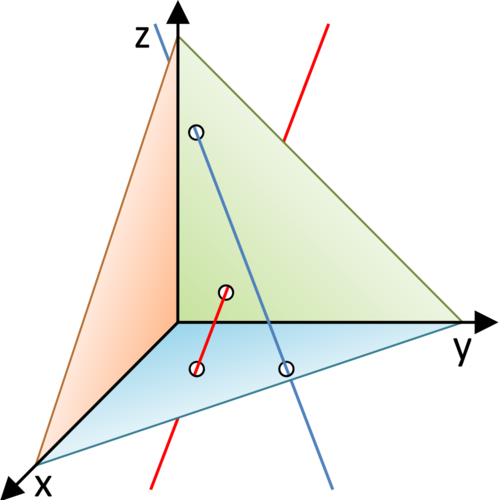
Seien zwei Geraden  und
und  gegeben.
gegeben.
Dann gibt es vier mögliche gegenseitige Lagen im Raum (siehe Abbildung im Buch S. 125):
a) Identische Geraden
Die beiden Richtungsvektoren  und
und sind linear abhängig, d.h
sind linear abhängig, d.h  und der Aufpunkt
und der Aufpunkt  der Geraden
der Geraden  liegt auf
liegt auf  .
.
b) Parallele Geraden
Die beiden Richtungsvektoren  und
und sind linear abhängig, d.h
sind linear abhängig, d.h  und der Aufpunkt
und der Aufpunkt  der Geraden
der Geraden  liegt nicht auf
liegt nicht auf  .
.
c) Sich schneidende Geraden
Die beiden Richtungsvektoren  und
und sind linear unabhängig, d.h
sind linear unabhängig, d.h  und das Gleichsetzen der beiden Geradengleichungen liefert eine Lösung. Den Schnittpunkt bestimmt man, indem man die Geradengleichungen gleichsetzt bzw. ineinander einsetzt.
und das Gleichsetzen der beiden Geradengleichungen liefert eine Lösung. Den Schnittpunkt bestimmt man, indem man die Geradengleichungen gleichsetzt bzw. ineinander einsetzt.
d) Windschiefe Geraden
Die beiden Richtungsvektoren  und
und sind linear unabhängig, d.h
sind linear unabhängig, d.h  und das Gleichsetzen der beiden Geradengleichungen liefert keine Lösung.
und das Gleichsetzen der beiden Geradengleichungen liefert keine Lösung.
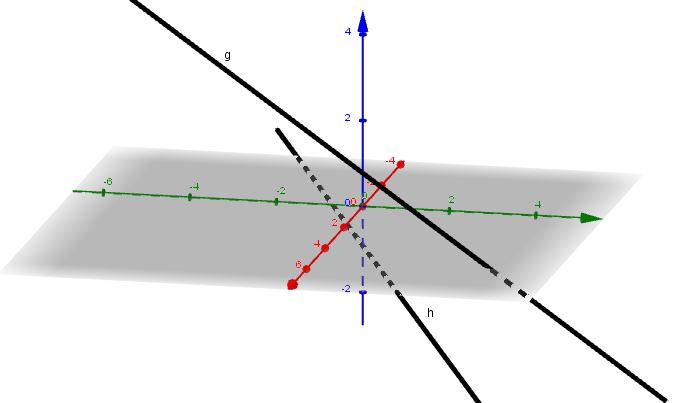
Untersuchen Sie die gegenseitige Lage der beiden Geraden  und
und  !
!
Gleichsetzen: 

Dies setzen wir in die anderen beiden Gleichungen ein:


Das ist offensichtlich ein Widerspruch! Also sind die beiden Geraden windschief zueinander (da sie ja auch nicht parallel zueinander sind).
5.3 Ebenen
Ebenengleichungen
Siehe Parameterform bei Ebenen verstehen von Birgit Lachner bei GeoGebra
Der Ortsvektor eines beliebigen Punktes  auf einer Ebene
auf einer Ebene  mit dem Aufpunkt
mit dem Aufpunkt  (und dem zugehörigen Ortsvektor
(und dem zugehörigen Ortsvektor  ) und den beiden Richtungsvektoren
) und den beiden Richtungsvektoren  lässt sich schreiben als:
lässt sich schreiben als:

|
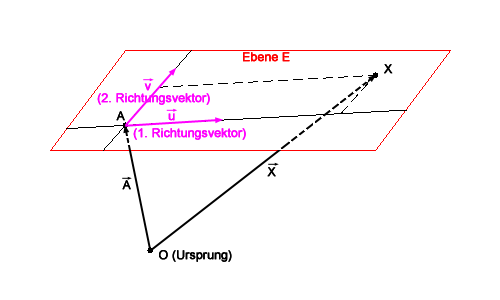

ist die Ebenengleichung der Ebene  durch den Punkt
durch den Punkt  mit den Richtungsvektoren
mit den Richtungsvektoren  und
und  .
.
Wann liegt ein Punkt auf einer Ebene?
Ein Punkt liegt genau dann auf einer Ebene, wenn beim Einsetzen der Koordinaten des Punktes in die Ebenengleichung (für  ) mit festen Parameterwerten
) mit festen Parameterwerten  eine wahre Aussage entsteht.
eine wahre Aussage entsteht.
Dazu müssen passende Parameterwerte für  und
und  natürlich noch gefunden werden. Gelingt dies nicht, so liegt der Punkt nicht auf der Ebene.
natürlich noch gefunden werden. Gelingt dies nicht, so liegt der Punkt nicht auf der Ebene.
Spurgeraden
Die Schnittgeraden einer Ebene mit den Koordinatenebenen heißen Spurgeraden. Durch sie bekommt man einen Überblick über die Lage einer Ebene im Koordinatensystem.
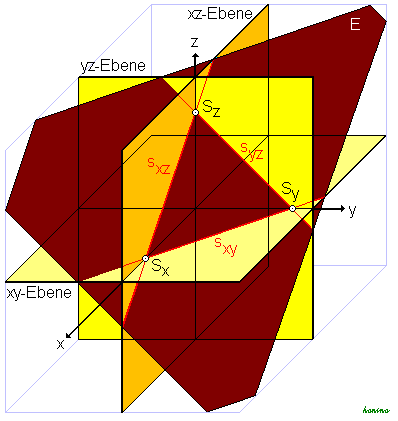
Siehe Spurgeraden einer Ebene von Thorsten Glaser bei GeoGebra
Normalenformen der Ebenengleichung
Betrachte die Ebene  .
.
Sei  ein Normalenvektor auf die beiden Richtungsvektoren
ein Normalenvektor auf die beiden Richtungsvektoren  und
und  , also auch ein Normalenvektor auf die Ebene
, also auch ein Normalenvektor auf die Ebene  .
.
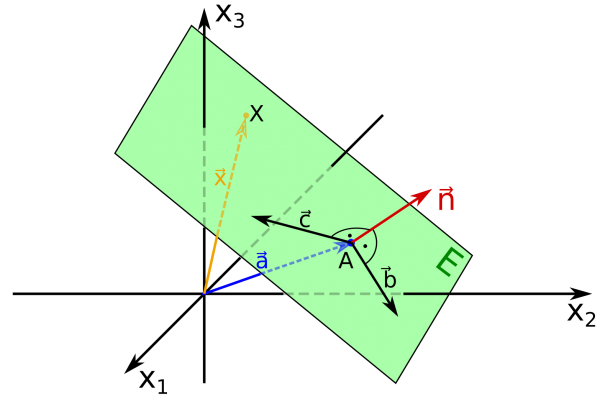
Dann gilt:  und
und  , weil die Vektoren ja jeweils senkrecht aufeinander stehen.
, weil die Vektoren ja jeweils senkrecht aufeinander stehen.
Multipliziert man nun (mit Skalarprodukt!) die Ebenengleichung auf beiden Seiten mit dem Normalenvektor  durch, so entsteht:
durch, so entsteht:

 und somit ergibt sich
und somit ergibt sich
die vektorielle Normalenform der Ebenengleichung

|
Schreibt man diese mit den Koordinaten der Vektoren aus, so entsteht
die skalare Normalenform der Ebenengleichung

|
mit 
Diese Form wird auch Koordinatendarstellung oder Koordinatengleichung der Ebene genannt.

soll von der Parameterform in die Normalenform umgewandelt werden.
 ist ein Vektor, der auf beiden Richtungsvektoren senkrecht steht.
ist ein Vektor, der auf beiden Richtungsvektoren senkrecht steht.
Wir wählen günstigerweise als Normalenvektor  .
.
Dann ist  .
.
Die skalare Normalenform der Ebenengleichung ist also:  .
.
In Vektordarstellung ist die Normalenform der Ebenengleichung: ![{\displaystyle {\begin{pmatrix}1\\0\\2\end{pmatrix}}\circ \left[{\vec {x}}-{\begin{pmatrix}0\\-2\\2\end{pmatrix}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e784f1191510f53840e1ecf1746c2cca418bd09)
Hesse'sche Normalenform (HNF)
Benutzt man zum Aufstellen der Normalenform statt  sogar dessen Einheitsvektor
sogar dessen Einheitsvektor  und diesen noch so orientiert, dass
und diesen noch so orientiert, dass  ist, so erhält man die HNF der Ebenengleichung:
ist, so erhält man die HNF der Ebenengleichung:

|
bzw.

|
Diese wird vor allem für Abstandberechnungen von Punkt zu Ebene genutzt. Für den Fall, dass  , nimmt man einfach den Gegenvektor von
, nimmt man einfach den Gegenvektor von  als Normalenvektor und stellt damit die HNF auf.
als Normalenvektor und stellt damit die HNF auf.

soll von der Parameterform in die Hesse'sche Normalenform umgewandelt werden.
Wir brauchen also noch den Einheitsvektor des Normalenvektors  . Dieser ist
. Dieser ist  .
.
Dann ist  .
.
Die skalare HNF der Ebenengleichung ist also:  .
.
In Vektordarstellung ist die HNF der Ebenengleichung: ![{\displaystyle {\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\0\\2\end{pmatrix}}\circ \left[{\vec {x}}-{\begin{pmatrix}0\\-2\\2\end{pmatrix}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b95d16fcbe0e74009e30f133213f952e70f0ddae)
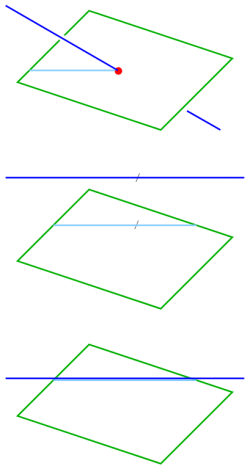
5.4 Gegenseitige Lage von Gerade und Ebene
Schnittpunkt:
Die Richtungsvektoren  und
und  der Ebene und der Richtungsvektor
der Ebene und der Richtungsvektor  der Geraden sind linear unabhängig genau dann, wenn die Ebene und die Gerade sich in einem Punkt schneiden. Den Schnittpunkt bestimmt man, indem man die Geradengleichung und die Ebenengleichung gleichsetzt bzw. ineinander einsetzt.
der Geraden sind linear unabhängig genau dann, wenn die Ebene und die Gerade sich in einem Punkt schneiden. Den Schnittpunkt bestimmt man, indem man die Geradengleichung und die Ebenengleichung gleichsetzt bzw. ineinander einsetzt.
Parallelität:
Die Richtungsvektoren  und
und  der Ebene und der Richtungsvektor
der Ebene und der Richtungsvektor  der Geraden sind linear abhängig genau dann, wenn die Ebene und die Gerade parallel sind. Liegt die Gerade dabei nicht in der Ebene, so spricht man von echt parallel.
der Geraden sind linear abhängig genau dann, wenn die Ebene und die Gerade parallel sind. Liegt die Gerade dabei nicht in der Ebene, so spricht man von echt parallel.
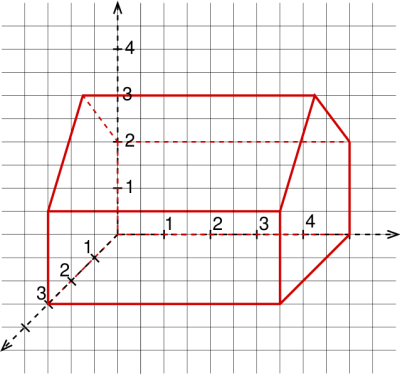
(1) Betrachte das Haus in dem Bild oben. Die Giebelhöhe sei 1,5. Wo schneidet die rechte vordere Dachkante die Bodenebene ( )?
)?
Rechte vordere Dachkante 
Die Bodenebene hat die Gleichung  .
.
Setze  und
und  aus der Geradengleichung in die Ebenengleichung ein:
aus der Geradengleichung in die Ebenengleichung ein: 
 , also
, also  .
.
Einsetzen in die Geradengleichung liefert den Ortsvektor des Schnittpunktes  .
.

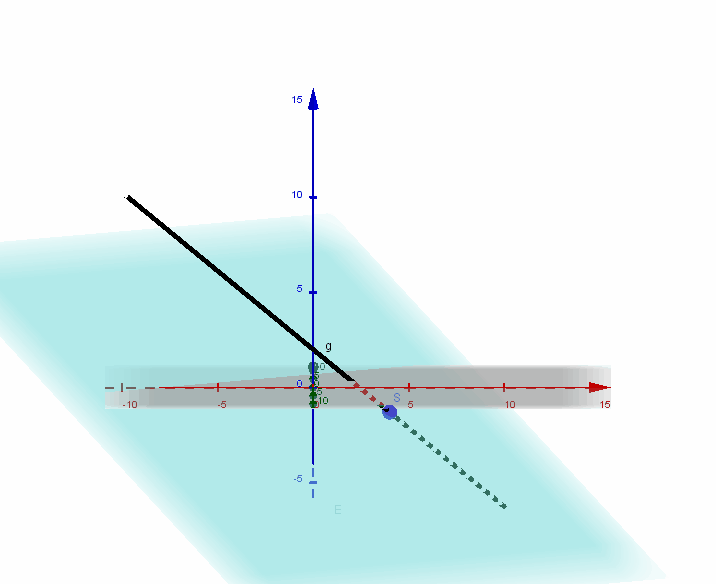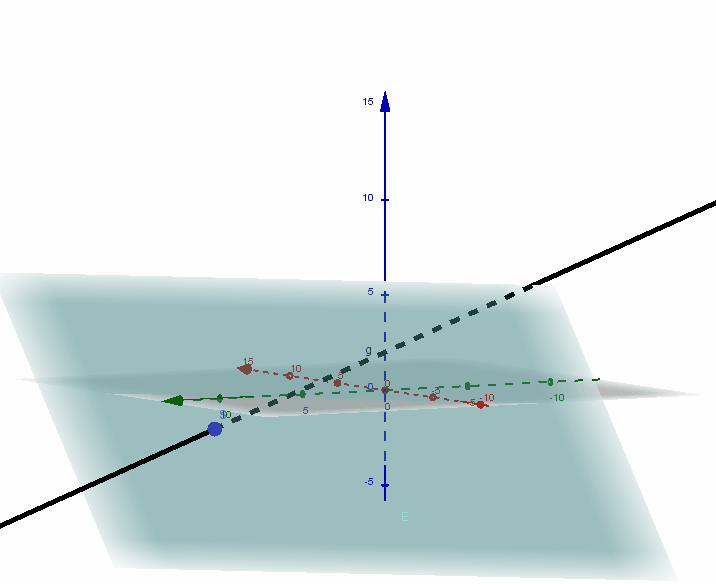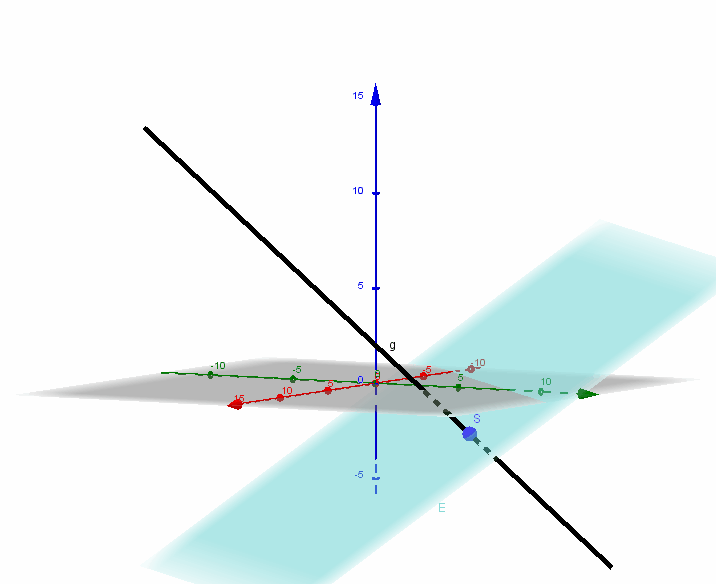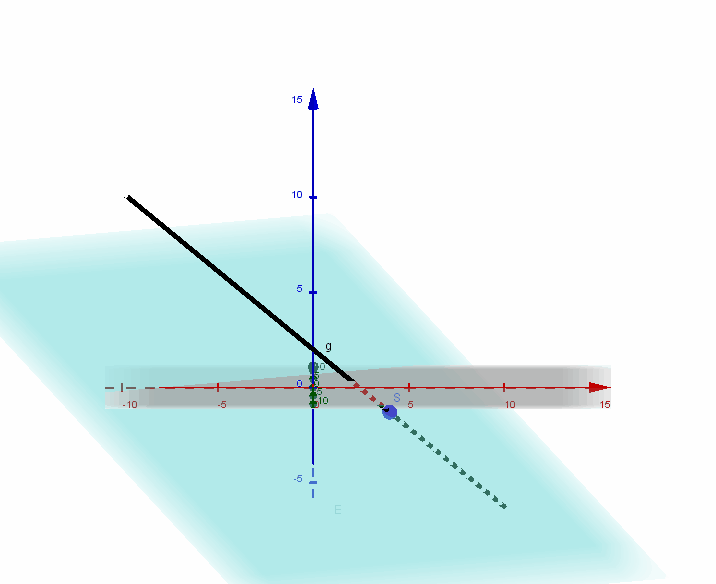
(2) Schnittpunkt von Gerade  und Ebene
und Ebene  ?
?
Setze  und
und  aus der Geradengleichung in die Ebenengleichung ein:
aus der Geradengleichung in die Ebenengleichung ein: 
 , also
, also  .
.
Einsetzen in die Geradengleichung liefert den Ortsvektor des Schnittpunktes  .
.

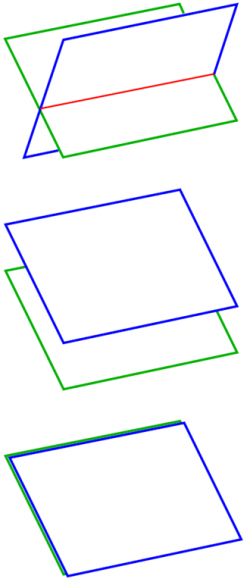
5.5 Gegenseitige Lage von Ebenen
Schnittgerade:
Die Normalenvektoren zweier Ebenen sind linear unabhängig genau dann, wenn die beiden Ebenen eine Schnittgerade gemeinsam haben.
Parallele Ebenen:
Die Normalenvektoren zweier Ebenen sind linear abhängig genau dann, wenn die beiden Ebenen parallel zueinander sind.
(1) Beschreibe die Lage von Ebene  und Ebene
und Ebene  zueinander und stelle gegebenenfalls eine Gleichung der Schnittgerade auf!
zueinander und stelle gegebenenfalls eine Gleichung der Schnittgerade auf!
Wandle die Ebenengleichung von  in Normalenform in Koordinatendarstellung um:
in Normalenform in Koordinatendarstellung um:
 . Wir wählen günstigerweise als Normalenvektor
. Wir wählen günstigerweise als Normalenvektor  .
.
Dann ist  .
.
Die Normalenform der Ebenengleichung ist also  .
.
Setze nun  in diese Gleichung ein:
in diese Gleichung ein:
 ;
;
 ;
;
Das ist falsch. Also haben die beiden Ebenen keine gemeinsamen Punkte. Sie müssen deswegen echt parallel sein.
(2) Beschreibe die Lage von Ebene  und Ebene
und Ebene  zueinander und stelle gegebenenfalls eine Gleichung der Schnittgerade auf!
zueinander und stelle gegebenenfalls eine Gleichung der Schnittgerade auf!
Da die beiden Normalenvektoren  und
und  linear unabhängig sind, müssen sich die beiden Ebenen in einer Geraden schneiden.
linear unabhängig sind, müssen sich die beiden Ebenen in einer Geraden schneiden.
Die beiden Ebenengleichungen stellen ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten dar, es ist also unterbestimmt. Deswegen kann man eine Unbekannte frei wählen.
Wähle  . Die beiden Gleichungen sind dann:
. Die beiden Gleichungen sind dann:
 und
und  .
.
 ;
;
 ;
;

Die Schnittgerade hat also die Gleichung  .
.
Die folgende Abbildung veranschaulicht die möglichen Lagen dreier Ebenen zueinander:
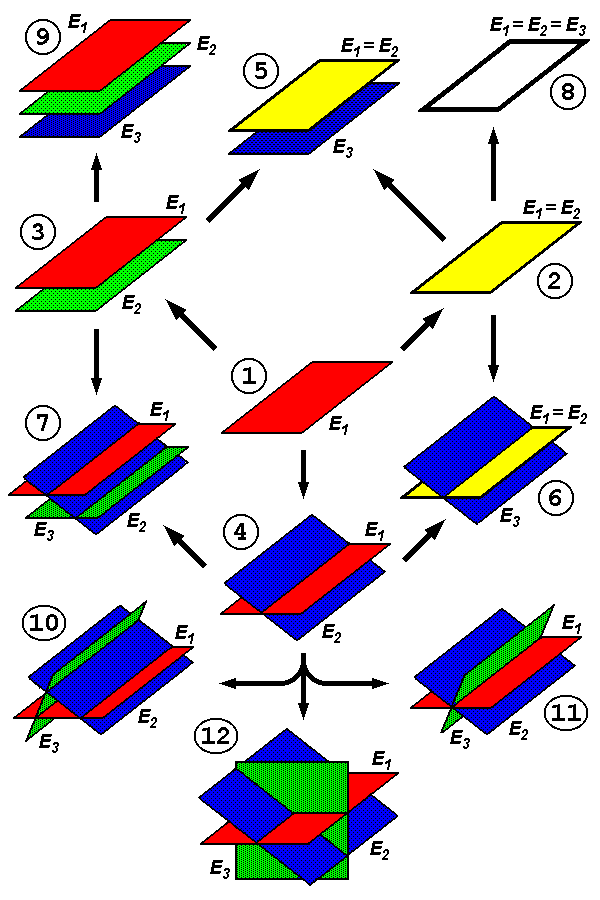
Lage zweier Ebenen bei lernzentrum.de
5.6 Abstandsbestimmungen
Abstand zweier Punkte:
Der Abstand  zweier Punkte
zweier Punkte  und
und  ist gleich dem Betrag des Verbindungsvektors
ist gleich dem Betrag des Verbindungsvektors  :
:

|
Abstand eines Punktes von einer Geraden, Lotfußpunkt
Sei  ein Punkt außerhalb einer Geraden
ein Punkt außerhalb einer Geraden 
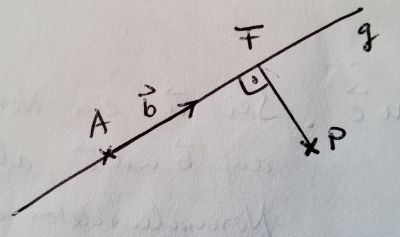
Für den Lotfußpunkt  muss dann gelten:
muss dann gelten:  und
und  .
.
Aus diesen zwei Bedingungen kann man den Lotfußpunkt berechnen und damit den gesuchten Abstand

|
Welchen Abstand hat der Punkt  von der Gerade
von der Gerade  ?
?
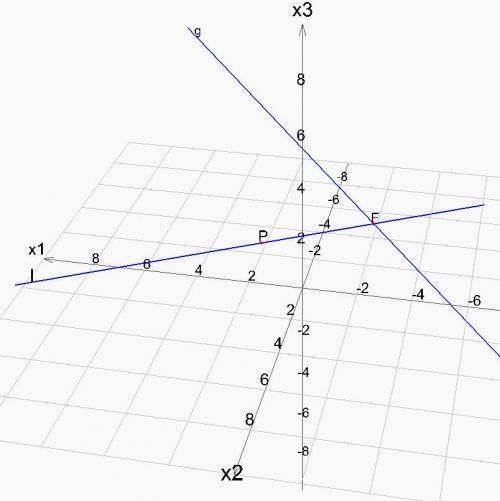
Sei  der gesuchte Lotfußpunkt (vom Punkt
der gesuchte Lotfußpunkt (vom Punkt  aus) auf der Gerade
aus) auf der Gerade  . Damit gilt:
. Damit gilt:  ;
;
 ;
;
 ;
;  ;
;  ;
;
 ;
;
Abstand zweier paralleler Geraden
Man berechnet wie im letzten Abschnitt den Abstand eines Punktes der einen Gerade von der anderen Gerade.
Abstand eines Punktes von einer Ebene
Man erhält den Abstand eines Punktes  von einer Ebene
von einer Ebene  , wenn man den Ortsvektor
, wenn man den Ortsvektor  des Punktes in die linke Seite der Hesse'schen Normalenform der Ebene einsetzt:
des Punktes in die linke Seite der Hesse'schen Normalenform der Ebene einsetzt:

|
Ist dabei  , so liegen der Ursprung des Koordinatensystems und der Punkt
, so liegen der Ursprung des Koordinatensystems und der Punkt  auf verschiedenen Seiten von der Ebene aus gesehen.
auf verschiedenen Seiten von der Ebene aus gesehen.
Ist dabei  , so liegen der Ursprung und der Punkt
, so liegen der Ursprung und der Punkt  auf derselben Seite von der Ebene aus gesehen.
auf derselben Seite von der Ebene aus gesehen.
Welchen Abstand haben der Ursprung und der Punkt  von der Ebene
von der Ebene  ?
?
Normalenvektor der Ebene ist  . Der Einheitsvektor dazu ist
. Der Einheitsvektor dazu ist  .
.
Dann ist  .
.
Wähle deshalb für die HNF den Normaleneinheitsvektor  . Damit ist
. Damit ist  .
.
Die skalare HNF der Ebenengleichung ist also:  .
.
Die gesuchten Abstände erhält man nun einfach durch Einsetzen der Koordinaten der Punkte:
 ;
;
 ; (Der Ursprung des Koordinatensystems und der Punkt
; (Der Ursprung des Koordinatensystems und der Punkt  liegen auf verschiedenen Seiten von der Ebene aus gesehen.)
liegen auf verschiedenen Seiten von der Ebene aus gesehen.)
Abstand zweier windschiefer Geraden
Gegeben sind zwei windschiefe Geraden: 
Gesucht ist der Abstand 
wobei  der Fußpunkt auf der Geraden
der Fußpunkt auf der Geraden  und
und  der Fußpunkt auf der Geraden
der Fußpunkt auf der Geraden  bezüglich des gemeinsamen Lotes der beiden Geraden ist:
bezüglich des gemeinsamen Lotes der beiden Geraden ist:
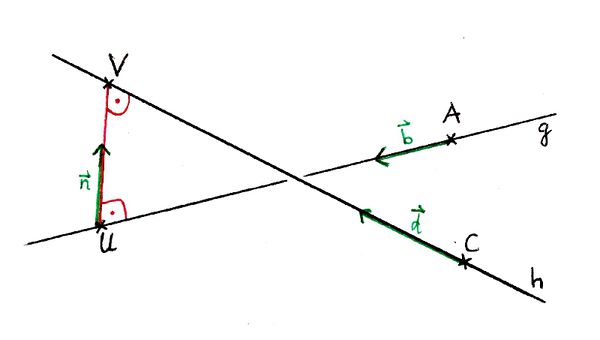
Es muss dabei für den gemeinsamen Normalenvektor  gelten:
gelten:

Man bildet eine geschlossene Vektorkette:

Mit  und nach Skalarproduktbildung mit
und nach Skalarproduktbildung mit  auf beiden Seiten der Gleichung ergibt sich:
auf beiden Seiten der Gleichung ergibt sich:

Mit  vereinfacht sich dies zu:
vereinfacht sich dies zu:

Daraus erhält man leicht  und damit
und damit  und somit auch den gesuchten Abstand
und somit auch den gesuchten Abstand 








Alternativ kann man den Abstand zweier windschiefer Geraden  und
und  auch miitels einer Hilfsebene
auch miitels einer Hilfsebene  bestimmen, die die Gerade
bestimmen, die die Gerade  enthält und zur anderen Gerade
enthält und zur anderen Gerade  parallel ist.
parallel ist.
Der Abstand der windschiefen Geraden ist dann gleich dem Abstand des Aufpunktes der Geraden  von der Ebene
von der Ebene  .
.
5.7 Schnittwinkel
Schnittwinkel zweier Geraden
Der Schnittwinkel zweier Geraden ist der Zwischenwinkel zwischen den beiden zugehörigen Richtungsvektoren der beiden Geraden.
Schnittwinkel zwischen Gerade und Ebene
Sei  der Richtungsvektor der Geraden und
der Richtungsvektor der Geraden und  ein Normalenvektor der Ebene.
ein Normalenvektor der Ebene.
Dann gilt für den Schnittwinkel  zwischen Gerade und Ebene:
zwischen Gerade und Ebene:

|
Wie groß ist der Schnittwinkel der Geraden  mit der Ebene
mit der Ebene  ?
?
 ;
;

Schnittwinkel zweier Ebenen
Der Schnittwinkel zweier Ebenen ist der Zwischenwinkel zwischen den beiden zugehörigen Normalenvektoren der beiden Ebenen.
Mathematik GWM5 GWM6 GWM7 GWM8 GWM9 SchulheftM5 SchulheftM6 SchulheftM10 SchulheftM11
 Kombinatorik - eine Übersicht zu kombinatorischen Grundproblemen
Kombinatorik - eine Übersicht zu kombinatorischen Grundproblemen




















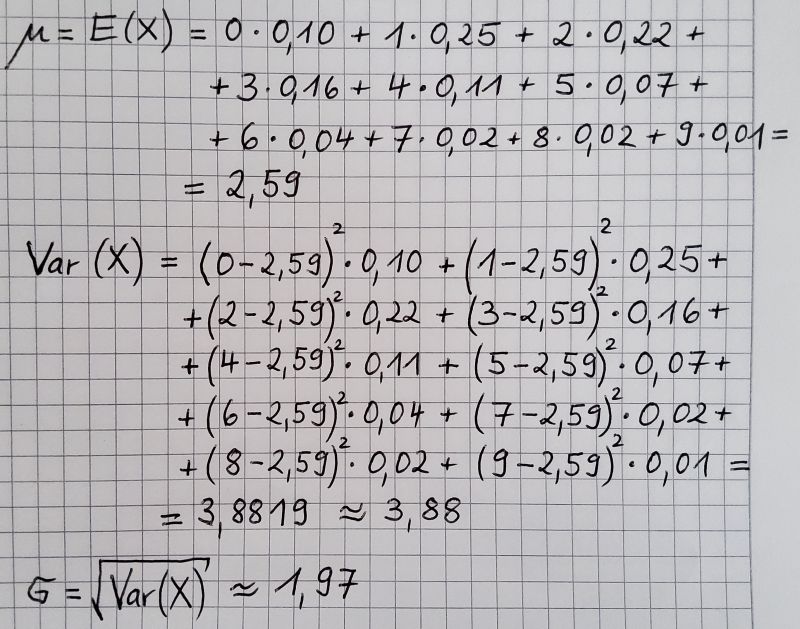

















































































































![{\displaystyle {\begin{pmatrix}1\\0\\2\end{pmatrix}}\circ \left[{\vec {x}}-{\begin{pmatrix}0\\-2\\2\end{pmatrix}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e784f1191510f53840e1ecf1746c2cca418bd09)









![{\displaystyle {\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\0\\2\end{pmatrix}}\circ \left[{\vec {x}}-{\begin{pmatrix}0\\-2\\2\end{pmatrix}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b95d16fcbe0e74009e30f133213f952e70f0ddae)