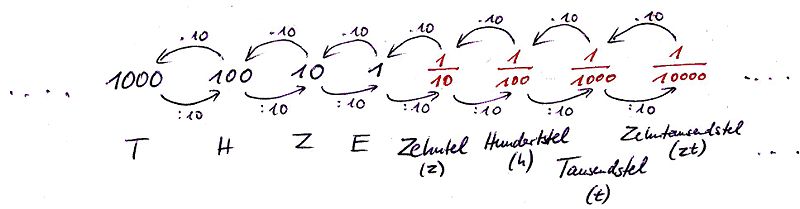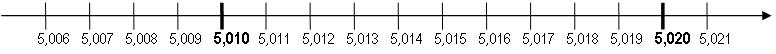SchulheftM6

^{Mathematik  GWM5  GWM6  SchulheftM5  SchulheftM10  SchulheftM11  SchulheftM12}

---

0. Wiederholung

siehe Grundwissen Mathematik 5

1. Rauminhalt (Volumen)

(zur Vorbereitung siehe Buch S. 130 und S. 131 "Volumen vergleichen und messen")

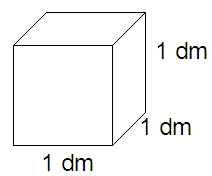
1.1 Die Volumeneinheit 1 dm³ ("Kubikdezimeter")

Ein Würfel der Kantenlänge 1 dm hat das Volumen 1 dm³ = 1 Liter.

1.2 Volumeneinheiten und ihre Umrechnung

Ein Würfel der Kantenlänge 1 mm hat das Volumen 1 mm³ ("Kubikmillimeter").

Ein Würfel der Kantenlänge 1 cm hat das Volumen 1 cm³ ("Kubikzentimeter").

Ein Würfel der Kantenlänge 1 m hat das Volumen 1 m³ ("Kubikmeter").

• Merke:

1 ml = 1 cm³ ("Milliliter");

1 hl = 100 l = 100 dm³ ("Hektoliter");

1 cl = 10 ml = 10 cm³ ("Zentiliter").

• Umrechnung:

Die Umrechnungszahl bei Volumeneinheiten ist 1000.

${\begin{matrix}1~m^{3}=1000~dm^{3};&1~dm^{3}=1000~cm^{3};&1~cm^{3}=1000~mm^{3};&\\&1~dm^{3}=0,001~m^{3};&1~cm^{3}=0,001~dm^{3};&1~mm^{3}=0,001~cm^{3};\end{matrix}}$

(Tipp: Das Umwandeln von Einheiten üben von A. Brünner)

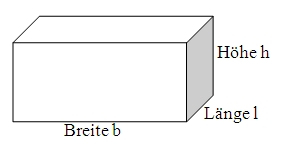
1.3 Volumen des Quaders

(Herleitung siehe Buch S. 137)

Das Volumen eines Quaders ist "Breite mal Länge mal Höhe":

$V_{Q}=b\cdot l\cdot h$

oder

$V_{Q}=G\cdot h$

mit G: Grundfläche.

Damit folgt speziell für das Volumen eines Würfels der Kantenlänge a:

$V_{W}=a\cdot a\cdot a=a^{3}$

(Tipp: Quaderrechner von A. Brünner)

2. Der Bruchbegriff

2.1 Grundlagen

Es gibt verschiedene Formen von Brüchen.

• echte Brüche: ${\frac {1}{2}};\ {\frac {3}{4}};\ {\frac {7}{16}};\ {\frac {99}{100}}$

• unechte Brüche: ${\frac {11}{4}};\ {\frac {3}{2}};\ {\frac {888}{88}};\ {\frac {7}{2}}$

• gemischte Brüche: $1{\frac {1}{2}};\ 2{\frac {3}{4}};\ 17{\frac {9}{11}}$

• Dezimalbrüche: $0,33;\ 4,39;\ 1,25;\ 2,5$

Ein echter und ein unechter Bruch besteht aus einer Zahl oberhalb des Bruchstrichs (Zähler) und einer Zahl unterhalb des Bruchstrichs (Nenner).

${\frac {\mathrm {Z{\ddot {a}}hler} }{\mathrm {Nenner} }}$

Bei einem echten Bruch ist der Zähler immer kleiner als der Nenner.

Bei gleichem Zähler gilt: Je größer der Nenner, desto kleiner ist der Wert des Bruches und umgekehrt.

${\frac {1}{6}}<{\frac {1}{5}}<{\frac {1}{4}}<{\frac {1}{3}}$

Der Nenner gibt an, aus wie vielen Teilen das Ganze besteht.

Der Zähler gibt an, wie viele dieser Teile den Bruchteil ausmachen.

Anteile werden mit Bruchzahlen oder häufig auch in Prozentschreibweise angegeben: $35\%={\frac {35}{100}}$ .

Das Prozentzeichen "%" deutet den Nenner 100 an.

Begriffe:

${\begin{matrix}{\frac {3}{11}}&von&88~Schrauben&sind&24~Schrauben\\\mathrm {Anteil} &&\mathrm {Ganzes} &&\mathrm {Bruchteil} \end{matrix}}$

Rechnerische Bestimmung des Bruchteils

Beispiel: ${\frac {3}{8}}$ von 24 Luftballons;

${\frac {3}{8}}\ \mathrm {von} \ 24=(24:8)\cdot 3=3\cdot 3=9$;

Rechnerische Bestimmung des Anteils

Beispiel: 75 Liter von einem Hektoliter;

$75~l\ \mathrm {von} \ 100~l={\frac {75}{100}}={\frac {3}{4}}$;

Rechnerische Bestimmung des Ganzen

Beispiel: ${\frac {3}{4}}$ von $x$ sind $201~Euro$;

$x=(201~Euro:3)\cdot 4=67~Euro\cdot 4=268~Euro$;

2.2 Brüche am Zahlenstrahl

Alle Brüche, die zum selben Punkt auf dem Zahlenstrahl gehören, haben trotz unterschiedlicher Schreibweise den gleichen Wert, der diese Bruchzahl bestimmt.

Bezeichnungen

Die Menge aller positiven Bruchzahlen mit Null wird mit $\mathbb {Q} _{0}^{+}$ ("Q Null plus") bezeichnet.

Brüche mit dem Zähler 1 heißen Stammbrüche, z.B. ${\frac {1}{7}},\ {\frac {1}{13}},\ {\frac {1}{20}},\ {\frac {1}{33}},\ {\frac {1}{457}},\ ...$.

Brüche, deren Zähler kleiner als ihr Nenner ist, heißen echte Brüche, z.B. ${\frac {3}{4}},\ {\frac {5}{7}},\ {\frac {6}{8}},\ {\frac {4}{9}},\ {\frac {12}{19}},\ ...$.

Echte Brüche sind zwischen 0 und 1 auf dem Zahlenstrahl.

Brüche, der Zähler größer als ihr Nenner ist, heißen unechte Brüche, z.B. ${\frac {4}{3}},\ {\frac {7}{5}},\ {\frac {9}{6}},\ {\frac {17}{11}},\ {\frac {74}{13}},\ ...$.

Unechte Brüche sind größer als 1.

Brüche, die den Wert einer ganzen Zahl haben, heißen Scheinbrüche, z.B. ${\frac {3}{3}},\ {\frac {5}{5}},\ {\frac {8}{4}},\ {\frac {24}{6}},\ {\frac {56}{7}},\ ...$.

Ihr Zähler ist ein Vielfaches ihres Nenners.

2.3 Brüche als Quotienten

(zur Vorbereitung siehe Buch S. 18)

Jedem Quotienten $\ a:b$ ist der Bruch ${\frac {a}{b}}$ gleichwertig. Kurz:

$a:b={\frac {a}{b}}$

(wobei $a\in \mathbb {N} _{0},b\in \mathbb {N}$)

Beispiele: $\ {\frac {56}{7}}=56:7=8;\ {\frac {7}{8}}=7:8=0,875;$

2.4 Erweitern

Beispiele: ${\frac {1}{5}}={\frac {1\cdot 3}{5\cdot 3}}={\frac {3}{15}};$ („mit 3 erweitert“) und ${\frac {4}{13}}={\frac {4\cdot 7}{13\cdot 7}}={\frac {28}{91}};$ („mit 7 erweitert“)

Der Wert eines Bruches ändert sich nicht, wenn man Zähler und Nenner mit derselben Zahl multipliziert. Dieser Vorgang heißt Erweitern.

2.5 Kürzen

Beispiele: ${\frac {3}{15}}={\frac {3:3}{15:3}}={\frac {1}{5}}$ („mit 3 gekürzt“) und ${\frac {32}{44}}={\frac {32:4}{44:4}}={\frac {8}{11}}$ („mit 4 gekürzt“)

Der Wert eines Bruches ändert sich nicht, wenn man Zähler und Nenner durch dieselbe Zahl dividiert. Dieser Vorgang heißt Kürzen.

Das Kürzen ist die Umkehrung des Erweiterns mit derselben Zahl und umgekehrt!

Ein Bruch ist vollständig gekürzt, wenn Zähler und Nenner keine gemeinsamen Teiler mehr haben.

Beispiel: ${\frac {210}{315}}={\frac {70}{105}}={\frac {10}{15}}={\frac {2}{3}}$

Brüche, die durch Kürzen oder Erweitern auseinander hervorgehen, haben den gleichen Wert!

2.6 Größenvergleich von Brüchen

Bei Brüchen mit gleichem Nenner ist derjenige größer, der den größeren Zähler hat.

Beispiele: ${\frac {7}{11}}>{\frac {4}{11}};\ {\frac {8}{27}}<{\frac {12}{27}}$

Bei Brüchen mit gleichem Zähler ist derjenige größer, der den kleineren Nenner hat.

Beispiele: ${\frac {7}{15}}>{\frac {7}{16}};\ {\frac {22}{29}}<{\frac {22}{25}}$

Brüche mit verschiedenen Nennern bringt man vor dem Größenvergleich auf einen gemeinsamen Nenner!

Den kleinsten gemeinsamen Nenner findet man, indem man das kleinste gemeinsame Vielfache (kgV) der Nenner bestimmt. Dieser Nenner heißt Hauptnenner.

3. Rechnen mit Bruchzahlen

3.1 Addition und Subtraktion von Brüchen

Brüche mit gleichem Nenner

Beispiele: ${\frac {7}{8}}+{\frac {1}{8}}={\frac {8}{8}}=1;\ {\frac {19}{16}}-{\frac {12}{16}}={\frac {7}{16}};\$

${\frac {a}{c}}\pm {\frac {b}{c}}={\frac {a\pm b}{c}}$

Man addiert bzw. subtrahiert Brüche mit gleichem Nenner, indem man als Zähler die Zähler addiert bzw. subtrahiert und als Nenner den gemeinsamen Nenner beibehält.

Brüche mit verschiedenen Nennern

Beispiele: ${\frac {4}{7}}+{\frac {12}{14}}={\frac {8}{14}}+{\frac {12}{14}}={\frac {20}{14}}={\frac {10}{7}};\ {\frac {12}{13}}-{\frac {31}{39}}={\frac {36}{39}}-{\frac {31}{39}}={\frac {5}{39}};\$

Brüche mit verschiedenen Nennern werden vor dem Addieren bzw. Subtrahieren auf den gleichen Nenner (günstig: Hauptnenner) gebracht!

Gemischte Zahlen

Terme wie $2+{\frac {3}{8}}$ schreibt man oft auch einfacher $2{\frac {3}{8}}$ und nennt solche Zahlen gemischte Zahlen.

Tipp: Zum Rechnen die gemischten Zahlen in unechte Brüche umwandeln!

Zur Umwandlung:

$7{\frac {3}{14}}={\frac {7\cdot 14+3}{14}}={\frac {101}{14}};\ \ {\frac {131}{15}}=131:15\ (=8\ Rest\ 11)=8{\frac {11}{15}}$

3.2 Multiplikation von Brüchen

Beispiele: ${\frac {1}{2}}\cdot {\frac {7}{4}}={\frac {7}{8}};\ {\frac {4}{3}}\cdot {\frac {3}{4}}={\frac {12}{12}}=1;\ {\frac {3}{7}}\cdot {\frac {12}{11}}={\frac {36}{77}};\$

${\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {a\cdot c}{b\cdot d}}$

Man multipliziert Brüche, indem man als Zähler die Zähler multipliziert und als Nenner die Nenner multipliziert.

Tipp: Erst Kürzen, dann Ausmultiplizieren!

Beispiele: ${\frac {1}{2}}\cdot 5={\frac {5}{2}};\ 7\cdot {\frac {3}{4}}={\frac {21}{4}};\ {\frac {3}{7}}\cdot 12={\frac {36}{7}};\$

$a\cdot {\frac {b}{c}}={\frac {a\cdot b}{c}}$

${\frac {a}{b}}\cdot c={\frac {a\cdot c}{b}}$

Man multipliziert einen Bruch mit einer ganzen Zahl, indem man als Zähler den Zähler mit der ganzen Zahl multipliziert und als Nenner den Nenner beibehält.

3.3 Division von Brüchen

Division von Brüchen mit gleichem Nenner

Beispiele: ${\frac {7}{12}}:{\frac {1}{12}}=7:1=7;\ {\frac {9}{11}}:{\frac {3}{11}}=9:3=3;\ {\frac {198}{17}}:{\frac {18}{17}}=198:18=11;\$

${\frac {a}{b}}:{\frac {c}{b}}=a:c$

Brüche mit gleichem Nenner werden dividiert, indem man ihre Zähler dividiert.

Division von Brüchen mit verschiedenen Nennern

Beispiele: ${\frac {3}{4}}:{\frac {5}{7}}={\frac {3\cdot 7}{4\cdot 7}}:{\frac {5\cdot 4}{7\cdot 4}}={\frac {21}{28}}:{\frac {20}{28}}=21:20={\frac {21}{20}}={\frac {3\cdot 7}{4\cdot 5}}={\frac {3}{4}}\cdot {\frac {7}{5}};\$

${\frac {11}{7}}:{\frac {9}{5}}={\frac {11\cdot 5}{7\cdot 5}}:{\frac {9\cdot 7}{5\cdot 7}}={\frac {55}{35}}:{\frac {63}{35}}=55:63={\frac {55}{63}}={\frac {11\cdot 5}{7\cdot 9}}={\frac {11}{7}}\cdot {\frac {5}{9}};\$

${\frac {a}{b}}:{\frac {c}{d}}={\frac {a\cdot d}{b\cdot d}}:{\frac {c\cdot b}{d\cdot b}}=(a\cdot d):(c\cdot b)={\frac {a\cdot d}{b\cdot c}}={\frac {a}{b}}\cdot {\frac {d}{c}};\$

${\frac {a}{b}}:{\frac {c}{d}}={\frac {a}{b}}\cdot {\frac {d}{c}}$

Man dividiert durch einen Bruch, indem man mit seinem Kehrbruch multipliziert!

Doppelbrüche

${\frac {\quad {\frac {a}{b}}\quad }{\quad {\frac {c}{d}}\quad }}={\frac {a}{b}}:{\frac {c}{d}}={\frac {a}{b}}\cdot {\frac {d}{c}}$

Der Hauptbruchstrich bedeutet auch "geteilt durch" und wirkt wie Klammern um Zähler und Nenner.

(Tipps: Bruchrechnen und Dezimalzahlen bei Serlo, Trainingsprogramm Bruchrechnen von W. Fendt oder Grundrechenarten bei Brüchen von A. Brünner)

4. Dezimalbrüche

Beispiele: 2,99 €; 0,49 €; Notendurchschnitt 3,46; 0,33 l; 5,22 km; 0,004 m;

4.1 Grundlagen

Eine Zahl in dieser "Komma-Darstellung" nennt man Dezimalbruch oder Dezimalzahl.

Stufenzahlen

Stellenwerttafel

ZT	T	H	Z	E	,	z	h	t	zt	ht	m
4	7	2	3	5	,	2
				0	,	1	7	5	8	9	4
		1	0	7	,	7	0	7	1

oder als gemischte Zahlen: $47235{\frac {2}{10}};\ {\frac {175894}{1000000}};\ 10{\frac {7071}{10000}};$

4.2 Umwandlung zwischen Bruch und Dezimalbruch

Wichtige Dezimalbrüche

${\frac {1}{10}}=0,1$	${\frac {1}{100}}=0,01$	${\frac {1}{1000}}=0,001$
${\frac {1}{2}}=0,5$	${\frac {1}{3}}=0,333...$	${\frac {1}{4}}=0,25$
${\frac {3}{4}}=0,75$	${\frac {1}{5}}=0,20$	${\frac {1}{8}}=0,125$
${\frac {3}{8}}=0,375$	${\frac {5}{8}}=0,625$	${\frac {7}{8}}=0,875$

Umwandlung

Ein Bruch ${\frac {z}{n}}$ lässt sich in einen Dezimalbruch umwandeln, indem der Quotient $z:n$ berechnet wird. Beim Auftreten des ersten Restes wird im Ergebnis das Komma gesetzt.

4.3 Dezimalbrüche an der Zahlengeraden

Beispiele:

4.4 Runden

Beim Runden eines Dezimalbruchs auf eine bestimmte Stelle muss man die nächste Stelle rechts davon betrachten und bei 0, 1, 2, 3 oder 4 abrunden bzw. bei 5, 6, 7, 8 oder 9 aufrunden.

Beispiele:

Auf Zehntel gerundet: $3,427\approx 3,4;\quad 3,0483\approx 3,0;\quad 1,70789\approx 1,7$

Auf Hunderstel gerundet: $3,429\approx 3,42;\quad 3,0493\approx 3,05;\quad 1,7489\approx 1,75$

Auf Tausendstel gerundet: $3,4292\approx 3,429;\quad 3,0495\approx 3,050;\quad 1,7489\approx 1,749$

Geltende Ziffern eines Dezimalbruchs sind alle Ziffern außer den Vornullen.

Beispiele:

1,34 ist auf drei geltende Ziffern angegeben. Auf zwei geltende Ziffern genau angegeben ist es 1,3.

0,00762 ist auf drei geltende Ziffern angegeben. Auf eine geltende Ziffern genau angegeben ist es 0,008.

-2,00892 ist auf sechs geltende Ziffern angegeben. Auf vier geltende Ziffern genau angegeben ist es -2,009.

Angabe, zwischen welchen Werten ein gerundeter Dezimalbruch liegt:

Beispiele: 6,195 ≦ 6,20 < 6,205; 9,995 ≦ 10,00 < 10,005; 0,10095 ≦ 0,1010 < 0,10105;

4.5 Addition und Subtraktion von Dezimalbrüchen

Beispiele: 4,4 + 2,7 = 7,1; 2,31 + 4,227 = 6,537; 7,7 - 3,9 = 3,8; 9,112 - 7,12 = 1,992;

Achte darauf, nur Stellen mit gleichem Stellenwert zusammenzufassen!

4.6 Multiplikation und Division von Dezimalbrüchen

Beispiele: 28,347 • 10 = 283,47; 28,347 • 100 = 2834,7; 28,347 • 1000 = 28347;

Ein Dezimalbruch wird mit einer Stufenzahl multipliziert, indem man das Komma um so viele Stellen nach rechts verschiebt, wie die Stufenzahl Nullen hat.

Beispiele: 2,347 : 10 = 0,2347; 2,347 : 100 = 0,02347; 2,347 : 1000 = 0,002347;

Ein Dezimalbruch wird durch eine Stufenzahl dividiert, indem man das Komma um so viele Stellen nach links verschiebt, wie die Stufenzahl Nullen hat.

Beispiele:

$1,7\cdot 8={\frac {17}{10}}\cdot 8={\frac {17\cdot 8}{10}}={\frac {136}{10}}=13,6;$

$4,27\cdot 3,4={\frac {427}{100}}\cdot {\frac {34}{10}}={\frac {427\cdot 34}{1000}}={\frac {14518}{1000}}=14,518;$

Zwei Dezimalbrüche werden miteinander multipliziert, indem man erst ohne Kommas multipliziert und anschließend im Ergebnis das Komma so setzt, dass die Summe der Anzahlen der Nachkommastellen die Anzahl der Nachkommastellen des Ergebnisses ist.

Beispiele:

513,24 : 1,2 = 5132,4 : 12 = 427,7; 23,10488 : 4,33 = 2310,488 : 433 = 5,336;

Bei der Division zweier Dezimalbrüche schiebt man beide Kommas um so viele Stellen nach rechts, bis der Divisor eine natürliche Zahl ist (entspricht dem Erweitern mit einer Stufenzahl).

4.7 Periodische Dezimalbrüche

Beispiele:

${\frac {1}{1}}=1;\ {\frac {1}{2}}=0,5;\ {\frac {1}{3}}=0,{\overline {3}};\ {\frac {1}{4}}=0,25;\ {\frac {1}{5}}=0,2;$

${\frac {1}{6}}=0,1{\overline {6}};\ {\frac {1}{7}}=0,{\overline {142857}};\ {\frac {1}{8}}=0,125;\ {\frac {1}{9}}=0,{\overline {1}};\ {\frac {1}{10}}=0,1;$

${\frac {1}{11}}=0,{\overline {09}};\ {\frac {1}{12}}=0,08{\overline {3}};\ {\frac {1}{13}}=0,{\overline {076923}};\ {\frac {1}{14}}=0,0{\overline {714285}};\ {\frac {1}{15}}=0,0{\overline {6}};$

${\frac {1}{16}}=0,0625;\ {\frac {1}{17}}=0,{\overline {0588235294117647}};\ {\frac {1}{18}}=0,0{\overline {5}};\ {\frac {1}{19}}=0,{\overline {052631578947368421}};\ {\frac {1}{20}}=0,05;$

Wandelt man Brüche in Dezimalbrüche um, so ergibt sich ein

• endlicher Dezimalbruch ( ${\frac {1}{8}}=0,125$ ) oder
• unendlicher rein-periodischer Dezimalbruch ( ${\frac {1}{13}}=0,{\overline {076923}}$ ) oder
• unendlicher gemischt-periodischer Dezimalbruch ( ${\frac {1}{15}}=0,0{\overline {6}}$ ).

Enthält der Nenner des vollständig gekürzten Bruches nur die Primfaktoren 2 und 5, so ist der zugehörige Dezimalbruch endlich.

Besonderheit:

${\frac {1}{9}}=0,{\overline {1}};\ {\frac {5}{9}}=0,{\overline {5}};$

${\frac {9}{9}}=0,{\overline {9}}=1;$

also: $0,4{\overline {9}}=0,5;\ 0,778{\overline {9}}=0,779;$

5. Zufallsexperimente, absolute und relative Häufigkeit

Zufallsexperimente

Zufallsexperimente sind unter gleichen Bedingungen wiederholbare Vorgänge, deren Ergebnisse nicht voraussagbar sind.

Beispiele: Münzwurf, Würfeln, Losen

Häufigkeiten

Beispiel:

Lena hat bei 30 Versuchen fünf mal eine Sechs gewürfelt.
Markus hat bei 20 Versuchen vier mal eine Sechs gewürfelt.

Die absolute Häufigkeit für eine Sechs beträgt bei Lena 5 und bei Markus 4.

Zum sinnvollen Vergleichen der Ergebnisse müssen die Gesamtzahlen mit berücksichtigt werden.

Markus: ${\frac {4}{20}}={\frac {1}{5}}=20\%$

Lena: ${\frac {5}{30}}={\frac {1}{6}}=16,{\overline {6}}\%$

Lena hat zwar einmal häufiger die Sechs gewürfelt, dafür aber auch mehr Würfe benötigt.
Man unterscheidet zwischen absoluter (lat. losgelöst) und relativer (lat. auf etwas bezogen) Häufigkeit des Ereignisses Sechs.

Die Anzahl mit der ein bestimmtes Ereignis auftritt heißt absolute Häufigkeit.
Dividiert man die absolute Häufigkeit eines Ergeignisses durch die Gesamtzahl der Durchführungen des Zufallsexperiments, so erhält man die relative Häufigkeit.

Empirisches Gesetz der großen Zahlen

Das empirische Gesetz der großen Zahlen besagt, dass sich die relative Häufigkeit eines Ergebnisses eines Zufallsexperiments mit zunehmender Anzahl der Durchführungen um einen bestimmten Wert stabilistiert. Dieser durch Erfahrung gewonnene Wert kann als Wahrscheinlichkeit für dieses Ergebnis interpretiert werden.

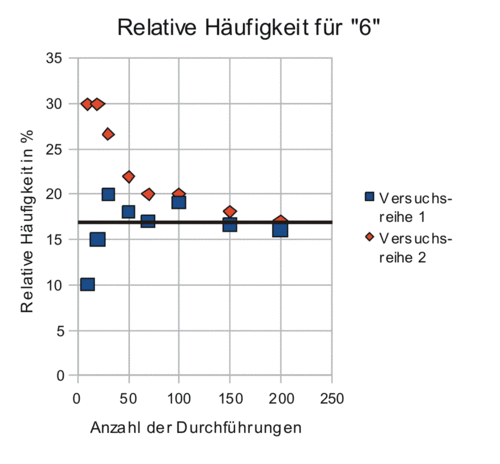
Beispiel: Untersuchung der relativen Häufigkeit für das Würfeln einer "6" mit einem Spielwürfel

Anzahl der Durchführungen	10	20	30	50	70	100	150	200
Relative Häufigkeit von "6" in % (1. Versuchsreihe)	10	15	20	18	17	19	16,7	16
Relative Häufigkeit von "6" in % (2. Versuchsreihe)	30	30	26,7	22	20	20	18	17

Die relative Häufigkeit für "6" pendelt sich mit zunehmender Anzahl von Durchführungen um ${\frac {1}{6}}=16,{\overline {6}}\%$ ein.
Man kann diesen experimentell ermittelten Wert als Wahrscheinlichkeit dafür interpretieren, bei einem Wurf eine "6" zu würfeln.

6. Prozentrechnen

Prozentangaben und Kreisdiagramme

Die Verteilung einer Gesamtmenge kann mit einem Kreisdiagramm veranschaulicht werden. Um die Größe eines Kreissektors festzulegen, muss zum entsprechenden Anteil der Winkel berechnet werden.

1 % entspricht 3,6°

12 % entsprechen 12  $\ \cdot$  3,6° = 43,2°

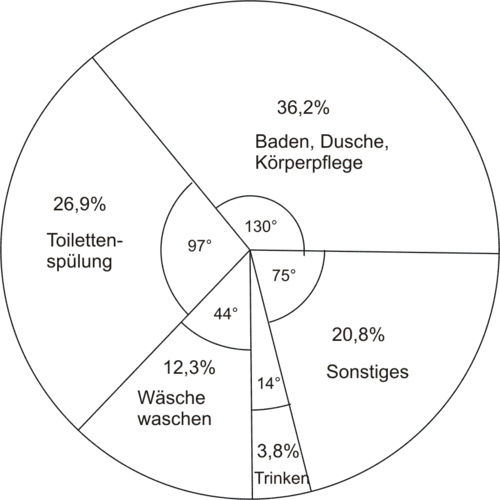
Bsp.: Anteile des täglichen Wasserverbrauchs im Haushalt

• Körperpflege 47 l
  36,2 %

• Toilettenspülung 35 l
  26,9 %

• Wäsche waschen 16 l
  12,3 %

• Trinken, Kochen 5 l
  3,8 %

• Sonstiges 27 l
  20,8 %

Berechnung des Prozentwertes

Bsp.: 20 % von 350 Euro

20 % $\cdot$ 350 € = 0,20 $\cdot$ 350 € = 70 €

Analog zur Berechnung von Bruchteilen eines Ganzen (vgl. 2.1) werden Fachbegriffe verwendet:

20 %: Prozentsatz

350 €: Grundwert (Wert, auf den die Prozentangabe bezogen wird)

70 €: Prozentwert

Der Prozentwert ergibt sich damit als Produkt von Prozentsatz und Grundwert.

$PW=PS\cdot GW$

Bei der Berechnung des Prozentwertes im Kopf ist oft die Anwendung des Dreisatzes hilfreich:

100 %	350 €
10 %	35 €
20 %	70 €

Berechnung des Prozentsatzes

Bsp.: 24 von 160

$24:160={\frac {24}{160}}={\frac {3}{20}}={\frac {15}{100}}=15\%$

24: Prozentwert

160: Grundwert

15 %: Prozentsatz

Der Prozentsatz ergibt sich als Quotient aus Prozentwert und Grundwert.

$PS={\frac {PW}{GW}}$

Berechnung des Grundwertes

Der Grundwert ist der Wert, auf den sich der Prozentsatz bezieht. Ihm entsprechen 100 %.

Bsp.: 72 % von ...ha sind 9 ha.

1. Weg: "Dreisatz"

72 %	9 ha
1 %	${\frac {9}{72}}ha=0,125ha$
100 %	12,5 ha

Antwort: 72 % von 12,5 ha sind 9 ha.

2. Weg: (durch "Umkehraufgabe")

...ha $\cdot$ 0,72 = 9 ha

folglich gilt:

9 ha : 0,72 = 12,5 ha

Den Grundwert berechnet man, indem man den Prozentwert durch den Prozentsatz dividiert.

$GW={\frac {PW}{PS}}$

7. Rationale Zahlen

7.1 Die Menge der rationalen Zahlen $\mathbb {Q}$

Die Menge aller Brüche heißt die Menge der rationalen Zahlen.

In ihr enthalten sind sowohl die natürlichen Zahlen, die ganzen Zahlen, die negativen Bruchzahlen, die positiven Bruchzahlen und auch die Null.

7.2 Rechnen mit den rationalen Zahlen

Es gelten die gleichen Rechenregeln, wie für das Rechnen mit den ganzen Zahlen.

8. Flächeninhalte

8.1 Fläche des Parallelogramms

Ein Parallelogramm kann in ein flächengleiches Rechteck verwandelt werden.

Maße des entstehenden Rechtecks:

Länge: eine Seitenlänge des Parallelogramms (Grundlinie)

Breite: Abstand der Grundlinie von der dazu parallelen Seite (Höhe)

Damit erhält man den Flächeninhalt des Parallelogramms, indem man die Grundlinie mit der zugehörigen Höhe multipliziert.

$A=a\cdot h_{a}=b\cdot h_{b}$

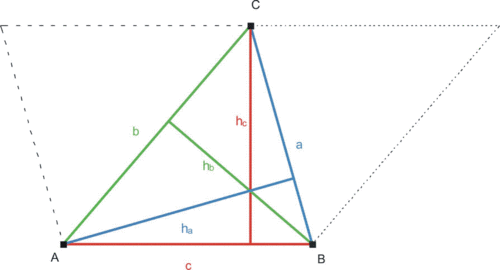
8.2 Fläche des Dreiecks

Ein Dreieck lässt sich mit einem flächengleichen Dreieck zu einem Parallelogramm ergänzen. Sein Flächeninhalt ist damit halb so groß, wie der des entstehenden Parallelogramms.

Den Flächeninhalt eines Dreiecks berechnet man, indem man das halbe Produkt aus der Länge einer Seite und der zugehörigen Höhe bildet. (Höhe: Abstand eines Eckpunktes von der gegenüberliegenden Seite)

$A={\frac {1}{2}}\cdot a\cdot h_{a}={\frac {1}{2}}\cdot b\cdot h_{b}={\frac {1}{2}}\cdot c\cdot h_{c}$

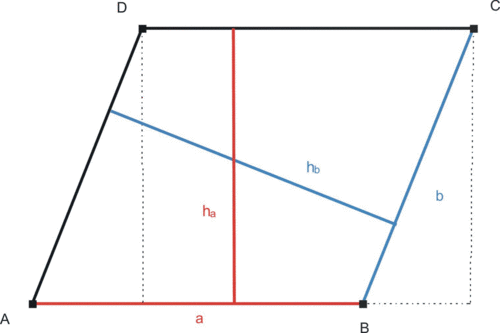
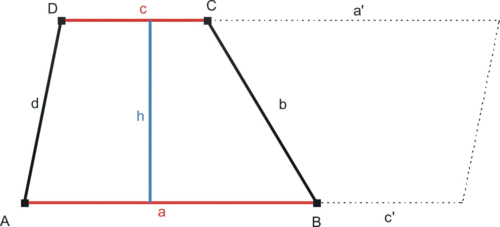
8.3 Fläche des Trapezes

Ein Trapez lässt sich durch ein weiteres flächengleiches Trapez zu einem Parallelogramm ergänzen. Sein Flächeninhalt ist damit halb so groß wie der des enstehenden Parallelogramms.

Den Flächeninhalt eines Trapezes berechnet man, indem man die Hälfte der Summe der parallelen Seiten mit dem Abstand der parallelen Seiten (Höhe) multipliziert.

$A={\frac {1}{2}}\cdot (a+c)\cdot h$

---

^{Mathematik  GWM5  GWM6  SchulheftM5  SchulheftM10  SchulheftM11  SchulheftM12}

---