GWM5

Grundwissen Mathematik 5. Klasse

GWM 5.1 Zahlenmengen

$\mathbb {N} =\{1,2,3,4,5,6,7,8,9,10,11,12,...\}$ Menge der natürlichen Zahlen

$\mathbb {N} _{0}=\{0,1,2,3,4,5,6,7,8,9,10,11,...\}$ Menge der natürlichen Zahlen mit Null

$\mathbb {Z} =\{...-4,-3,-2,-1,0,1,2,3,4,...\}$ Menge der ganzen Zahlen

Primzahlen: Eine Zahl die genau zwei Teiler hat, heißt Primzahl.

Menge der Primzahlen $=\{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,\$

$73,79,83,89,97,101,103,107,109,113,127,131,...\}\$

Primfaktorzerlegung: Jede Zahl lässt sich eindeutig in ein Produkt von Primzahlen zerlegen.

Beispiel: $60=2\cdot 30=2\cdot 2\cdot 15=2\cdot 2\cdot 3\cdot 5=2^{2}\cdot 3\cdot 5$

Menge der Quadratzahlen $=\{1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,\$

$324,361,400,441,484,529,576,625,...\}\$

Römische Zahlen: $I=1;\ V=5;\ X=10;\ L=50;\ C=100;\ D=500;\ M=1000$

$I,\ X,\ C,\ M$ dürfen bis zu dreimal nacheinander stehen. $I,\ X,\ C$ werden beim Voranstellen einmal abgezogen.

Beispiel: $MCMXCIV=1994;\ MMMDCCCLXXXVIII=3888$

GWM 5.2 Fachbegriffe beim Rechnen

Addition:

${\begin{matrix}171&+&19&=&190\\{\rm {1.\ Summand}}&+&{\rm {2.\ Summand}}&=&{\rm {Wert\ der\ Summe}}\end{matrix}}$

Subtraktion:

${\begin{matrix}190&-&19&=&171\\{\rm {Minuend}}&-&{\rm {Subtrahend}}&=&{\rm {Wert\ der\ Differenz}}\end{matrix}}$

Multiplikation:

${\begin{matrix}125&\cdot &8&=&1000\\{\rm {1.\ Faktor}}&\cdot &{\rm {2.\ Faktor}}&=&{\rm {Wert\ des\ Produkts}}\end{matrix}}$

Division:

${\begin{matrix}1000&:&8&=&125\\{\rm {Dividend}}&:&{\rm {Divisor}}&=&{\rm {Wert\ des\ Quotienten}}\end{matrix}}$

GWM 5.3 Potenzen

Potenz: $a\cdot a\cdot a\cdot a\cdot a\cdot a=a^{6}$

Beispiel: $4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4=4^{7}$

Merke: $2^{3}=8\$ aber $2\cdot 3=6$

Potenz:

${\begin{matrix}3^{5}&=&243\\{\rm {Basis}}^{\rm {Exponent}}&=&{\rm {Wert\ der\ Potenz}}\end{matrix}}$

GWM 5.4 Rechengesetze und die Bedeutung der Null

Reihenfolge: „Klammer vor Potenz vor Punkt vor Strich!“

Was noch nicht zum Rechnen dran ist, schreibt man unverändert an!

Kommutativgesetz:

$a\cdot b=b\cdot a\qquad 5\cdot 3=3\cdot 5$

$a+b=b+a\qquad 5+3=3+5$

Assoziativgesetz:

$(a+b)+c=a+(b+c)=a+b+c\qquad (2+3)+5=2+(3+5)=2+3+5$

$(a\cdot b)\cdot c=a\cdot (b\cdot c)=a\cdot b\cdot c\qquad (2\cdot 3)\cdot 5=2\cdot (3\cdot 5)=2\cdot 3\cdot 5$

Distributivgesetz:

$a\cdot (b+c)=a\cdot b+a\cdot c\qquad 2\cdot (5+3)=2\cdot 5+2\cdot 3$

$a\cdot (b-c)=a\cdot b-a\cdot c\qquad 2\cdot (5-3)=2\cdot 5-2\cdot 3$

$(a+b):c=a:c+b:c\qquad (170+51):17=170:17+51:17$

$(a-b):c=a:c-b:c\qquad (170-51):17=170:17-51:17$

Null bei der Multiplikation:

Ist ein Faktor Null, so ist auch der Produktwert Null. $3\cdot 0=0\cdot 3=0$

Ist der Produktwert Null, so muss mindestens ein Faktor Null sein!

Aus $a\cdot b=0$ folgt: $a=0\$ oder $\ b=0$.

Null bei der Division:

Allgemein: $0:a=0\quad (a\neq 0)\qquad 0:5=0$

Die Division durch Null ist nicht erlaubt!

GWM 5.5 Ganze Zahlen

Zahlengerade:

Betrag: Der Betrag einer Zahl ist ihre Entfernung vom Nullpunkt.

Beispiel: $|-4|=4;\ |4|=4$

Zahlen, die gleichen Betrag aber verschiedene Vorzeichen haben, heißen Gegenzahlen.

Beispiel: $4\leftrightarrow -4;\ 3\leftrightarrow -3$

GWM 5.6 Rechnen mit ganzen Zahlen: Addition und Subtraktion

$(+11)+(-4)=11-4=7\$

$(+11)-(+4)=11-4=7\$

$5+(+3)=5+3=8\qquad -5+(+3)=-5+3=-2$ $5+(-3)=5-3=2\qquad -5+(-3)=-5-3=-8$ $5-(+3)=5-3=2\qquad -5-(+3)=-5-3=-8$ $5-(-3)=5+3=8\qquad -5-(-3)=-5+3=-2$

GWM 5.7 Rechnen mit ganzen Zahlen: Multiplikation und Division

Regel: Gleiche Vorzeichen ergeben beim Multiplizieren und Dividieren "$+\$", ungleiche "$-\$".

$3\cdot (+5)=15\quad 15:(+5)=3\quad -3\cdot (+5)=-15\quad -15:(+5)=-3$

$3\cdot (-5)=-15\quad 15:(-5)=-3\quad -3\cdot (-5)=15\quad -15:(-5)=3$

GWM 5.8 Größen und Maßstab

Länge:

Umrechnungszahl $10\$, Ausnahme: $1~km=1000~m;\$

${\begin{matrix}1~m=10~dm;\quad \ &1~dm=10~cm;&1~cm=10~mm;\qquad \qquad \ \ \\1~m=0,001~km;&1~dm=0,1~m;&1~cm=0,1~dm=0,01~m;\end{matrix}}$

$1~mm=0,1~cm=0,01~dm=0,001~m;\$

Fläche:

Umrechnungszahl $100\$, Achtung: $1~km^{2}=1~km\cdot 1~km=1000~m\cdot 1000~m=1000000~m^{2}$

${\begin{matrix}1~km^{2}=100~ha;&1~ha=100~a;\quad \ \ &1~a=100~m^{2};\qquad \qquad \qquad \quad \\&1~ha=0,01~km^{2};&1~a=0,01~ha=0,0001~km^{2};\end{matrix}}$

${\begin{matrix}1~m^{2}=100~dm^{2};\qquad \qquad \quad &1~dm^{2}=100~cm^{2};&1~cm^{2}=100~mm^{2};\\1~m^{2}=0,01~a=0,0001~ha;&1~dm^{2}=0,01~m^{2};&1~cm^{2}=0,01~dm^{2};\end{matrix}}$

$1~mm^{2}=0,01~cm^{2};$

Masse:

Umrechnungszahl $1000\$

${\begin{matrix}1~t=1000~kg;&1~kg=1000~g;&1~g=1000~mg;&\\&1~kg=0,001~t;&1~g=0,001~kg;&1~mg=0,001~g;\end{matrix}}$

Zeit:

$1~a=365~d;\quad 1~d=24~h;\quad 1~h=60~min;\quad 1~min=60~s;$

Maßstab:

Der Maßstab $1:100\$ (lies 1 zu 100) bedeutet: $1~cm$ in der Zeichnung entspricht $100~cm$ in der Wirklichkeit.

Beispiel:

Eine $5~cm$ lange Strecke in einer Karte mit dem Maßstab $1:250000\$ entspricht in der Wirklichkeit $5\cdot 250000~cm=1250000~cm=12500~m=12,5~km$.

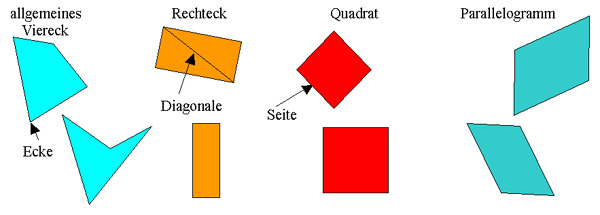
GWM 5.9 Kreis Vierecke

Alle Punkte, die von einem Punkt M aus gleich weit entfernt sind, liegen auf einem Kreis.

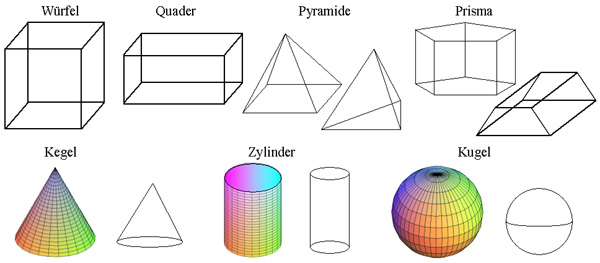
GWM 5.10 Körper

GWM 5.11 Umfang, Flächeninhalt, Oberflächen

Umfang des Rechtecks: $U_{R}=2\cdot (l+b)\qquad$	Umfang des Quadrates: $U_{Q}=4\cdot a$
Flächeninhalt des Rechtecks: $A_{R}=l\cdot b$	Flächeninhalt des Quadrates: $A_{Q}=a^{2}\$
Oberfläche des Quaders: $O_{Q}=2\cdot (l\cdot b+l\cdot h+b\cdot h)$	Oberfläche des Würfels: $O_{W}=6\cdot a^{2}\$

Netz des Quaders: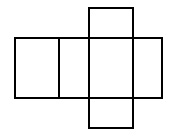

GWM 5.12 Strecken, Geraden, Winkel

Eine Strecke ist die kürzeste Verbindung zweier Punkte.

Die Schreibweise $[AB]\quad$ steht für die Strecke von A nach B.

Der Abstand von Anfangs- und Endpunkt ist die Länge der Strecke.

Mit der Schreibweise ${\overline {AB}}=5~cm\quad$ gibt man die Länge der Stecke an.

Verlängert man eine Strecke über einen Punkt bzw. über beide Punkte hinaus, so einsteht eine Halbgerade bzw. Gerade.

Beispiele:

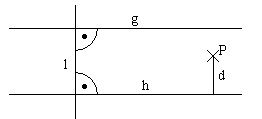
g ist parallel zu h: $g\|h$. g ist senkrecht zu l (g ist Lot zu l): $g\perp l$

Der Abstand d eines Punktes P von einer Geraden ist die Länge der senkrechten Verbindungsstrecke.

Zwei Halbgeraden mit demselben Anfangspunkt S teilen die Ebene in zwei Teile. Jeder Teil (mit Rand) heißt Winkel.

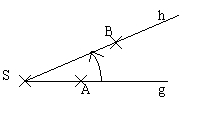
Bezeichnungen: $\angle (g,h)$ oder $\angle ASB$ oder kleine griechische Buchstaben:

$\alpha \$ alpha, $\beta \$ beta, $\gamma \$ gamma, $\delta \$ delta, $\epsilon \$ epsilon, $\eta \$ eta, $\vartheta \$ theta, $\mu \$ my, $\sigma \$ sigma, $\tau \$ tau, $\varphi \$ phi, $\omega \$ omega

Winkelarten:

• Nullwinkel: $\alpha =0^{o}$
• spitze Winkel: $0^{o}<\alpha <90^{o}$
• rechter Winkel: $\alpha =90^{o}$
• stumpfe Winkel: $90^{o}<\alpha <180^{o}$
• gestreckter Winkel: $\alpha =180^{o}$
• überstumpfe Winkel: $180^{o}<\alpha <360^{o}$

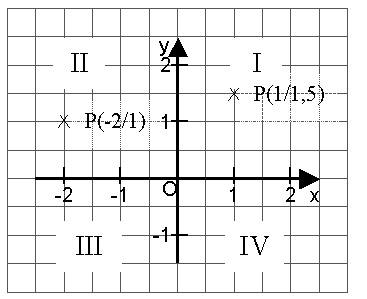
GWM 5.13 Koordinatensystem

Ein Koordinatensystem besteht aus zwei senkrechten Zahlenstrahlen mit gemeinsamem Nullpunkt. Die x-Achse heißt auch Abszisse, die y-Achse auch Ordinate.

Ein Punkt P(x/y) ist durch seine Koordinaten festgelegt.

Die Ebene wird in vier Quadranten unterteilt.

GWM 5.14 Zählprinzip, Baumdiagramm

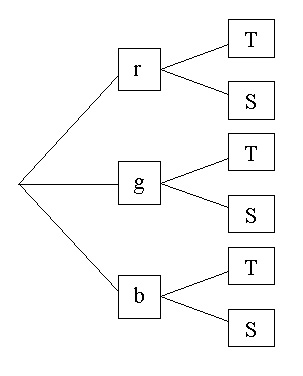
Veranschaulichung am Baumdiagramm:

Jeder Pfad durch den Baum steht für eine Kombinationsmöglichkeit.

Hat die erste Verzeigung $n\$ Äste und die zweite $m\$ Äste, so gibt es $n\cdot m$ Möglichkeiten.

Beispiel:

Es gibt rote (r), grüne (g) und blaue (b) Schuluniformen. Sie sind als T-Shirt T oder Sweatshirt S erhältlich. Es gibt $3\cdot 2=6$ Möglichkeiten, nämlich: rT, gT, bT, rS, gS, bS.

Web-Links

SMART-Aufgaben-Datenbank

---

Zurück zu Grundwissen Mathematik