SchulheftM11
Mathematik GWM5 GWM6 GWM7 GWM8 GWM9 SchulheftM5 SchulheftM6 SchulheftM10 SchulheftM12
Inhaltsverzeichnis
- 1 1. Graphen gebrochen rationaler Funktionen
- 2 2. Einführung in die Differentialrechnung
- 3 3. Anwendungen der Ableitung
- 4 4. GEOMETRIE: Koordinatengeometrie im Raum
- 5 5. Differentialrechnung: Weitere Ableitungsregeln
- 6 6. Natürliche Exponential- und Logarithmusfunktionen
- 7 7. STOCHASTIK: Wahrscheinlichkeit und Unabhängigkeit
- 8 8. Anwendungen der Differentialrechnung
1. Graphen gebrochen rationaler Funktionen
1.1 Verhalten in der Umgebung von Definitionslücken
Es gibt zwei Arten von Definitionslücken:
- Polstellen (--> senkrechte Asymptoten)
- Stetig hebbare Definitionslücken (--> "Loch" im Graphen)
1.2 Verhalten im Unendlichen
2. Einführung in die Differentialrechnung
2.1 Der Differenzenquotient (mittlere Änderungsrate)
Der Differenzenquotient entspricht der Steigung der Sekante durch die beiden Punkte des Graphen P(a|f(a)) und Q(b|f(b)).
2.2 Der Differentialquotient (lokale Änderungsrate)
Die Steigung des Graphen von f im Punkt P(x0|f(x0)) ist dieser Differentialquotient.
2.3 Die Ableitung
Bemerkung: h-Methode
Summenregel
Faktorregel
Produktregel
Quotientenregel
2.4 Stammfunktion
3. Anwendungen der Ableitung
3.1 Monotonie
3.2 Extrema (Extremstellen, Extremwerte)
3.3 Das Newton-Verfahren: Ein Iterationsverfahren zur Nullstellen-Bestimmung
Manchmal lassen sich die Nullstellen einer Funktion nicht durch einfaches Lösen der Gleichung finden.
Dann kann man mit Hilfe von numerischen Verfahren wenigstens einen Näherungswert für die Nullstellen ermitteln.
Solch ein Verfahren ist das Newton-Verfahren:
Hat eine differenzierbare Funktion eine Nullstelle, so kann man diese näherungsweise mit der Iteration
ermitteln. Dabei geht man von einem geeigneten Startwert aus.
ABER: Das Newton-Verfahren ist zwar für jede differenzierbare Funktion anwendbar, führt aber nicht immer zum Erfolg!
Newtonverfahren von xhochnde bei YouTube.com
Newton-Verfahren von Hannes Mitterlehner bei GeoGebra
Der Newton-Algorithmus zur Approximation von Nullstellen bei arndt-bruenner.de
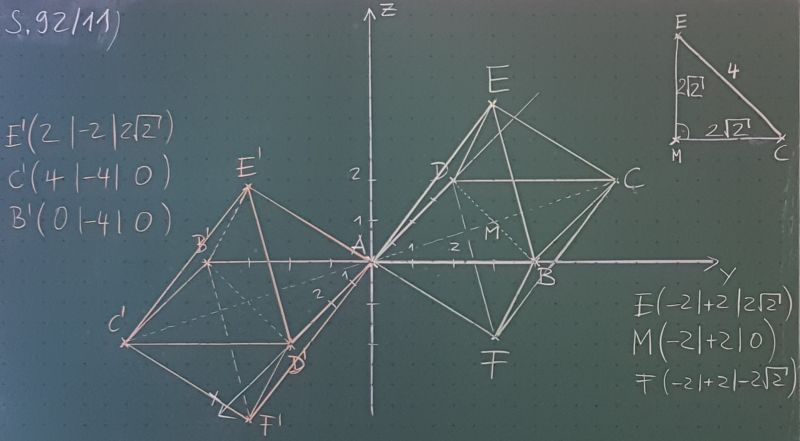
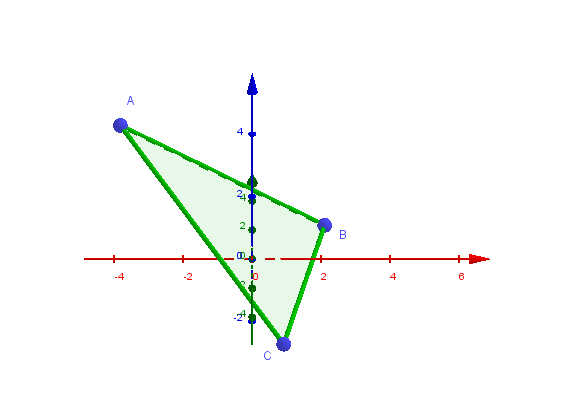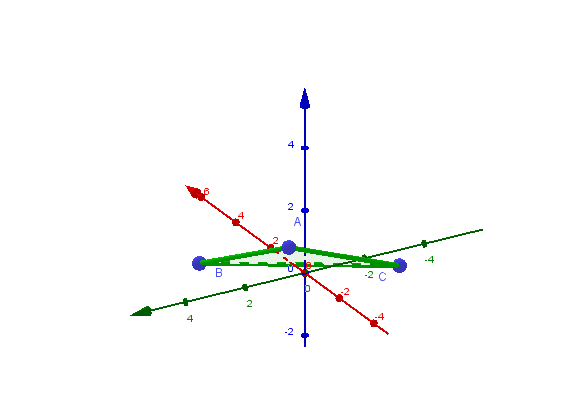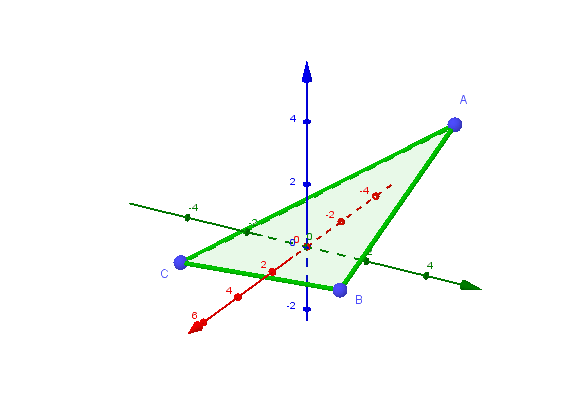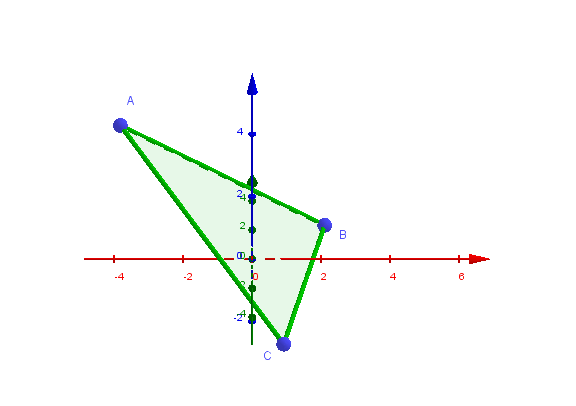
4. GEOMETRIE: Koordinatengeometrie im Raum
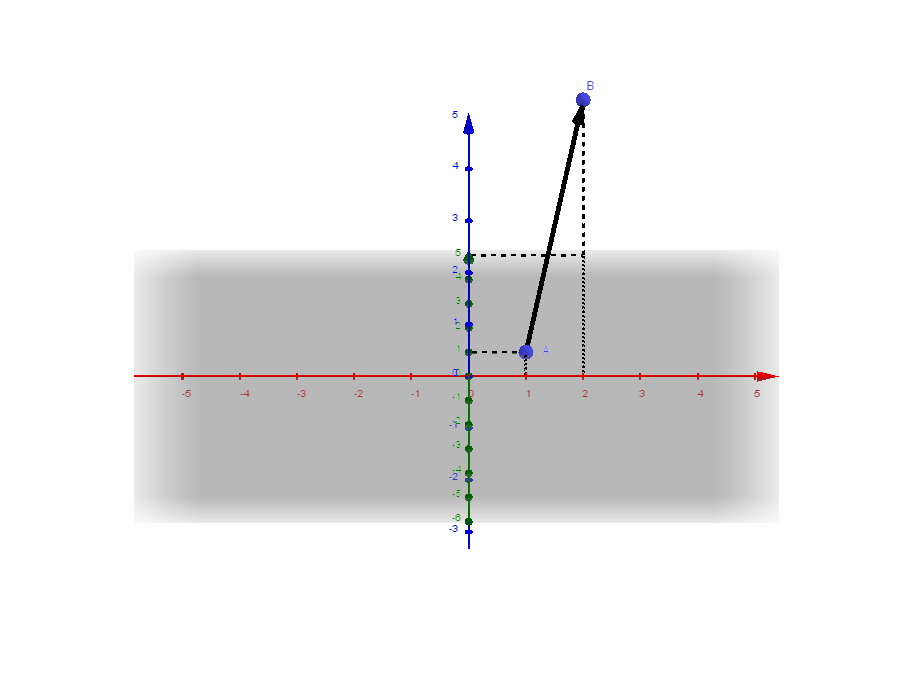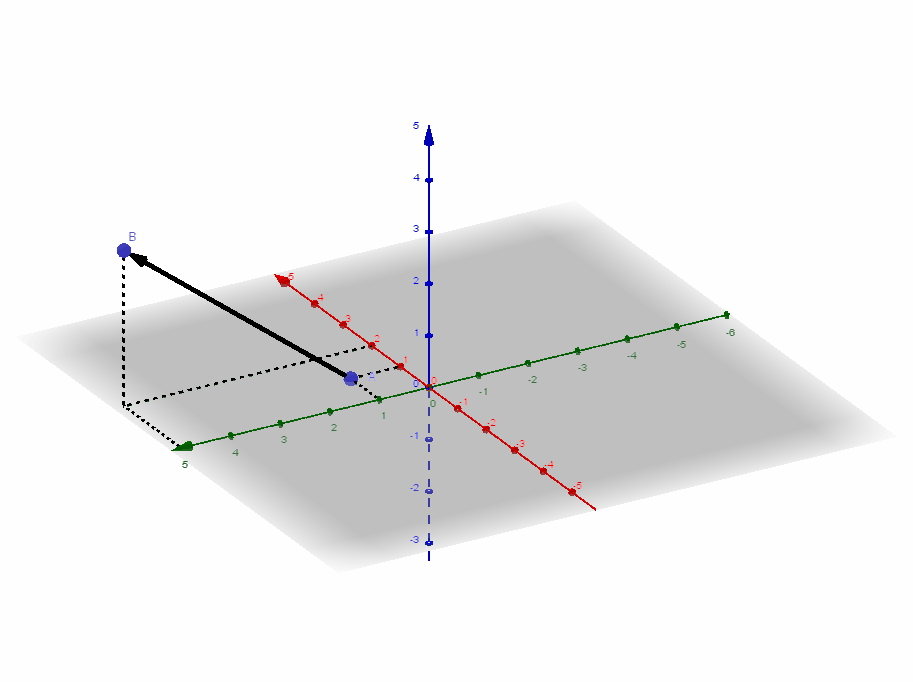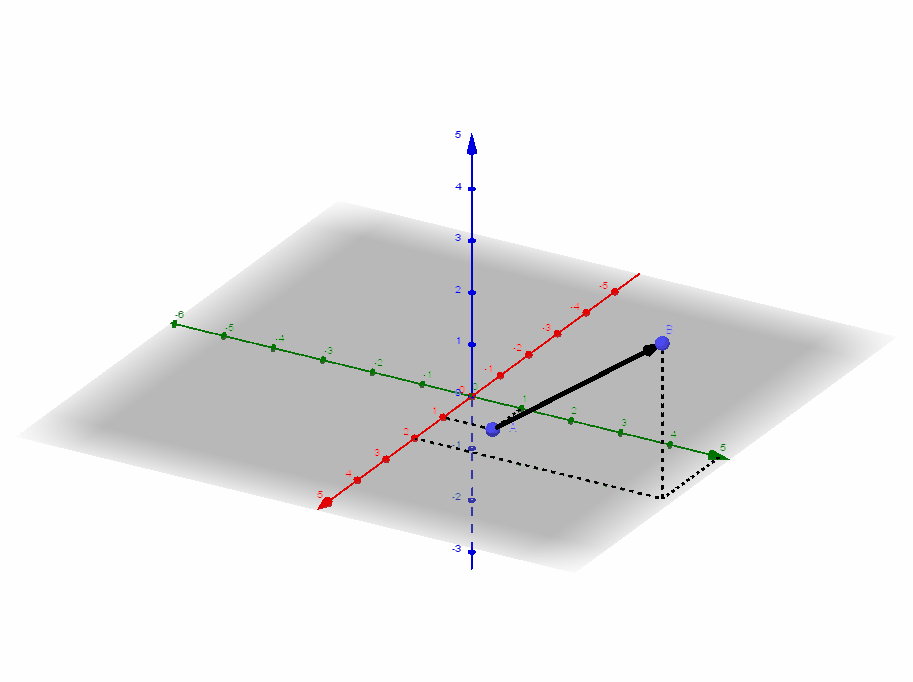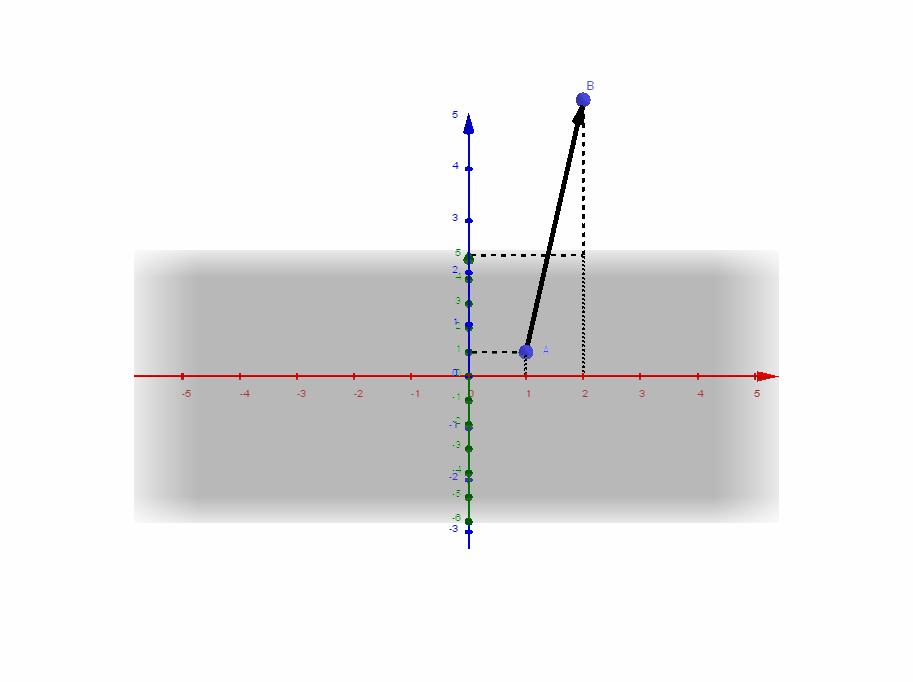
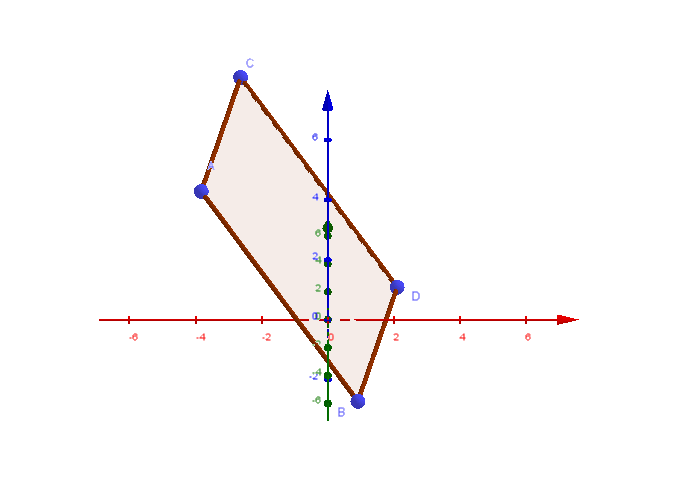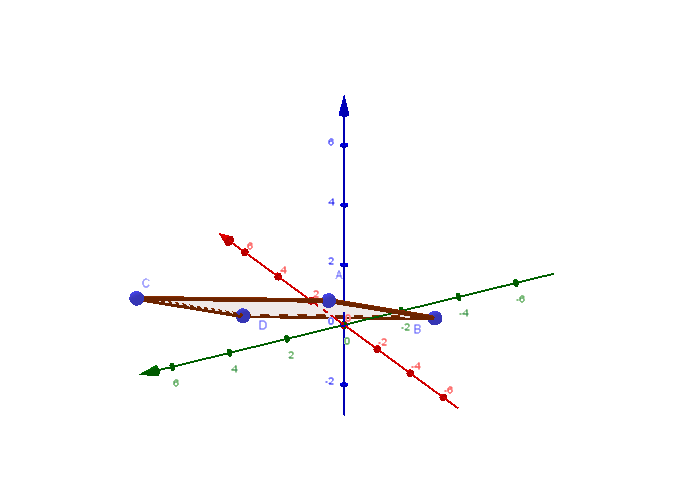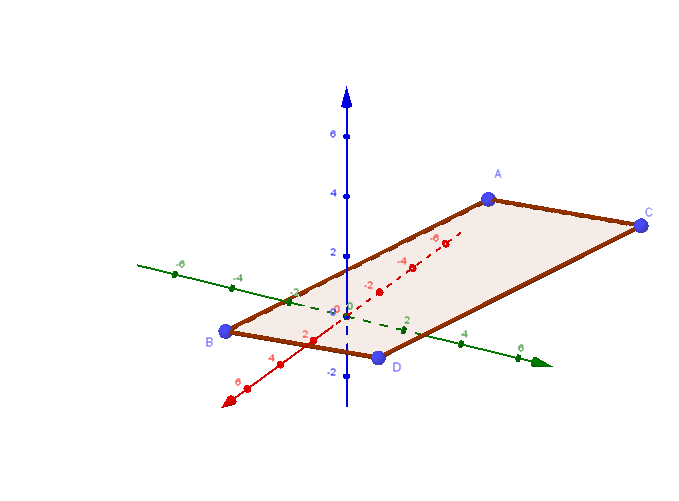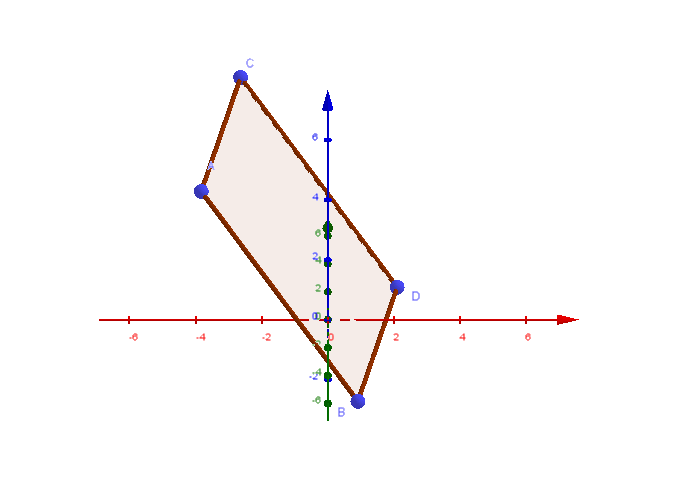
4.1 Das dreidimensionale Koordinatensystem
Zeichnen im 3D-Koordinatensystem bei Serlo Mathematik de.serlo.org
(Siehe auch 3D-Koordinatensystem von Dr. Marie-Luise Herrmann bei GeoGebra)
4.2 Grundlagen der Vektorrechnung
- Der Vektorbegriff
In der Physik verwenden wir skalare Größen (Skalare), die durch die Angabe einer Maßzahl und einer Maßeinheit vollständig bestimmt sind (z.B. Masse , Zeit , Temperatur , Energie , ...).
Es gibt aber auch gerichtete Größen (Vektoren), die noch dazu auch die Angabe einer Richtung benötigen (z.B. Kraft , Geschwindigkeit , Impuls , Beschleunigung , ...).
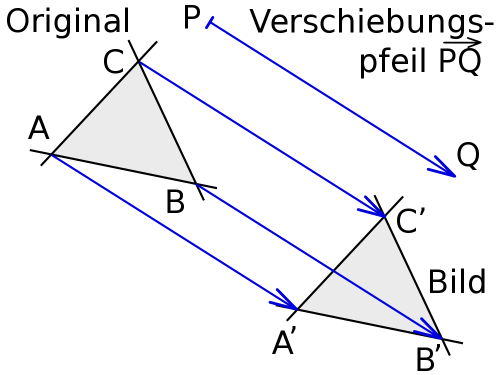
Wir betrachten eine Verschiebung:
Für den Verschiebungspfeil gilt:
Definition:
Die unendliche Menge aller Pfeile einer Verschiebung heißt Vektor. Ein einzelner Verschiebungspfeil daraus heißt Repräsentant des Vektors.
Ein Vektor wird bestimmt durch seine Richtung und seinen Betrag (entspricht der Länge des Vektorpfeils).
- Vektoren im Koordinatensystem
Sei mit und mit und mit .
Koordinatendarstellung eines Vektors (2-dimensional):
Betrag
Betrag
Betrag
(Prinzip:"Spitze minus Fuß", die Koordinaten des Punktes an der Spitze werden zeilenweise von den Koordinaten des Fußpunktes subtrahiert.)
Allgemein:
| Betrag |
Im 3-dimensionalen Fall ist die Koordinatendarstellung eines Vektors ein 3-Tupel:
| Betrag |
Beispiel: Vektor bestimmt durch die Punkte und
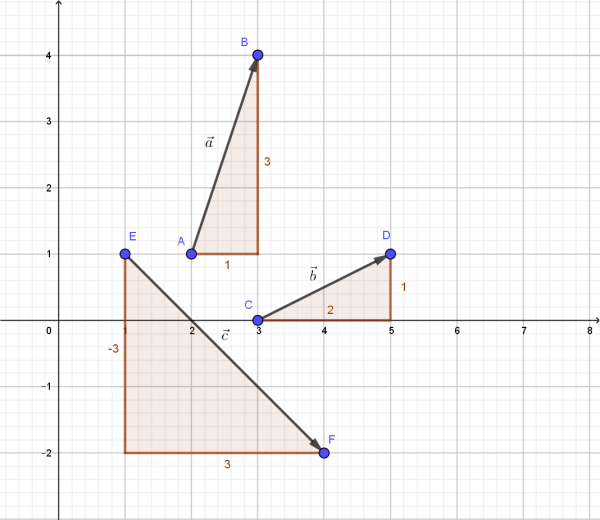
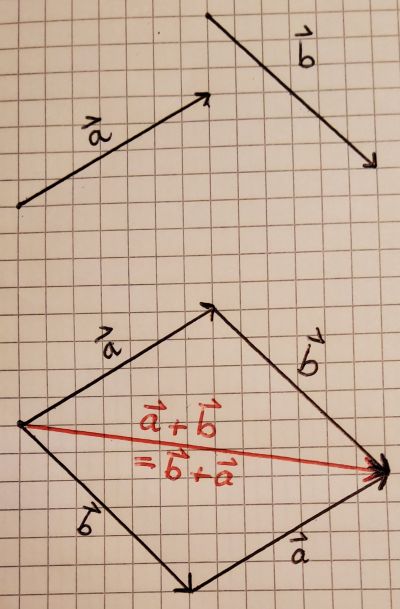
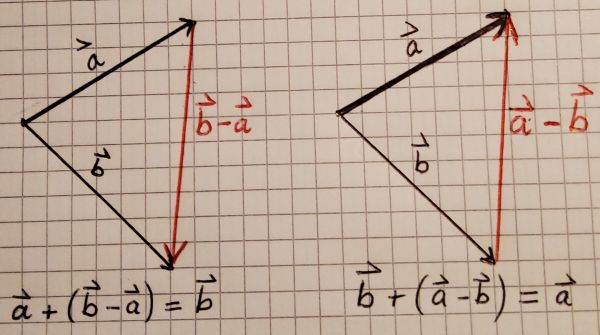
- Addition von Vektoren
Die Verkettung zweier Verschiebungen mit den Vektoren und ist wieder eine Verschiebung, deren Vektor der Summenvektor ist:
Die Vektoraddition ist kommutativ, das heißt .
Sie ist ebenfalls assoziativ: .
Koordinatendarstellung:
(Siehe auch Vektoraddition von Thorsten Glaser bei GeoGebra)
- Differenzvektor
Koordinatendarstellung:
(Siehe auch Subtraktion 3D von Werth bei GeoGebra)
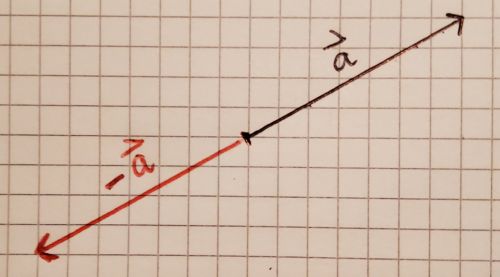
- Gegenvektor
Die Verschiebung mit den Vektoren wird durch die Verschiebung mit dem Gegenvektor rückgängig gemacht.
Koordinatendarstellung:
Die Subtraktion zweier Vektoren kann auch als Addition des Gegenvektors interpretiert werden: .
- Nullvektor
Die identische Abbildung (keine Verschiebung) hat den Verschiebungsvektor .
Der Nullvektor hat die Länge null, seine Richtung ist unbestimmt.
Koordinatendarstellung:
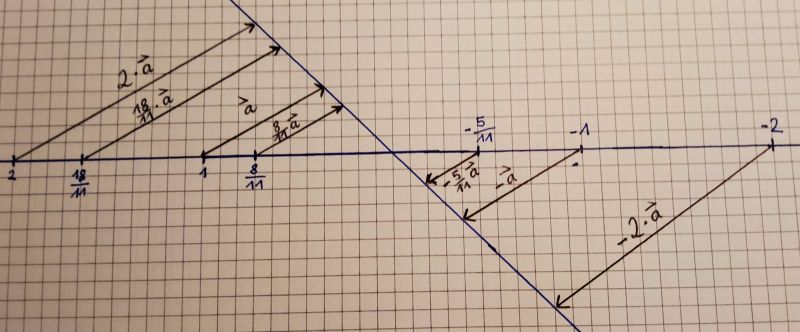
- Multiplikation eines Vektors mit einer Zahl, parallele Vektoren
Koordinatendarstellung:
(Siehe auch Multiplikation eines Vektors mit einem Skalar von lauragroessinger bei GeoGebra)
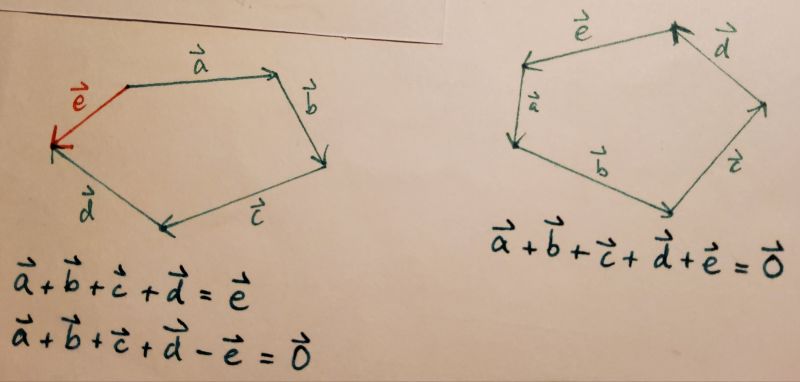
- Vektorketten
Eine mehrgliedrige Summe von Vektoren mit dem Summenvektor heißt geschlossene Vektorkette. Bei Aufgaben bevorzugt man oft solche geschlossenen Vektorketten.
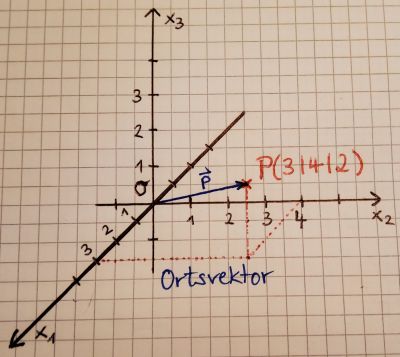
- Ortsvektoren
Zu jedem Punkt im Koordinatensystem gibt es einen Pfeil, der im Ursprung beginnt und in endet. Dieser Pfeil legt eindeutig einen Vektor fest, den man auch Ortsvektor des Punktes nennt (Schreibweise: ).
Koordinatendarstellung:
| Ortsvektor |
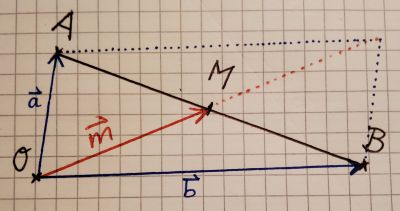
- Mittelpunkt einer Strecke
Gegeben sei eine Strecke zwischen den Punkten und mit den Ortsvektoren und .
Dann gilt:
| Ortsvektor des Mittelpunktes |
4.3 Betrag von Vektoren, Länge von Strecken
Die Länge eines Vektors heißt auch Betrag von :
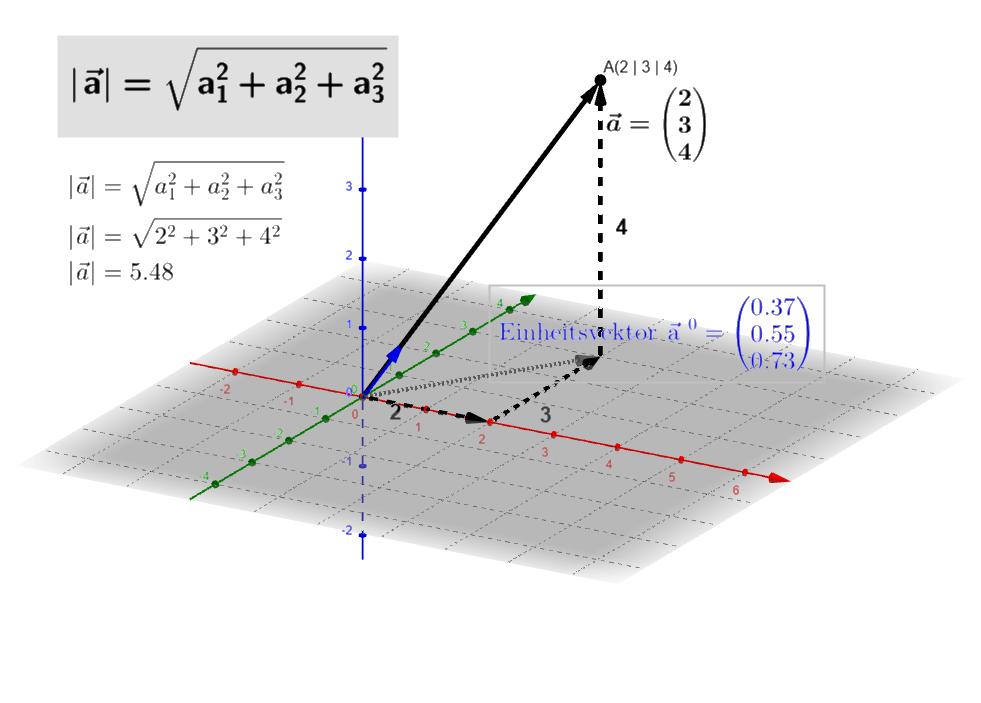 (Siehe auch Betrag eines Vektors 3D von JSmh bei geogebra.org)
(Siehe auch Betrag eines Vektors 3D von JSmh bei geogebra.org)
Die Länge einer Strecke ist: .
Vektoren der Länge 1 heißen Einheitsvektoren, zum Beispiel oder .
Den Einheitsvektor in die Richtung eines bestimmten vorgegebenen Vektors bezeichnet man mit .
Beispiele: In Richtung von ist der Einheitsvektor und in Richtung von ist der Einheitsvektor .
4.4 Skalarprodukt von Vektoren, Winkelberechnungen
Die Zahl
heißt Skalarprodukt der Vektoren und .
(Zur Herleitung siehe Skalarprodukt Herleitung und Anwendung by Lernen & Wissen bei YouTube.com)
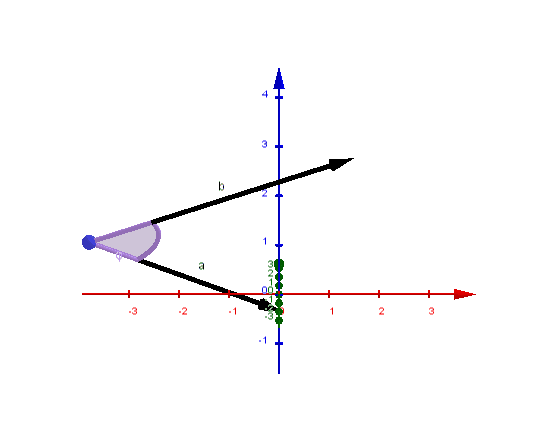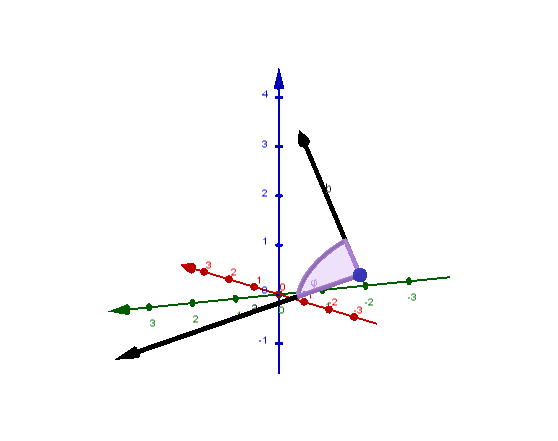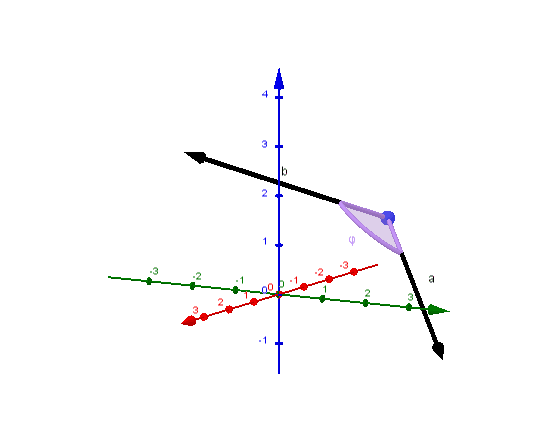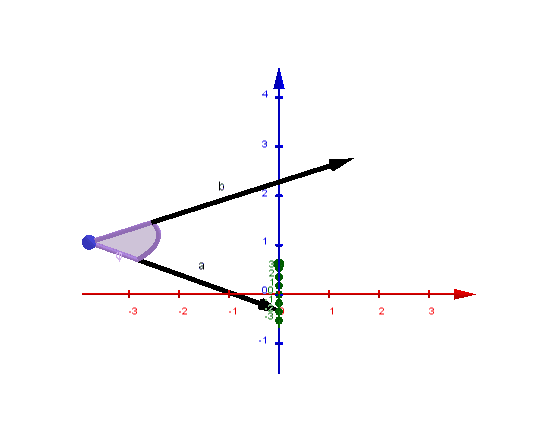
Es gilt:
wobei der Zwischenwinkel der Vektoren und ist.
Also gilt für den Zwischenwinkel zweier beliebiger Vektoren und :
Mit dem Skalarprodukt kann man Winkel zwischen Vektoren berechnen und insbesondere überprüfen, ob zwei Vektoren orthogonal (senkrecht) zueinander sind:
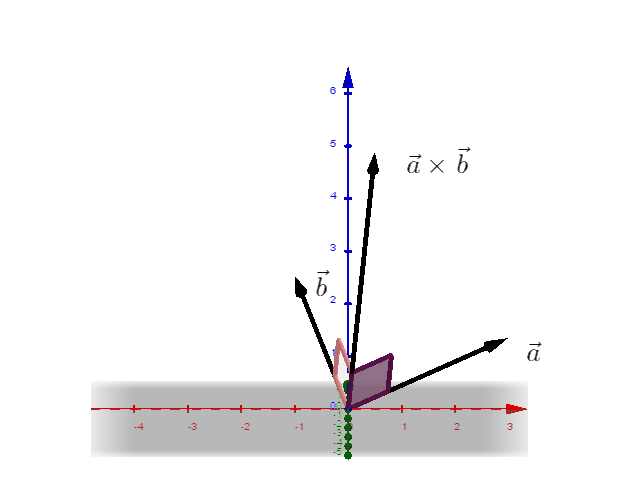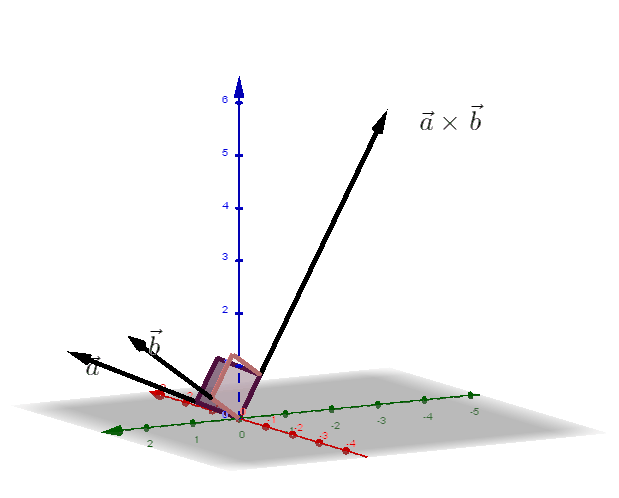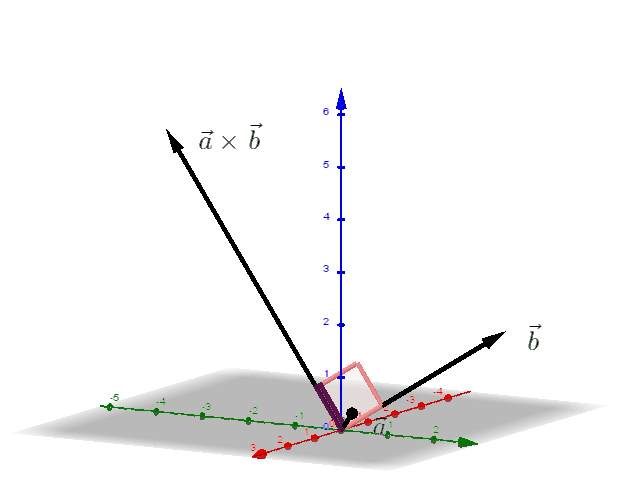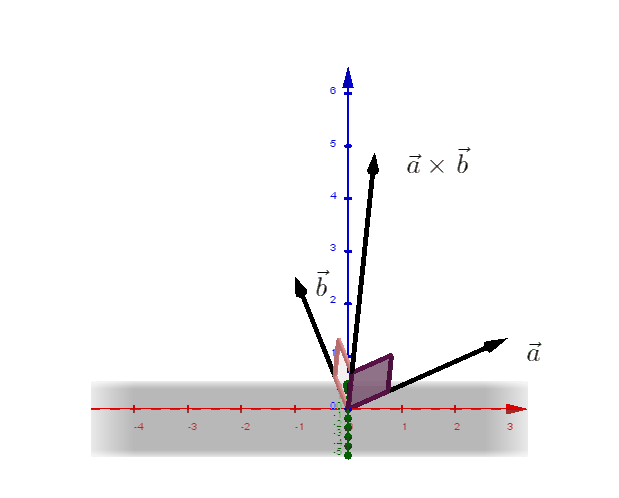
4.5 Das Vektorprodukt
Der Vektor
heißt Vektorprodukt (Kreuzprodukt) der Vektoren und .
ist orthogonal zu und zu .
- Anwendungen:
(1) Es gilt:
wobei der Zwischenwinkel der Vektoren und ist.
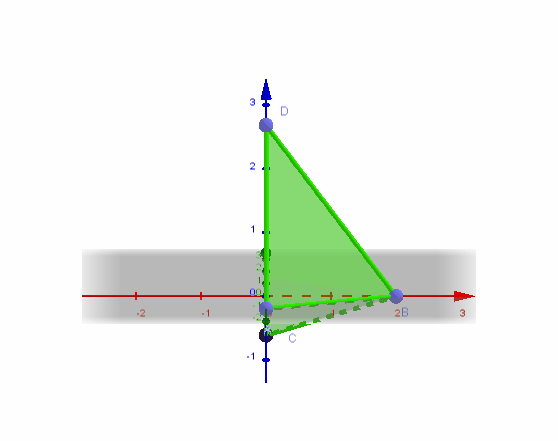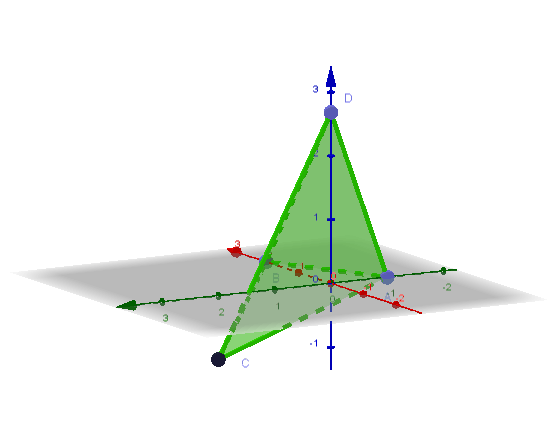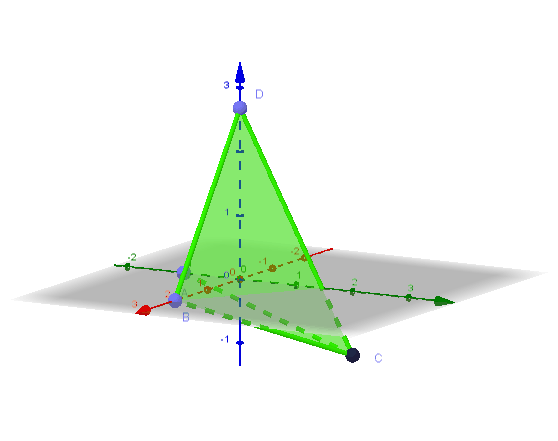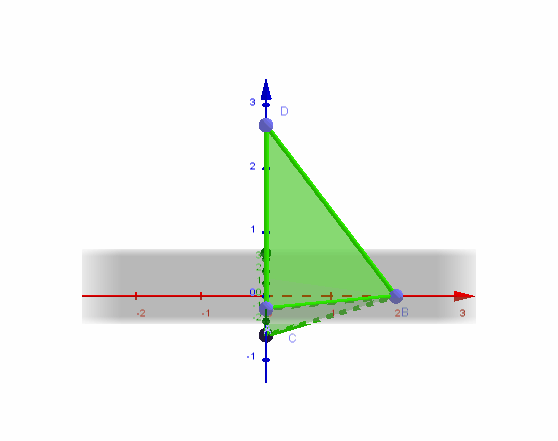
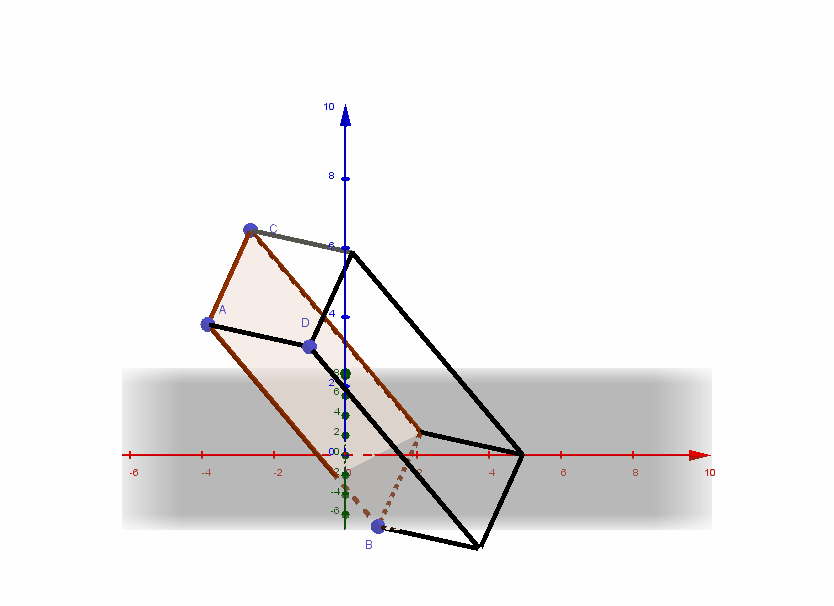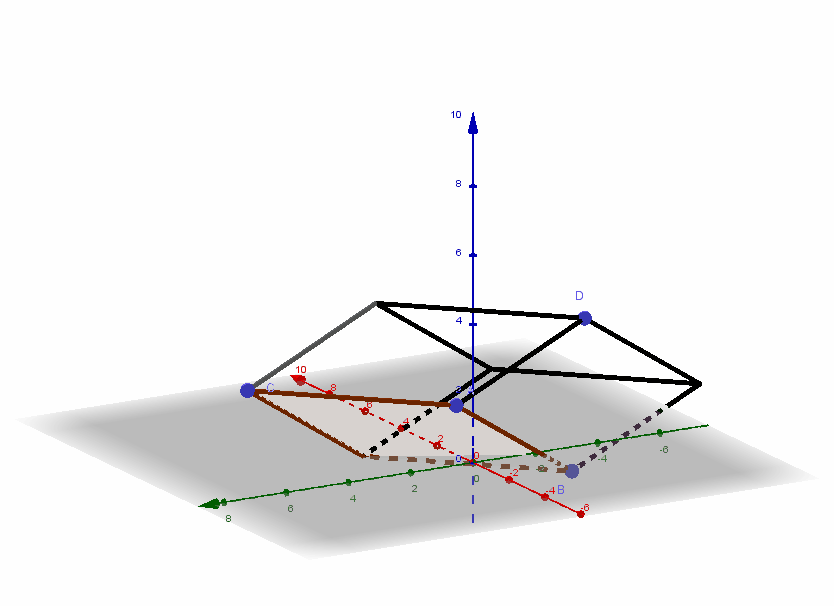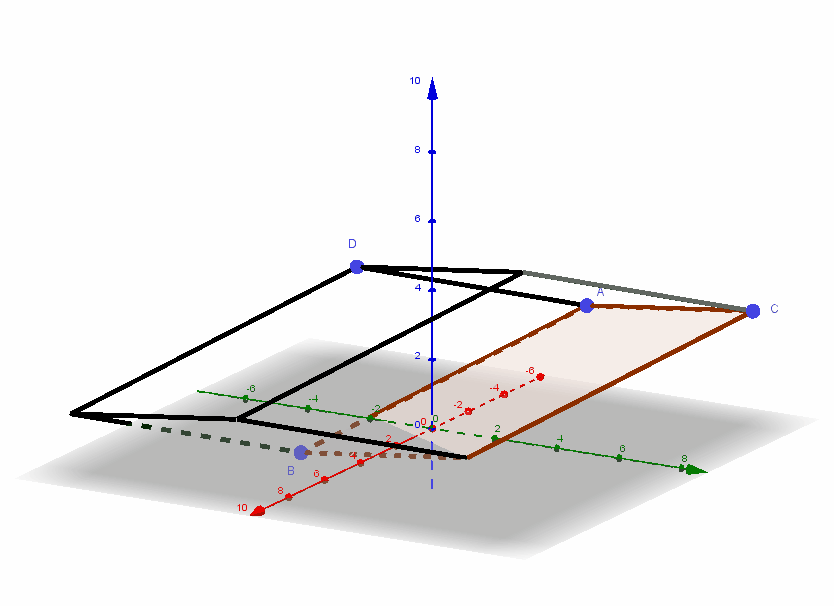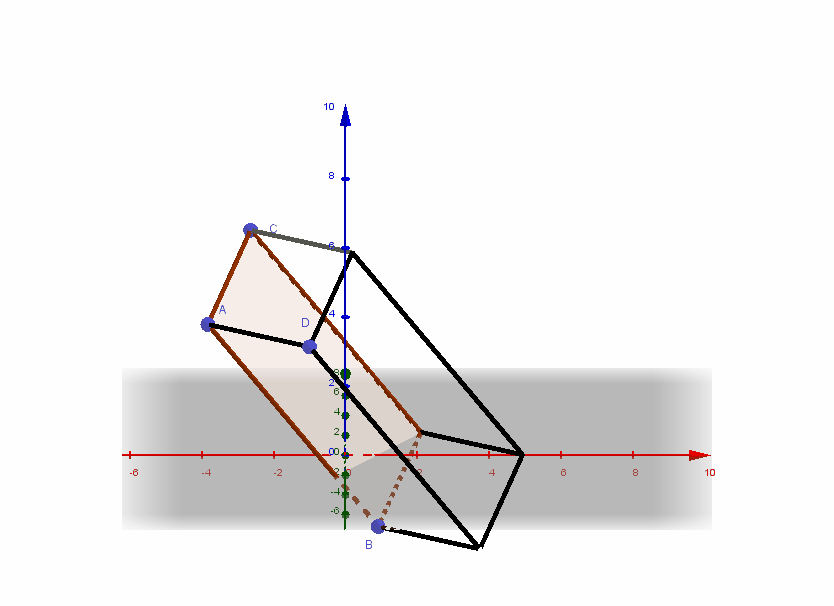
(2) Flächeninhalt des Dreiecks :
(3) Flächeninhalt des von und aufgespannten Parallelogramms :
(4) Volumen der von und aufgespannten Pyramide :
(5) Volumen des von und aufgespannten Parallelspats :
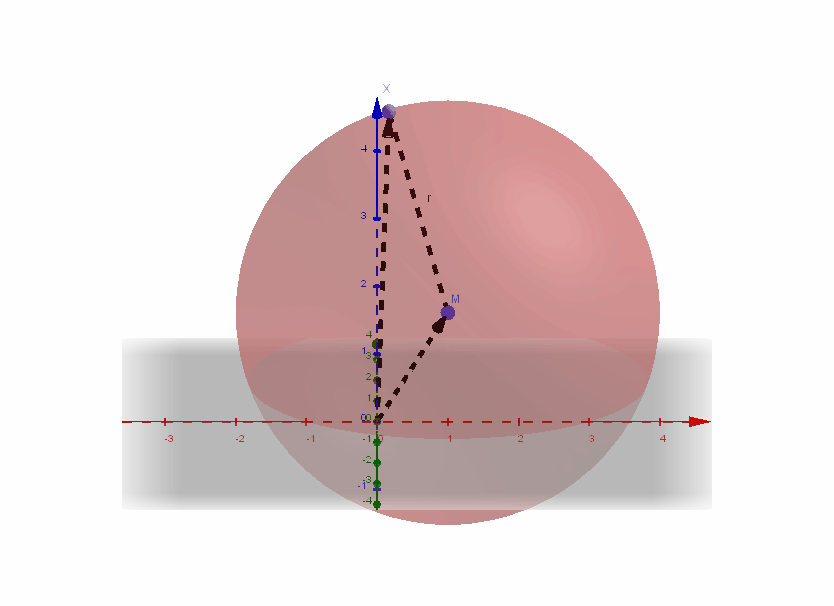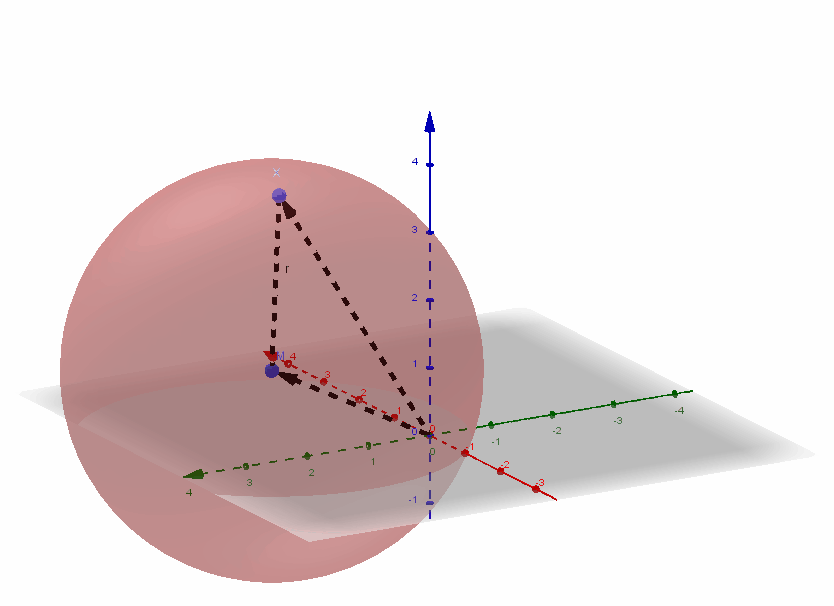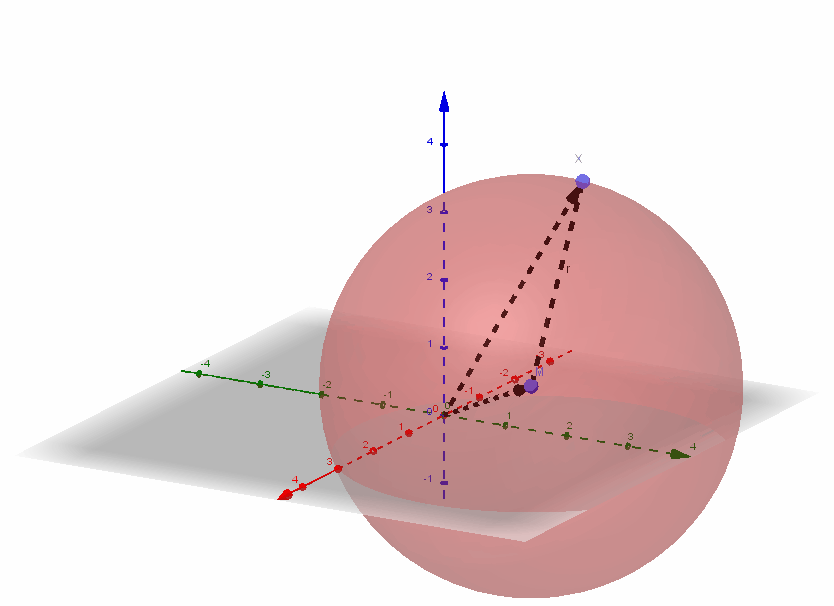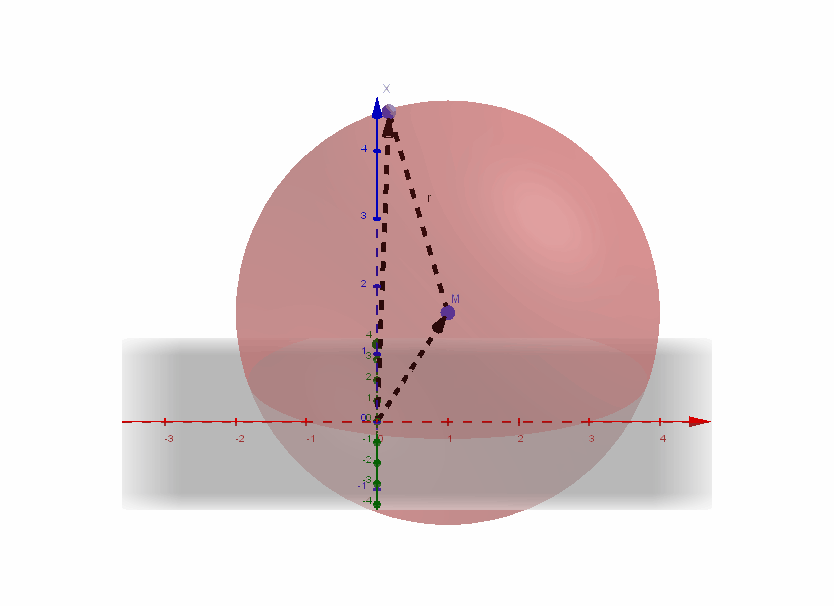
4.6 Kugeln im dreidimensionalen Koordinatensystem
Eine Kugel ist die Menge aller Punkte im Raum, die von einem festen Punkt den gleichen Abstand haben.
Eine Kugel mit Mittelpunkt und dem Radius wird beschrieben durch die Kugelgleichung:
(Achtung Skalarprodukt!)
(Siehe auch Kugel von Christian Barthel bei GeoGebra)
Wann liegt ein Punkt auf einer Kugel?
Ein Punkt liegt genau dann auf einer Kugel, wenn beim Einsetzen der Koordinaten des Punktes in die Kugelgleichung (für ) eine wahre Aussage entsteht, also .
Ist , so liegt außerhalb der Kugel, ist , so liegt innerhalb der Kugel.
- Beispiel:
ist die Kugelgleichung der Kugel mit dem Mittelpunkt mit dem Radius .
Der Punkt liegt auf der Kugel, da .
Der Punkt liegt innerhalb der Kugel, da .
Der Punkt liegt außerhalb der Kugel, da .
5. Differentialrechnung: Weitere Ableitungsregeln
5.1 Die Ableitung der Sinus- und Kosinusfunktionen
(Siehe zur Wiederholung zuerst Winkelfunktion von Kurt Söser bei GeoGebra)
Die Ableitung vom Sinus ist der Kosinus (Mathe-Song) vom DorFuchs bei youtube.com
- Aufgabenbeispiel:
Bestimmen Sie die Gleichungen der Tangente und der Normalen an den Graphen von im Punkt
Lösung:
Ansatz Tangente:
Also hier: Es ergibt sich:
Die gesuchte Tangentengleichung lautet:
Ansatz Normale: (für die Steigungen und zweier aufeinander senkrecht stehender Geraden gilt: !)
Also hier: Es ergibt sich:
Die gesuchte Normalengleichung lautet:
(zum Thema Normale siehe auch: Normale | Erklärung, Beispiel und Tipps by einfach mathe!)
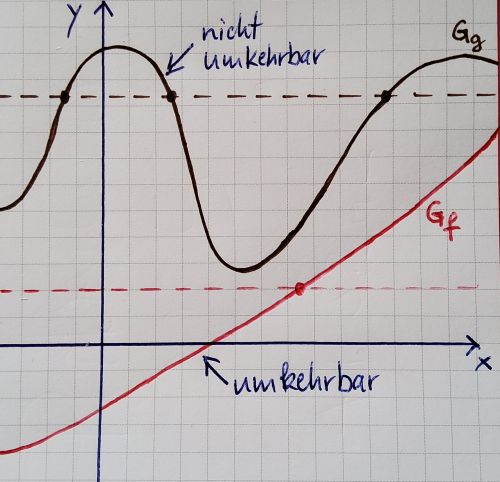
5.2 Umkehrfunktion / Umkehrbarkeit von Funktionen
(Siehe auch Buch S. 130 und S. 131)
(Siehe zur Wiederholung zuerst das Video Was ist eine Funktion? von Videolernen bei YouTube.com)
- Frage: Was ist eine Funktion? Antwort: Eine Funktion ist eine eindeutige Zuordnung.
Wir kennen aus der Mathematik bereits Umkehroperationen (Addition <--> Subtraktion, Multiplikation <--> Division, ...) und aus dem Alltag zueinander umgekehrte Vorgänge (Einpacken <--> Auspacken, Vorwärts <--> Rückwärts, ...).
Ebenso kann man bei einer Funktion die umgekehrte Zuordnung betrachten.
Allerdings führt das nicht immer zu einer eindeutigen Umkehrfunktion, da die umgekehrte Zuordnung nicht immer eindeutig ist!
Beispiel: Jedem der 30 Schüler einer Klasse wird bei einer Schulaufgabe eindeutig eine Note zugeordnet. Während diese Zuordnung eine Funktion ist, ist die umgekehrte Zuordnung keine Funktion, da nicht jeder Note eindeutig ein Schüler zugeordnet werden kann.
Deswegen:
Definition Umkehrbarkeit:
| Eine Funktion heißt umkehrbar, wenn auch die umgekehrte Zuordnung wieder eindeutig ist. |
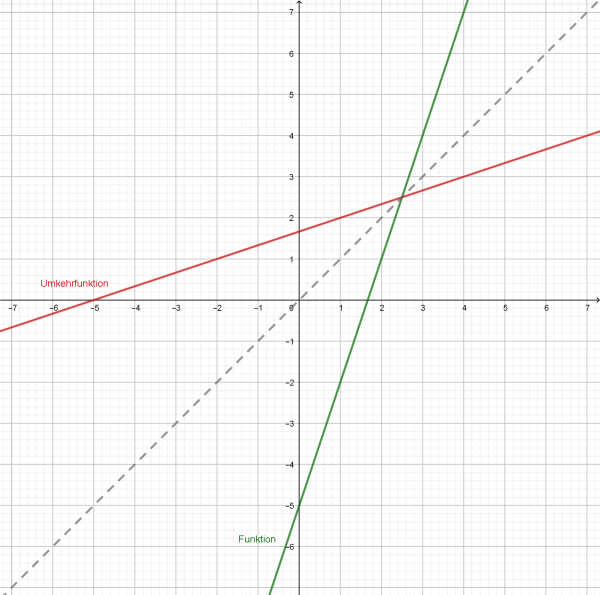
- Betrachte eine Funktion mit der Zuordnungsvorschrift .
Dann ist die Umkehrfunktion mit der Zuordnungsvorschrift .
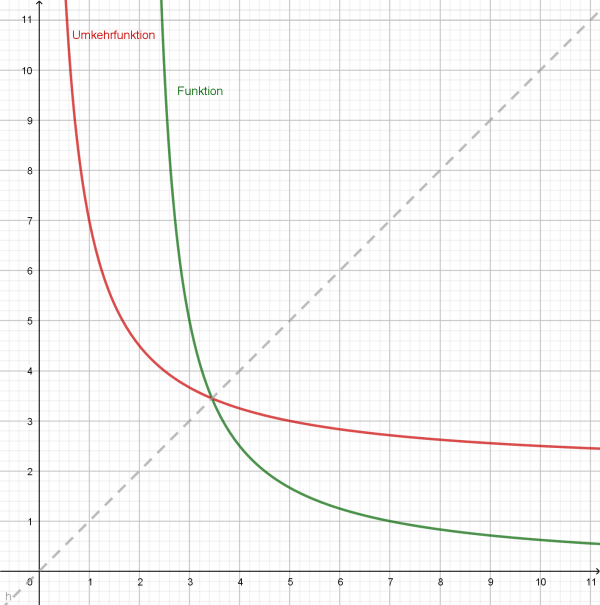
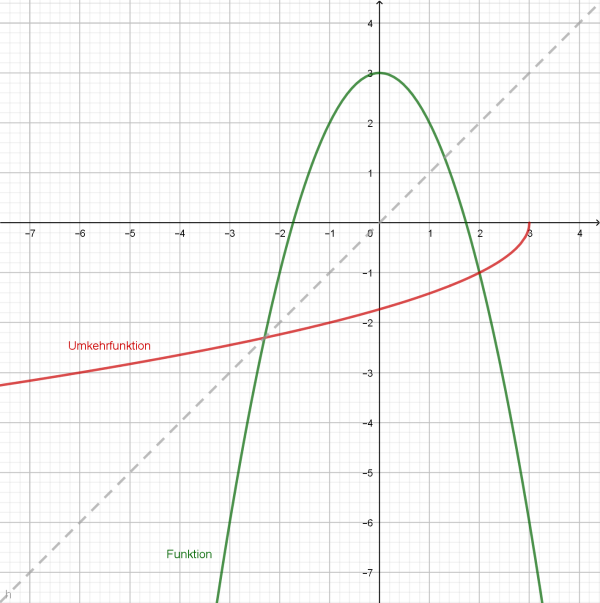
- Graphisch bekommt man die Umkehrfunktion, indem man den Graphen der Funktion an der Winkelhalbierenden des I. und III. Quadranten im Koordinatensystem spiegelt.
(Siehe ACHTAU - ACHsen TAUschen: Graph der Umkehrfunktion von Jürgen Roth bei GeoGebra)
- Rechnerisch bestimmt man die Funktionsgleichung der Umkehrfunktion folgendermaßen:
(1) Auflösen der Funktionsgleichung nach ;
(2) Vertauschen von und ;
(3) Funktionsgleichung der Umkehrfunktion damit aufstellen; Es gilt:
Kriterium für die Umkehrbarkeit einer Funktion:
| Eine streng monotone Funktion ist umkehrbar. |
Falls es bei einer Funktion zu einem y-Wert mehrere zugehörige x-Werte gibt, so ist die Funktion also nicht umkehrbar!
- Aufgabenbeispiel 1:
Zeigen Sie, dass mit umkehrbar ist und bestimmen Sie die Umkehrfunktion!
Lösung:
für alle ;
Also ist streng monoton fallend und somit umkehrbar.
Bestimmung des Funktionsterms der Umkehrfunktion:
;
Nach Vertauschen von und ergibt sich: , also ;
Betrachtung der Definitions- und Wertemengen: , für die Umkehrfunktion:
- Aufgabenbeispiel 2:
Zeigen Sie, dass mit umkehrbar ist und bestimmen Sie die Umkehrfunktion!
Lösung:
für alle und für ;
Also ist streng monoton steigend und somit umkehrbar.
;
Bestimmung des Funktionsterms der Umkehrfunktion:
;
Nach Vertauschen von und ergibt sich: , also ;
Das Minuszeichen vor der Wurzel wird genommen, da die Werte der Umkehrfunktion negativ oder null sind: .
;
5.3 Ableitung verketteter Funktionen / die Kettenregel
(Siehe auch Buch S. 136 und S. 137)
Manche Funktionsterme sind durch "Verschachtelung" verschiedener Funktionen entstanden. Man nennt solche Fuktionen verkettete Funktionen, da sie aus einfacheren Funktionen durch Verkettung entstehen.
- Beispiele: , oder .
Kettenregel:
| Sei eine Verkettung zweier differenzierbarer Funktionen und . Dann ist auch differenzierbar und es gilt: |
Das Bilden des Faktors nennt man auch Nachdifferenzieren.
Tipp: Bei Anwendung der Kettenregel sollte man sich die Terme "verschachtelt" denken und beim Ableiten wie beim Auspacken vorgehen: Von außen nach innen schrittweise. Und bei jedem Schritt muss man einmal nachdifferenzieren.
- In unseren Beispielen:
- Weitere Beispiele:
(Nur Quotientenregel)
(In der Quotientenregel muss man hier nachdifferenzieren!)
(Zweimal nachdifferenzieren!)
(Achtung! Es wird nach t differenziert!)
5.5 Ableitung von Potenzfunktionen mit rationalen Exponenten
(Siehe auch Buch S. 139 und S. 140)
Wir wollen nun auch Potenzfunktionen mit Brüchen im Exponenten ableiten. Dazu gilt folgende Regel:
| Sei . Dann ist: |
- Beispiele:
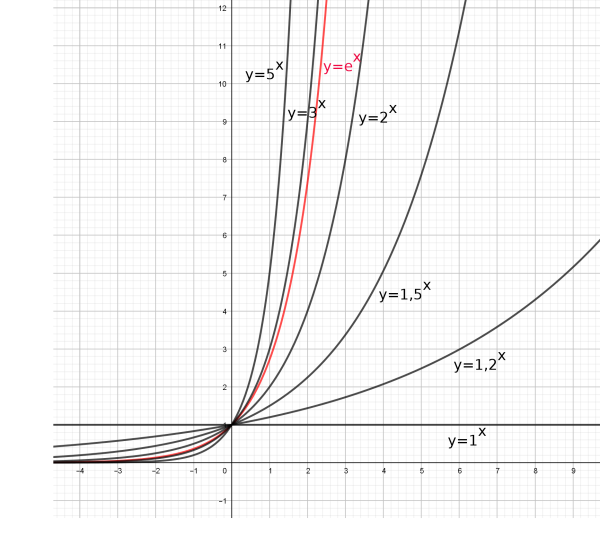
6. Natürliche Exponential- und Logarithmusfunktionen
Zum Einstieg arbeite durch: Thema Exponentialfunktionen bei BR alpha Lernen
6.1 Die natürliche Exponentialfunktion
Untersucht man die Ableitungen der Exponentialfunktionen näher, so fällt auf, dass es eine darunter geben muss, die "sich selbst als Ableitung" hat:
| Die natürliche Exponentialfunktion hat die Ableitung und als eine mögliche Stammfunktion . |
Die Zahl heißt Eulersche Zahl und ist wie oder eine irrationale Zahl. Es gilt .
- Eigenschaften der e-Funktion
Definitionsmenge: , Wertemenge:
Der Graph der e-Funktion ist streng monoton steigend.
| Für geht |
Funktionalgleichungen (Potenzgesetze):
Da die ln-Funktion die Umkehrfunktion zur e-Funktion ist, gilt:
Kurvendiskussion mit e-Funktion von mathegym bei Youtube.com
Video Die e-Funktion und ihre Ableitung von Flip the Classroom bei youtube.com
Grundwissen zur natürlichen Exponentialfunktion bei strobl-f.de
Übungsaufgaben zur e-Funktion bei strobl-f.de
6.2 Die natürliche Logarithmusfunktion
Zur Wiederholung siehe folgende drei Lernvideos:
Logarithmenregeln bei unterricht.de
Logarithmus im Exponenten bei unterricht.de
Definition:
| Die Logarithmusfunktion zur Basis heißt natürliche Logarithmusfunktion.
mit ; |
Sie ist die Umkehrfunktion zur natürlichen Exponentialfunktion.
- Eigenschaften der ln-Funktion
Definitionsmenge: , Wertemenge:
Der Graph der ln-Funktion ist streng monoton steigend.
| Für geht | Für geht |
Funktionalgleichungen (Logarithmengesetze):
Da die ln-Funktion die Umkehrfunktion zur e-Funktion ist, gilt:
Ableitung der ln-Funktion:
Stammfunktion der ln-Funktion:
Grundwissen zur natürlichen Logarithmusfunktion bei strobl-f.de
Übungsaufgaben zur ln-Funktion bei strobl-f.de
Natürliche Logarithmusfunktion - Log Naturalis von StrandMathe bei YouTube.com
6.3 Wichtige Grenzwerte im Zusammenhang mit natürlicher Exponential- und Logarithmusfunktion
Die natürliche Exponentialfunktion wächst für "schneller" als jede Potenz mit :
Umgekehrt wächst die natürliche Logarithmusfunktion für "langsamer" als jede Potenz mit :
Außerdem kann man zeigen, dass gilt:
7. STOCHASTIK: Wahrscheinlichkeit und Unabhängigkeit
Zum Einstieg wiederhole:
Grundwissen 8. Klasse zu Wahrscheinlichkeiten, Laplace-Experimente bei strobl-f.de
Grundwissen 9. Klasse zu mehrstufigen Zufallsexperimenten bei strobl-f.de
Grundwissen 10. Klasse zur bedingten Wahrscheinlichkeit bei strobl-f.de
In der Stochastik wird anhand einer realen Situation ein mathematisches Modell entwickelt, mit dem man Berechnungen durchführen kann und dessen Ergebnis dann in der Realität eine Bedeutung im Hinblick auf die reale Situation hat.
(Siehe dazu Beispiel "Pyramide liegt auf einer Seitenfläche" im Modellierungskreislauf im Buch S. 175)
7.1 Axiomatische Definition von Wahrscheinlichkeit
Ausgehend von wenigen, grundlegenden Aussagen bzw. Festlegungen ("Axoime"), kann man die Wahrscheinlichkeitsrechnung lückenlos formulieren und komplett beweisen.
Der russische Mathematiker Kolmogorow hat so ein Axiomensystem zur Definition des Wahrscheinlichkeitsbegriffs aufgestellt:
| Sei eine (Ergebnis-) Menge und eine Teilmenge (Ereignis) davon.
Dann heißt eine Funktion Wahrscheinlichkeitsverteilung, wenn sie folgende Axoime erfüllt: (I) (Nicht-Negativität) (II) (Normiertheit) (III) Für gilt: (Additivität) |
heißt Wahrscheinlichkeit vom Ereignis .
wird auch Wahrscheinlichkeitsraum genannt.
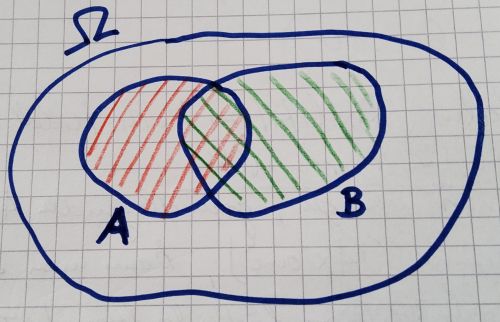
7.2 Der Ereignisraum
Siehe Der Ereignisraum - eine Übersicht zur Ereignis-Algebra
7.3 Der Additionssatz für Wahrscheinlichkeiten von Ereignissen
Zum Einstieg ein Lernvideo: Additionssatz und Vierfeldertafel - Mathe - SchullV bei YouTube.com
Für beliebige Ereignisse gilt der Additionssatz:
Oder umgestellt:
Für zwei unvereinbare (disjunkte) Ereignisse (für die gilt), ist also: .
7.4 Stochastische Unabhängigkeit von Ereignissen
Hat (1) das Eintreten von Ereignis keinen Einfluss auf das Eintreten von Ereignis
und umgekehrt
das (2) Eintreten von Ereignis keinen Einfluss auf das Eintreten von Ereignis ,
so sind beide Ereignisse (stochastisch) unabhängig.
Oder mathematisch kurz formuliert:
Ist (1)
und (2) ,
so sind beide Ereignisse (stochastisch) unabhängig.
Aus (1) und (2) ergibt sich folgende
Definition stochastische Unabhängigkeit:
| Zwei Ereignisse heißen (stochatisch) unabhängig, wenn
gilt. Andernfalls heißen die beiden Ereignisse (stochastisch) abhängig voneinander. |
Zum besseren Verständnis ein Lernvideo: Ereignisse auf stochastische Abhängigkeit prüfen von Mathehoch13 bei YouTube.com
8. Anwendungen der Differentialrechnung
Zur Übung empfehlenswert: Abituraufgaben Bayern 2020, 2019 und 2018, jeweils Teil B Analysis (soweit mit dem Stoff der Q11 lösbar).
Diese Aufgaben mit Lösung finden sich zum Beispiel bei abiturloesung.de.
Mathematik GWM5 GWM6 GWM7 GWM8 GWM9 SchulheftM5 SchulheftM6 SchulheftM10 SchulheftM12



















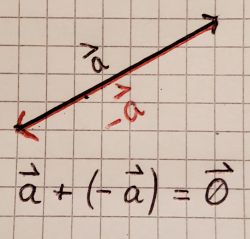








































![{\displaystyle \mathbb {W} _{g^{-1}}=]-\infty ;0]=\mathbb {D} _{g};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8126e0cd67c5e4991cb7758d0523b86110bd3fc6)




![{\displaystyle f'(x)=u'[v(x)]\cdot v'(x)\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1536a1f075cd5934c31cd134a22866b75611c594)
![{\displaystyle f'(x)=[2\cdot (3x-7)]\cdot 3=18x-42}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23b770e794189e4af6cc621a4a4edc83ed512318)

![{\displaystyle f(x)=sin[(ax)^{2}]\Rightarrow f'(x)=cos[(ax)^{2}]\cdot 2ax\cdot a=2a^{2}x\cdot cos[(ax)^{2}];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a20f95f9389c9bf18a5f44e0c0efc8723d3b2cf1)
![{\displaystyle f(x)=a\cdot x^{\frac {p}{q}}=a\cdot {\sqrt[{q}]{x^{p}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c0800b3bc33a2c49d328472a2834b140d661bf1)

![{\displaystyle h(x)=k\cdot {\sqrt[{5}]{x^{p-3}}}\Rightarrow h'(x)={\frac {k\cdot (p-3)}{5}}\cdot x^{\frac {p-8}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47a93213853610217bb647083b315d7e36dbf1b9)