GWM8
Inhaltsverzeichnis
- 1 Grundwissen Mathematik 8. Klasse
- 1.1 GWM 8.1 Proportionalitäten
- 1.2 GWM 8.2 Funktionen
- 1.3 GWM 8.3 Gleichungen mit zwei Variablen und Gleichungssysteme
- 1.4 GWM 8.4 Bruchterme und Bruchgleichungen
- 1.5 GWM 8.5 Die Zentrische Streckung
- 1.6 GWM 8.6 Ähnlichkeit
- 1.7 GWM 8.7 Kreise
- 1.8 GWM 8.8 Potenzgesetze für ganzzahlige Exponenten
- 1.9 GWM 8.9 Ergebnisraum
- 1.10 GWM 8.10 Das Ereignis
- 1.11 GWM 8.11 Laplace-Wahrscheinlichkeit
Grundwissen Mathematik 8. Klasse
Diese Fassung muss noch überarbeitet werden!!!
GWM 8.1 Proportionalitäten
| Direkte Proportionalität | Indirekte Proportionalität | |
| Dem n-fachen der einen Größe wird das n-fache der anderen Größe zugeordnet. | Dem n-fachen der einen Größe wird der n-te Teil der anderen Größe zugeordnet. | |
| Zuordnungs-vorschrift |
heißt Proportionalitätsfaktor |
|
| Erkennungs-zeichen | Quotientengleichheit
|
Produktgleichheit
|
| Graph | Ursprungsgerade
Bsp.: |
Hyperbel
Bsp.: |
GWM 8.2 Funktionen
Der Zusammenhang zwischen zwei Größen kann oft durch eine Zuordnung beschrieben werden.
Eine Zuordnung , die jedem Element aus der einen Menge (=Definitionsmenge) genau ein Element einer anderen Menge zuordnet, heißt Funktion.
Unterscheide folgende Begriffe:
Funktionsvorschrift: Beispiel:
Funktionsterm: Beispiel:
Funktionsgleichung: Beispiel:
Definitionsmenge: Menge aller zulässigen Werte für aus einer Grundmenge
Wertemenge: Menge aller (beim Einsetzen von ) auftretenden Funktionswerte
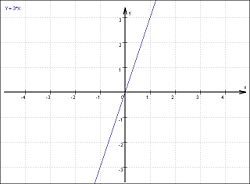
Die lineare Funktion:
Der Graph einer linearen Funktion ist eine Gerade. Sie schneidet die y-Achse im Punkt (0 / t) Man nennt t deshalb y-Achsenabschnitt. Für m > 0 steigt die Gerade, für m < 0 fällt die Gerade.
Zeichnen der Gerade mit dem Steigungsdreieck: Ausgehend vom Punkt (0/t) gehe 1 LE nach rechts und dann um m nach oben, falls m >0 oder um m nach unten, falls m < 0. Hier liegt der zweite Punkt.
Aufstellen der Gerade durch zwei Punkte: Bsp. Gerade durch A(2 / 4) und B(5 / 0) Berechnung von m: (Gerade fällt) Berechnung von t: allgemeine Form y = mx + t Die Koordinaten der Punkte, die auf der Geraden liegen, erfüllen die Funktionsgleichung Koordinaten von A (oder von B) einsetzen nach t auflösen Ergebnis: Die Punkte A und B bestimmen die Gerade
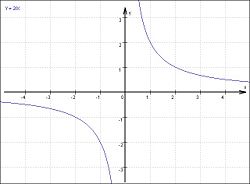
Die gebrochenrationale Funktion: z. B.
Der Funktionsterm einer gebrochenrationalen Funktion ist ein Bruchterm. Die Variable x kommt auch im Nennerterm vor.
Definitionsmenge: Alle Zahlen, für die der Nenner Null wird, können nicht zur Definitionsmenge gehören. Definitionslücken.
Der Graph hat an den Definitionslücken dann jeweils eine senkrechte Asymptote. (Eine Gerade, der sich die Funktionswerte einer Funktion beliebig genau nähern, nennt man Asymptote.) Eine gebrochenrationale Funktion hat oft auch eine waagrechte Asymptote.
D = Q\{-3}
Definitionslücke bei x = -3
Senkrechte Asymptote bei x = -3
Waagrechte Asymptote ist eine Parallele zur x-Achse, da x in Zähler und Nenner in der gleichen Potenz auftritt. (hier: Asymptote: y = 2) Waagrechte Asymptote ist die die x-Achse, wenn x im Nenner in einer höheren Potenz als im Nenner auftritt.
GWM 8.3 Gleichungen mit zwei Variablen und Gleichungssysteme
Gleichungen der Form 3x – 4y = 8 heißen lineare Gleichungen mit zwei Variablen. Die graphische Darstellung der Lösungsmenge ist eine Gerade Jede Gleichung hat unendlich viele Lösungen, jede Lösung besteht aus einem Zahlenpaar.
Bsp. 3x – 4y = 8 3x – 8 = 4y y = 0,75x – 2 (lineare Funktion, d.h. Graph ist eine Gerade) Lösungen sind z. B.: (1 / -1,25); (2/-0,5); usw.
Zwei lineare Gleichungen, die zwei Variablen enthalten, bilden ein Gleichungssystem. Da jede der beiden Gleichungen eine Gerade darstellt, wird bei der Lösung eines linearen Gleichungssystems der Schnittpunkt der beiden Geraden berechnet. Es gibt deshalb drei Möglichkeiten: Geraden sind parallel: kein Schnittpunkt L = {} Geraden schneiden sich: L = {(xs ; ys)} S Schnittpunkt Geraden sind identisch: L hat unendlich viele Elemente
Rechenverfahren zur Lösung von Gleichungssystemen:
Einsetzverfahren: Eine Gleichung wird nach einer Variablen aufgelöst. Der gefundene Term wird dann in die andere Gleichung eingesetzt. Diese Gleichung hat dann nur noch eine Variable und kann danach aufgelöst werden. Dann muss die andere Variable noch berechnet werden.
Gleichsetzverfahren: Beide Gleichungen werden nach der gleichen Variablen aufgelöst. Die gefundenen Terme werden gleichgesetzt und dann nach der verbliebenen Variablen aufgelöst. Danach kann die andere Variable berechnet werden.
Additionsverfahren: Die beiden Gleichungen werden so addiert, dass eine Variable wegfällt. Vorher muss meist eine Gleichung mit einer geeigneten Zahl multipliziert werden. Dann nach der verbliebenen Variablen auflösen, ...
Beispiel: I. 4x + 3y = 23 II. 2x – 3y = 7
Einsetzverfahren Gleichsetzverfahren Additionsverfahren I’:
In II: 2( ) -4,5y = 7 – 11,5 y = 1 in I’: x = 5
L = {(5 /1)} I’: 3y = 23 – 4x II’: 3y = -7 + 2x
I’ = II’: 3 – 4x = -7 + 2x 30 = 6x 5 = x in I’: 3y = 23 – 20 y = 1 L = {(5 /1)} I: 4x + 3y = 23 II: 2x – 3y = 7 I + II: 6x = 30 x = 5 In I: 20 + 3y = 23 y = 1
L = {(5 /1)}
GWM 8.4 Bruchterme und Bruchgleichungen
Terme mit Variablen im Nenner, heißen Bruchterme. Für das Rechnen mit Bruchtermen, sowie dem Kürzen und Erweitern, gelten die Regeln wie bei der Bruchrechung!!!
Z.B.: Bruchterme werden addiert (subtrahiert), indem man sie auf den Hauptnenner erweitert, die Zähler addiert (subtrahiert) und den Nenner beibehält. Zur Bestimmung des Hauptnenners werden zuerst alle Nenner faktorisiert.
Gleichung mit Brüchen, deren Nenner Variablen enthalten, heißen Bruchgleichungen.
Bruchgleichungen löst man, indem man 1. den Hauptnenner bestimmt, 2. daraus die Definitionsmenge bestimmt (Nenner Nie Null), 3. beide Seiten der Gleichung mit dem Hauptnenner multipliziert. 4. Nach dem Kürzen erhält man eine Gleichung ohne Nenner, die man löst. 5. Die Lösung muss in der Definitionsmenge enthalten sein.
GWM 8.5 Die Zentrische Streckung
Ein Parallelenpaar wird von einer Geradenkreuzung geschnitten.
Strahlensatz:
Wenn zwei Geraden g1 und g2 mit dem gemeinsamen Punkt Z von zwei parallelen Geraden (außerhalb von Z) geschnitten, so verhalten sich
1. je zwei Abschnitte auf g1 wie die entsprechenden Abschnitte auf g2,
2. die Abschnitte auf den Parallelen wie die von Z aus gemessenen entsprechenden Abschnitte auf g1 (oder g2).
Bemerkung: Es gilt der Kehrsatz zum 1. Teil des Strahlensatzes:
Werden zwei Geraden g1 und g2 mit dem gemeinsamen Punkt Z von zwei Geraden h1 und h2 (außerhalb von Z) so geschnitten, dass je zwei Abschnitte auf g1 sich wie die entsprechenden Abschnitte auf g2 verhalten und die gebildeten Dreiecke bei Z einen gemeinsamen Innenwinkel haben oder die Innenwinkel bei Z Scheitelwinkel sind, so sind die Geraden h1 und h2 parallel.
GWM 8.6 Ähnlichkeit
Eine Verkettung von zentrischen Streckungen und Kongruenzabbildungen heißt Ähnlichkeits-abbildung; je nachdem ob sie den Umlaufsinn beibehält oder ändert, heißt sie gleichsinnig oder gegensinnig. Lässt sich eine Figur F durch eine Ähnlichkeitsabbildung auf eine Figur G abbilden, so sagt man: F und G sind ähnlich. F G.
Ähnlichkeitssätze W:W-Satz: Zwei Dreiecke sind ähnlich, wenn sie in zwei Winkeln übereinstimmen. S:S:S-Satz: Zwei Dreiecke sind ähnlich, wenn sie im Verhältnis ihrer Seiten übereinstimmen. S:W:S-Satz: Zwei Dreiecke sind ähnlich, wenn sie im Verhältnis zweier Seiten und dem eingeschlossenen Winkel übereinstimmen. S:s:W-Satz: Zwei Dreiecke sind ähnlich, wenn sie im Verhältnis zweier Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen. Schreibweise: ABC ~ A’B’C’ Umkehrung: Sind zwei Dreiecke ähnlich, so stimmen sie in den Winkeln überein und die Verhältnisse entsprechender Seiten sind gleich.
GWM 8.7 Kreise
Ein Kreis mit dem Radius r besitzt den Umfang U = 2 r = d und den Flächeninhalt A = r2
GWM 8.8 Potenzgesetze für ganzzahlige Exponenten
Potenzen: , a Q, n N , a Q\{0} , n N Beachte: a1 = a; a0 = 1, a-1 = Potenzgesetze: an am = an + m (gleiche Basis) mit a, b Q\{0} und n, m Z an bn = (ab)n (gleicher Exponent) Gleitkommadarstellung: 120000 = 1,2 105, 0,00000036 = 3,6 10-7
GWM 8.9 Ergebnisraum
Ein Experiment, dessen Ausgang nicht vorhersagbar ist, heißt Zufallsexperiment. Den Ausgang eines Experiments nennt man Ergebnis. Alle möglichen Ergebnisse eines Zufallsexperiments ergeben den Ergebnisraum . Beispiele: Einmaliges Werfen eines Würfels: = {1; 2; 3; 4; 5; 6} Zweimaliges Werfen einer Münze: = {KK;KZ; ZK; ZZ}
GWM 8.10 Das Ereignis
Kein, ein oder mehrere Ergebnisse kann man zu einem Ereignis E zusammenfassen. Ereignis mit einem Element sind Elementarereignisse. Beispiele: E1: „Eine gerade Augenzahl wird gewürfelt“: E1 = {2;4;6} E2: „Eine 6 wird gewürfelt“: E2 ={6} (Elementarereignis) Das Gegenereignis tritt ein, wenn E nicht eintritt. Beispiele: = {1;3;6} = {1; 2; 3; 4; 5} Sonderfälle: Für das sicher Ereignis gilt: E = Für das unmögliche Ereignis gilt: E = { }
GWM 8.11 Laplace-Wahrscheinlichkeit
Zufallsexperimente, deren Elementarereignisse immer die gleiche Wahrscheinlichkeit besitzen, heißen Laplace-Experimente.
Für die Wahrscheinlichkeit eines Ereignisses gilt:
Beispiele: