GWM7
Inhaltsverzeichnis
- 1 Grundwissen Mathematik 7. Klasse
- 1.1 GWM 7.1 Achsensymmetrie
- 1.2 GWM 7.2 Konstruktionen
- 1.3 GWM 7.3 Punktsymmetrie
- 1.4 GWM 7.4 Vierecke
- 1.5 GWM 7.5 Winkel
- 1.6 GWM 7.6 Terme
- 1.7 GWM 7.7 Gleichungen
- 1.8 GWM 7.8 Daten, Diagramme
- 1.9 GWM 7.9 Kongruenz und Dreiecke
- 1.10 GWM 7.10 Transversalen im Dreieck
- 1.11 GWM 7.11 Besondere Dreiecke
- 1.12 Web-Links
Grundwissen Mathematik 7. Klasse
Diese Fassung muss noch überarbeitet werden!!!
GWM 7.1 Achsensymmetrie
Abbildungsvorschrift der Achsenspiegelung:
Liegen die Punkte und achsensymmetrisch bzgl. der Achse , so gilt:
- ist senkrecht zu
- wird von halbiert.
- Liegt auf der Achse, so ist er mit seinem Spiegelpunkt identisch.
Weitere Eigenschaften der Achsenspiegelung:
- Zueinander symmetrische Strecken sind gleich lang.
- Zueinander symmetrische Winkel sind gleich groß.
- Der Umlaufsinn von Figuren ändert sich.
- Zueinander symmetrische Geraden schneiden sich auf der Achse oder sind parallel
- Speziell: , wenn
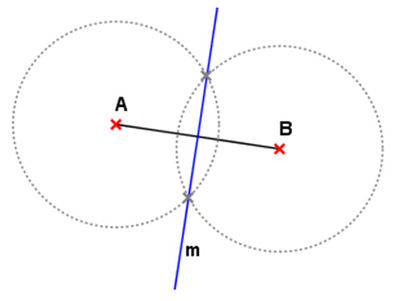
- Die Schnittpunkte zweier (großer) symmetrischer Kreise liegen auf der Achse.
GWM 7.2 Konstruktionen
Konstruktionen der Achsenspiegelung:
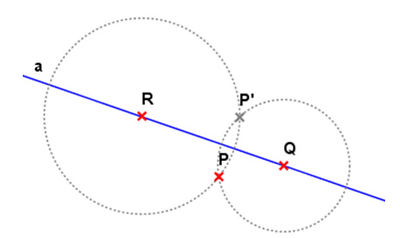
- Spiegelpunkt konstruieren
Wähle zwei beliebige Punkte und auf der Achse . Die Kreise und schneiden sich in und .
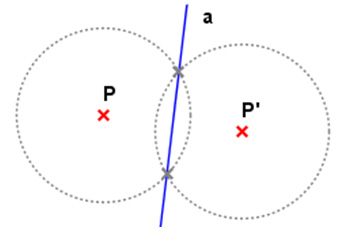
- Achse konstruieren
Zeichne zwei Kreise durch und mit beliebigem (genügend großem), aber gleich großem Radius. Durch die Schnittpunkte der Kreise ist die Achse eindeutig festgelegt.
Konstruktionen mit Hilfe der Achsenspiegelung:
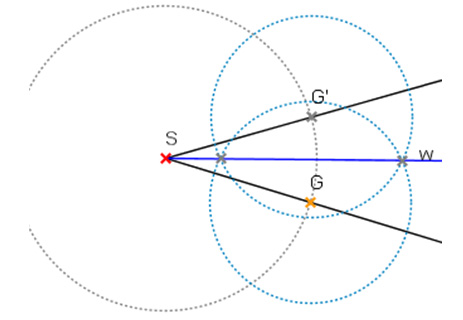
- Winkelhalbierende:
Der Kreis um mit beliebigem Radius schneidet die Schenkel in den Punkten und .Die Symmetrieachse, die auf abbildet und fest lässt ist die Winkelhalbierende.
- Mittelsenkrechte zu :
Die Kreis um und mit gleichem (genügend großem) Radius schneiden sich in zwei Punkten, die die Mittelsenkrechte eindeutig festlegen.
- Lot zu durch fällen
Konstruiere den Spiegelpunkt zu zur Achse . ist das Lot zu .
- Senkrechte in zu errichten
Bestimme zwei beliebige Punkte und auf , die von den gleichen Abstand haben. Die Achse , die auf abbildet (und auch noch durch ) geht ist die Senkrechte zu .
GWM 7.3 Punktsymmetrie
Abbildungsvorschrift der Punktspiegelung:
Liegen die Punkte P und P’ punktsymmetrisch bzgl. des Punktes Z (Zentrum der Spiegelung), so gilt:
- P und P’ sind gleich weit von Z entfernt.
- P, P’ und Z liegen auf einer Geraden.
- Sind P und P’ identisch, so ist P das Zentrum.
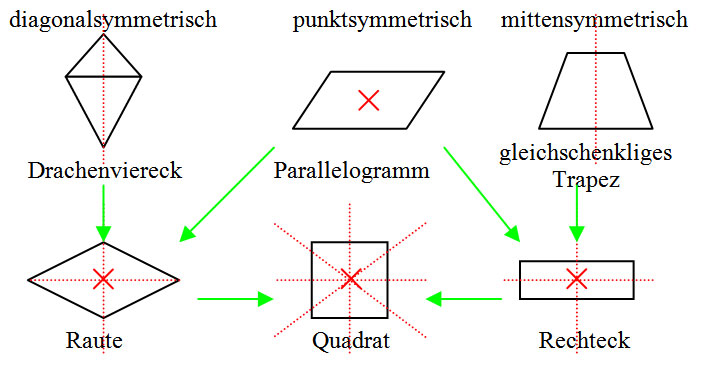
GWM 7.4 Vierecke
Symmetrische Vierecke
GWM 7.5 Winkel
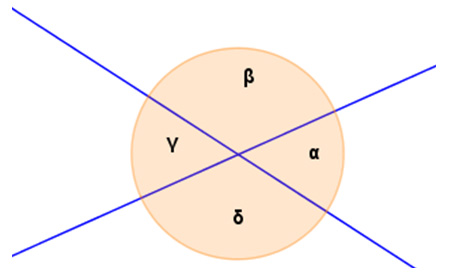
Scheitel- und Nebenwinkel
Scheitelwinkel: und ; und
Nebenwinkel: und ; und
Scheitelwinkel sind gleich groß, Nebenwinkel ergänzen sich zu 180°.
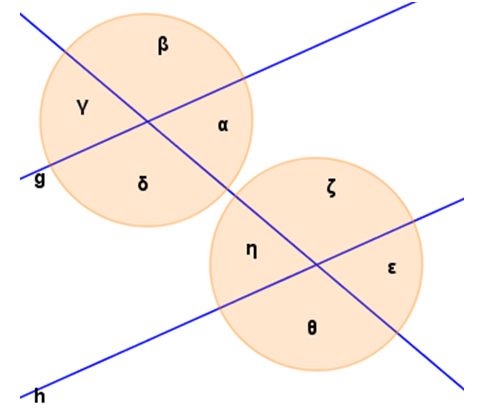
Wechselwinkel, Stufenwinkel, Nachbarwinkel
Wechselwinkel (Z-Winkel): und , und , und , und
Stufenwinkel (F-Winkel): und , und , und , und
Nachbarwinkel (Ergänzungswinkel): und , und
Die Geraden g und h sind genau dann parallel, wenn Wechsel- und Stufenwinkel gleich groß sind, Nachbarwinkel sich zu 180° ergänzen.
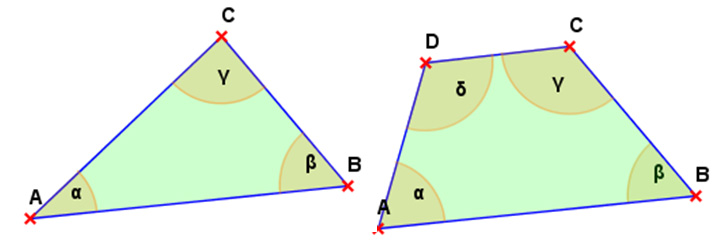
Innenwinkelsumme
Im Dreieck beträgt die Innenwinkelsumme 180°, im Viereck 360°.
GWM 7.6 Terme
Treten in einem Term (Rechenausdruck) verschiedene Variablen (Platzhalter) auf, so dürfen diese mit verschiedenen oder gleichen Zahlen aus der Grundmenge G belegt werden. Man berechnet somit den zugehörigen Termwert.
Zwei Terme heißen äquivalent, wenn sich für alle möglichen Einsetzungen jeweils gleiche Termwerte ergeben. Terme lassen sich durch Termumformungen in äquivalente Terme umwandeln.
Termumformungen:
- Rechengesetze: Assoziativgesetz, Kommutativgesetz, Distributivgesetz (siehe GWM 5.4.)
Klammern auflösen
- Plusklammer: Steht vor einer Klammer ein Pluszeichen, so kann die Klammer weggelassen werden.
- Minusklammer: Steht von einer Klammer ein Minuszeichen, so müssen beim Weglassen der Klammer alle Vorzeichen vertauscht werden. Beispiel: a – (b + c) = a – b – c
Ausmultiplizieren
- Zwei Summen werden multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert (Vorzeichen!) und die Produkte addiert.
Beispiel: (a + b)(c +d) = ac +ad +bc +bd
- Binomische Formeln
Fakorisieren
- Durch Ausklammern gemeinsamer Faktoren oder mit Hilfe der binomischen Formeln kann man Summen in Produkte verwandeln
GWM 7.7 Gleichungen
Wenn man in eine Gleichung an Stelle der Variablen eine Zahl einsetzt, so kann sich eine wahre oder eine falsche Aussage ergeben. In der Lösungsmenge L einer Gleichung sind alle Zahlen aus der Grundmenge G enthalten, die in die Gleichung eingesetzt, eine wahre Aussage ergeben. Eine lineare Gleichung hat entweder genau eine Zahl oder keine Zahl (L = { }) oder alle Zahlen (L = G) der Grundmenge als Lösung.
Äquivalenzumformungen: Äquivalenzumformungen ändern die Lösungsmenge L einer Gleichung nicht. Äquivalenzumformungen sind: Ø Zu (Von) beiden Seiten der Gleichung eine Zahl oder Term addieren (subtrahieren). Ø Beide Seiten der Gleichung mit (durch) einer (eine) Zahl (¹ 0) multiplizieren (dividieren).
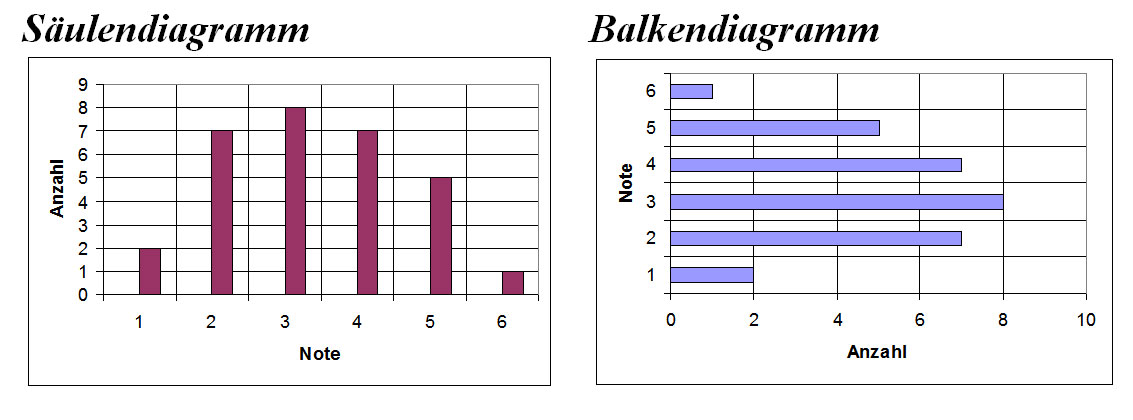
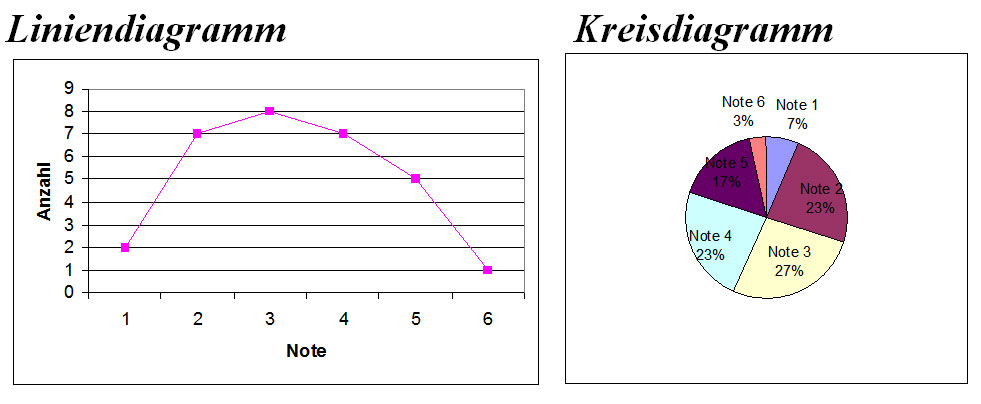
GWM 7.8 Daten, Diagramme
Das arithmetische Mittel (Durchschnitt) einer Datenreihe erhält man, indem man alle Werte addiert und den Summenwert durch die Anzahl der Summanden dividiert.
Verschiedene Diagrammtypen:
GWM 7.9 Kongruenz und Dreiecke
Dreieck sind deckungsgleich (kongruent) bzw. eindeutig konstruierbar, wenn sie in folgenden Größen (Seiten und Winkeln) übereinstimmen bzw. folgende Größen gegeben sind: SSS – Satz: Drei Seiten SWS – Satz: Zwei Seiten und der dazwischen liegende Winkel SsW – Satz: Zwei Seiten und der der größeren Seite gegenüberliegende Winkel WWS – Satz: Zwei Winkel und eine Seite
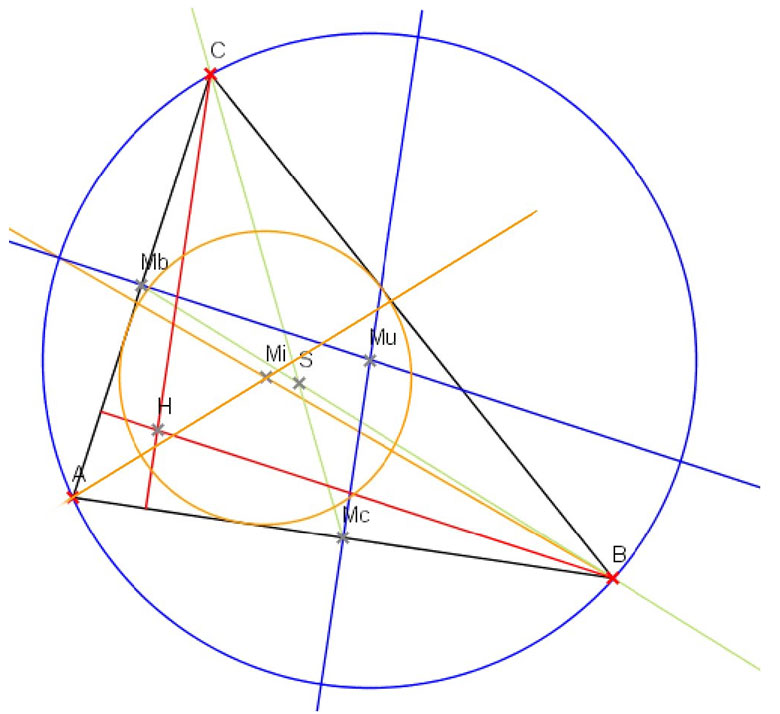
GWM 7.10 Transversalen im Dreieck
Seitenhalbierende (Mitte der Seite und gegenüberliegende Ecke) Alle Seitenhalbierenden eines Dreiecks schneiden sich in genau einem Punkt, dem Schwerpunkt S
Winkelhalbierende (Winkelhalbierende eines Innenwinkels) Alle Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt, dem Inkreismittelpunkt .
Mittelsenkrechte (Senkrechte zum Mittelpunkt einer Seite errichten) Alle Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt, dem Umkreis- mittelpunkt .
Höhe (Lot von Ecke auf gegenüberliegende Seite fällen) Alle Höhen eines Dreiecks schneiden sich in genau einem Punkt H.
GWM 7.11 Besondere Dreiecke
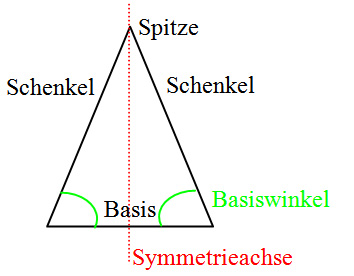
Gleichschenkliges Dreieck:
Dreiecke mit zwei gleich langen Seiten (Schenkeln) heißen gleichschenklig. Die dritte Seite heißt Basis. Eigenschaften: Ø Das Dreieck hat zwei gleich lange Seiten. Ø Das Dreieck hat zwei gleich große Winkel (Basiswinkel). Ø Das Dreieck ist achsensymmetrisch.
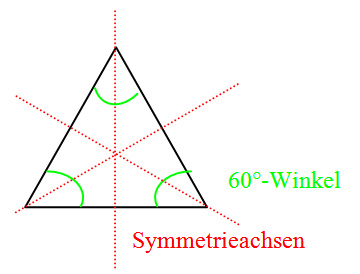
Gleichseitiges Dreieck:
Dreiecke mit drei gleich langen Seiten heißen gleichseitig. Eigenschaften: Ø Das Dreieck hat drei gleich lange Seiten. Ø Das Dreieck hat drei gleich große Winkel (= 60°). Ø Das Dreieck hat drei Symmetrieachsen.
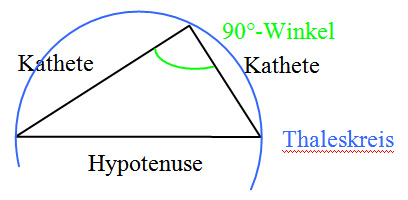
Rechtwinkliges Dreieck:
Dreiecke mit einem 90°-Winkel heißen rechtwinklig. Eigenschaften: Ø Das Dreieck hat einen 90°-Winkel. Ø Der Umkreis des Dreiecks ist der Thaleskreis.
Web-Links





![{\displaystyle [PP']\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2584e58ad3c62b661ae43ac1d5017c9e66e6476c)















![{\displaystyle [AB]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad5e8893865e84b6804c7fba2d2e6e8d068e832)