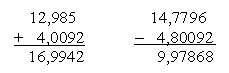GWM6
Inhaltsverzeichnis
- 1 Grundwissen Mathematik 6. Klasse
- 1.1 GWM 6.1 Bruchzahlen / Erweitern und Kürzen
- 1.2 GWM 6.2 Prozent- und Dezimalschreibweise / Rationale Zahlen
- 1.3 GWM 6.3 Vergleichen rationaler Zahlen und Runden
- 1.4 GWM 6.4 Relative Häufigkeit
- 1.5 GWM 6.5 Addieren und Subtrahieren von Brüchen und Dezimalzahlen
- 1.6 GWM 6.6 Multiplikation und Division von Brüchen und Dezimalzahlen
- 1.7 GWM 6.7 Prozentrechnung
- 1.8 GWM 6.8 Flächeninhalt von Dreieck, Parallelogramm und Trapez
- 1.9 GWM 6.9 Oberflächeninhalt und Schrägbild eines Körpers
- 1.10 GWM 6.10 Volumen (Rauminhalt)
- 1.11 Web-Links
Grundwissen Mathematik 6. Klasse
GWM 6.1 Bruchzahlen / Erweitern und Kürzen
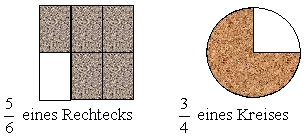
Der Bruchteil eines Ganzen bedeutet: Teile das Ganze in gleiche Teile und nimm von diesen Teilen.
nennt man einen Bruch.
Der Zähler (steht oberhalb des Bruchstriches) gibt an, wie viele dieser Teile zusammengefasst werden, der Nenner (steht unterhalb des Bruchstriches) gibt an, in wie viele Teile das Ganze zerlegt wird.
Beispiel: von 51 € = (51 € : 17) ∙ 12 = 3 € ∙ 12 = 36 €
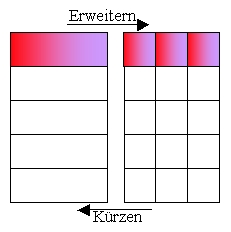
Erweitern: Zähler und Nenner eines Bruches werden mit derselben Zahl multipliziert.
Beispiel: („mit 3 erweitert“)
Kürzen: Zähler und Nenner eines Bruches werden durch dieselbe Zahl dividiert.
Beispiel: („mit 3 gekürzt“)
Ein Bruch ist vollständig gekürzt, wenn Zähler und Nenner keine gemeinsamen Teiler mehr haben.
Beispiel:
Brüche, die durch Kürzen oder Erweitern auseinander hervorgehen, beschreiben den gleichen Bruchteil!
Hauptsatz der Bruchrechnung: Ein Bruch ist ein Quotient. Ein Bruchstrich kann durch ein Divisionszeichen ersetzt werden.
Beispiele:
GWM 6.2 Prozent- und Dezimalschreibweise / Rationale Zahlen
Brüche mit dem Nenner 100 kann man in Prozentschreibweise angeben:
Stellenwerttafel:
| T | H | Z | E | , | z | h | t | zt | ht | m |
| 7 | 2 | 3 | 5 | , | 2 | |||||
| 0 | , | 1 | 7 | 5 | 8 | 9 | 4 |
Brüche, die, vollständig gekürzt, im Nenner nur die Primfaktoren 2 und 5 enthalten, können als endliche Dezimalzahlen geschrieben werden. (Man erweitert auf den Nenner 10, 100, 1000, ...)
Beispiel: (Lies: „Drei Komma null zwei null sieben“)
Brüche kann man auch mit Hilfe der Division in Dezimalbrüche umwandeln:
endlicher Dezimalbruch
unendlicher Dezimalbruch
Alle positiven und negativen Brüche und die Zahl Null bilden zusammen die Menge der rationalen Zahlen .
umfasst auch die Menge aller ganzen Zahlen und damit auch die Menge der natürlichen Zahlen .
GWM 6.3 Vergleichen rationaler Zahlen und Runden
Eine rationale Zahl ist umso größer, je weiter rechts sie sich auf der Zahlengeraden befindet.
Vergleichen von positiven Brüchen: Von zwei Brüchen mit gleichen Nennern ist derjenige größer, der den größeren Zähler besitzt. Von zwei Brüchen mit gleichen Zählern ist derjenige größer, der den kleineren Nenner besitzt.
Um beliebige Bruchzahlen miteinander zu vergleichen, kann durch Kürzen oder Erweitern sowohl der Nenner als auch der Zähler gleich gemacht werden! Dann wendet man die obigen Regeln an.
Vergleichen von Dezimalzahlen: Dezimalzahlen vergleicht man von „links nach rechts“. Die erste Stelle, in der sich zwei Dezimalzahlen unterscheiden, gibt an, welche die größere ist. Beispiel: 42,4530 < 42,4537 < 42,4601 < 42,50
Runden von Dezimalzahlen: Ist die erste wegzulassende Ziffer 0, 1, 2, 3, 4, so wird abgerundet, ist sie 5, 6, 7, 8, 9 so wird aufgerundet.
| Runden auf | 1 Dez | 2 Dez | 3 Dez | 4 Dez | 5 Dez |
GWM 6.4 Relative Häufigkeit
Ein Würfel wurde 200 Mal geworfen. Es wurde notiert, wie oft die Ergebnisse 1; 2; 3; 4; 5 und 6 auftraten.
| Ergebnis | 1 | 2 | 3 | 4 | 5 | 6 |
| Anzahl („Absolute Häufigkeit“) |
38 | 31 | 29 | 33 | 34 | 35 |
| Anteil an der Gesamtzahl („Relative Häufigkeit“) |
In 19 % aller Würfe wurde also die „1“ geworfen.
Führt man dieses Zufallsexperiment „Werfen eines Würfels“ sehr oft durch, kann man damit rechnen, dass die „1“ in etwa aller Würfe fallen wird (nach dem empirischen Gesetz der großen Zahlen).
GWM 6.5 Addieren und Subtrahieren von Brüchen und Dezimalzahlen
Zum Addieren und Subtrahieren müssen Brüche den gleichen Nenner haben.
Der Nenner wird beibehalten, die Zähler werden addiert bzw. subtrahiert.
Brüche mit verschiedenen Nennern müssen durch Kürzen und/oder Erweitern zunächst gleichnamig gemacht werden. Dazu bestimmt man den Hauptnenner der Brüche.
Der Hauptnenner ist das kleinste gemeinsame Vielfache (kgV) der vorliegenden Nenner.
Oder mit Primfaktorzerlegung:
Addieren und Subtrahieren von Dezimalzahlen
Zahlen so untereinanderschreiben, dass Komma unter Komma steht und wie bei natürlichen Zahlen stellenweise rechnen.
GWM 6.6 Multiplikation und Division von Brüchen und Dezimalzahlen
Zwei Brüche werden miteinander multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert (Kürzen nicht vergessen!).
Man dividiert durch einen Bruch, indem man mit seinem Kehrbruch multipliziert (eventuell kann man vor dem Ausmultiplizieren kürzen!).
Multiplizieren von Dezimalzahlen: Zahlen ohne Rücksicht auf die Kommas multiplizieren. Das Komma wird so gesetzt, dass das Ergebnis so viele Nachkommastellen hat wie die Faktoren zusammen.
Dividieren von Dezimalzahlen: Im Divisor und Dividend das Komma so weit nach rechts verschieben, bis der Divisor eine ganze Zahl ist. Überschreitet man im Dividenden das Komma, muss im Ergebnis ein Komma gesetzt werden.
GWM 6.7 Prozentrechnung
Grundwert (GW), Prozentwert (PW) und Prozentsatz (PS) sind die wichtigen Begriffe der Prozentrechnung. Der Grundwert steht für „das Ganze“, also 100 %, der Prozentsatz beschreibt den „Bruchteil“ vom Ganzen als Bruch mit dem Nenner 100 und der Prozentwert gibt an, wie viel dieser „Bruchteil“ als „Anteil“ ausmacht.
Beispiel:
| von | = | |||
| Prozentsatz | Grundwert | Prozentwert |
Berechnung des Prozentsatzes:
Berechnung des Grundwerts:
entspricht
entspricht
entspricht
Berechnung des Prozentwerts:
Allgemein gilt:
GWM 6.8 Flächeninhalt von Dreieck, Parallelogramm und Trapez
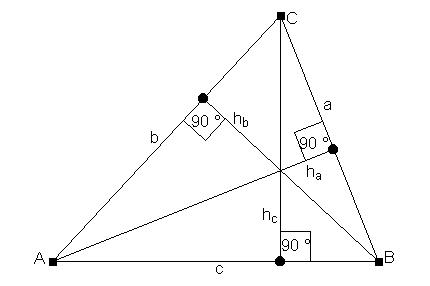
Dreieck
Jedes Dreieck besitzt drei Seiten (Grundlinien). Es ist üblich, diese Seiten mit Kleinbuchstaben, passend zur gegenüberliegenden Ecke zu bezeichnen. Die Länge der senkrechten Verbindungsstrecke zwischen einer Ecke und der gegenüberliegenden Seite (bzw. ihrer Verlängerung) heißt Höhe des Dreiecks. In jedem Dreieck gibt es also drei Höhen.
Für den Flächeninhalt des Dreiecks gilt:
Parallelogramm
Beim Parallelogramm bezeichnet man den Abstand zweier paralleler Seiten als Höhe. In jedem Parallelogramm gibt es also zwei Höhen.
Für den Flächeninhalt des Parallelogramms gilt:
Parallelogramme, die in einer Seite und der zugehörigen Höhe übereinstimmen, haben den gleichen Flächeninhalt.
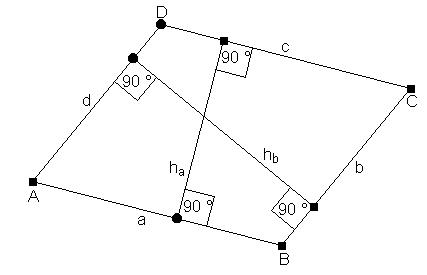
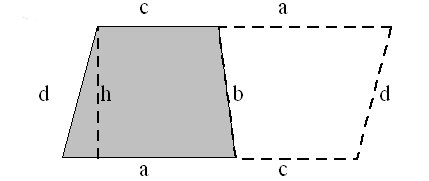
Trapez
Ein Viereck mit zwei zueinander parallelen Seiten nennt man Trapez. Die beiden nicht zueinander parallelen Seiten heißen Schenkel. Der Abstand der zueinander parallelen Seiten heißt Höhe.
Für den Flächeninhalt des Trapezes gilt:
GWM 6.9 Oberflächeninhalt und Schrägbild eines Körpers
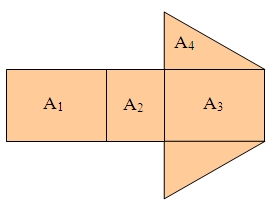
Der Oberflächeninhalt eines Körpers ist identisch mit dem Flächeninhalt seines Netzes. Er berechnet sich als Summe der Flächeninhalte seiner Begrenzungsflächen.
Beispiel:
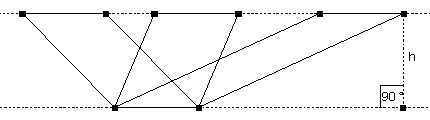
Dreiseitiges gerades Prisma
Oberfläche:
Bemerkung:
Ein gerades Prisma ist ein Körper, bei dem die Grundfläche und die Deckfläche aus
parallelen, deckungsgleichen Vielecken bestehen und die Seitenflächen Rechtecke sind.
Der Flächeninhalt aller Seitenflächen ist das Produkt aus der Höhe des geraden Prismas
und dem Umfang der Grundfläche.
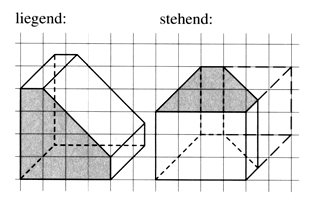
Schrägbild
Die räumliche Darstellung (Perspektive) eines Körpers in der Zeichenebene nennt man Schrägbild des Körpers. Es ist sinnvoll eine Begrenzungsfläche in wahrer Größe zu zeichnen. Kanten, die in Wirklichkeit parallel sind, sind auch im Schrägbild parallel. Senkrechte Kanten dagegen stehen im Schrägbild nicht unbedingt senkrecht aufeinander.
Hinweis: Oft ist es sinnvoll, zunächst das Schrägbild eines Quaders zu zeichnen, aus dem sich das Schrägbild des Körpers dann entwickeln lässt.
GWM 6.10 Volumen (Rauminhalt)
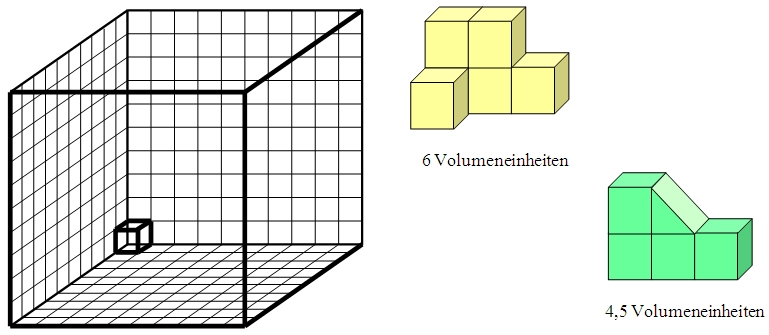
Einen Würfel mit den Kantenlängen 1 LE (Längeneinheit) nennt man Einheitswürfel. Die Anzahl der Einheitswürfel, die notwendig ist, um den Rauminhalt (oder auch das Volumen) eines Körpers vollständig auszufüllen, ist ein Maß für die Größe des Raumes, den ein Körper einschließt.
Volumen: Umrechnungszahl 1000
Besonderheiten:
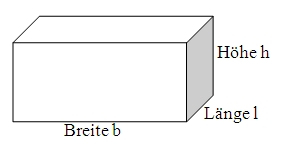
Volumen eines Quaders:
Damit folgt speziell für das Volumen eines Würfels der Kantenlänge a:
Web-Links