SchulheftM5
Mathematik GWM5 SchulheftM6 SchulheftM10 SchulheftM11 SchulheftM12
Inhaltsverzeichnis
- 1 1. Natürliche Zahlen und ihre Darstellungen
- 2 2. Rechnen mit natürlichen Zahlen
- 2.1 2.1 Die Addition natürlicher Zahlen
- 2.2 2.2 Die Subtraktion natürlicher Zahlen
- 2.3 2.3 Verbindung von Addition und Subtraktion
- 2.4 2.4 Die Multiplikation natürlicher Zahlen
- 2.5 2.5 Die Potenzschreibweise, Zehnerpotenzen
- 2.6 2.6 Die Division natürlicher Zahlen
- 2.7 2.7 Verbindung der Grundrechenarten, Distributivgesetz
- 2.8 2.8 Rechnen mit Größen
- 3 3. Ganze Zahlen
- 4 4. Geometrie
- 5 5. Rechnen mit ganzen Zahlen
- 6 6. Berechnungen an ebenen Grundformen
- 7 7. Oberflächen von Körpern
- 8 8. Teilbarkeitslehre
- 8.1 8.1 Teilbarkeit durch Stufenzahlen
- 8.2 8.2 Teilbarkeit durch 2
- 8.3 8.3 Teilbarkeit durch 4
- 8.4 8.4 Teilbarkeit durch 8
- 8.5 8.5 Teilbarkeit durch 25
- 8.6 8.6 Teilbarkeit durch 3
- 8.7 8.7 Teilbarkeit durch 9
- 8.8 8.8 Teilbarkeit durch 6
- 8.9 8.9 Primzahlen
- 8.10 8.10 Die Primfaktorzerlegung natürlicher Zahlen
1. Natürliche Zahlen und ihre Darstellungen
1.1 Natürliche Zahlen sind zum Zählen da!
Die Zahlen, die man zum Zählen benutzt, also 1, 2, 3, 4, 5, 6, ... usw. heißen natürliche Zahlen.
ist die Menge der natürlichen Zahlen.
ist die Menge der ungeraden Zahlen.
ist die Menge der geraden Zahlen.
ist die Menge der Vielfachen von 7.
- Wie viele natürliche Zahlen gibt es?
Antwort: Es gibt unendlich () viele.
(siehe auch Altägyptische Zahlzeichen, Babylonische Zahlen und Indische Ziffern bei Wikipedia)
1.2 Das Zahlensystem der Römer
Die "Ziffern" des Zahlensystem der Römer:
(siehe auch Römische Zahlen bei ZUM.de, Römische und arabische Zahlen ineinander umwandeln und Tabelle mit den römischen Zahlen von 1 bis 1000 von A. Brünner)
1.3 Das Dezimalsystem
Unser Zahlensystem heißt Dezimalsystem oder Zehnersystem. Wir können mit den zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 alle natürlichen Zahlen darstellen.
Das Dezimalsystem ist ein Stellenwertsystem mit der Grundzahl 10, das heißt jede Stelle hat den zehnfachen Wert der Stelle rechts neben ihr.
Die Zahlen 1, 10, 100, 1000, 10000, ... heißen Stufenzahlen des Dezimalsystems.
- Stellenwerttafel:
| B | HMd | ZMd | Md | HM | ZM | M | HT | ZT | T | H | Z | E |
| 3 | 8 | 7 | 2 | 3 | 5 | 4 | 2 | 1 | 5 | 5 | 6 | 8 |
| 5 | 1 | 0 | 4 | 1 | 7 | 5 | 8 | 9 | 4 |
Diese beiden Zahlen heißen:
Drei Billionen achthundertzweiundsiebzig Milliarden dreihundertvierundfünfzig Millionen zweihundertfünfzehntausendfünfhundertachtundsechzig
Fünf Milliarden einhundertvier Millionen einhundertfünfundsiebzigtausendachthundertvierundneunzig
(siehe auch Zahlen in Worten bei Calculino.com)
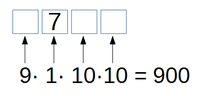
- Beispiel: Wie viele vierstellige Zahlen gibt es, die eine 7 an der Hunderterstelle haben?
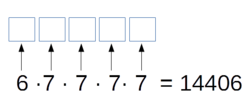
- Beispiel: Wie viele fünfstellige Zahlen gibt es, die nur aus Ziffern kleiner als 7 bestehen?
1.4 Besondere Zahlenmengen
ist die Menge der natürlichen Zahlen.
ist die Menge der natürlichen Zahlen mit Null.
- Die Menge der Vielfachen einer Zahl:
ist die Menge der Vielfachen von 3.
ist die Menge der Vielfachen von 8.
ist die Menge der Vielfachen von 11.
ist die Menge der Vielfachen von 17.
- Die Menge der Teiler einer Zahl:
ist die Menge der Teiler von 16.
ist die Menge der Teiler von 22.
ist die Menge der Teiler von 41.
ist die Menge der Teiler von 50.
(siehe auch Teilermenge bei mathepower.com)
- Die Menge der Primzahlen:
ist die Menge der Zahlen mit genau zwei Teilern.
(siehe auch Primzahlenseite von A.Brünner)
- Die Menge der Quadratzahlen:
ist die Menge der Zahlen, die man erhält, wenn man natürliche Zahlen mit sich selbst multipliziert.
Eine Menge ist eine Zusammenfassung verschiedener Dinge. Jedes Ding darf nur einmal vorkommen und die Reihenfolge spielt keine Rolle.
Die einzelnen Dinge in einer Menge nennt man Elemente.
Zum Beispiel ist die Zahl 7 ein Element der natürlichen Zahlen, jedoch kein Element der Menge der geraden Zahlen.
Schreibweise:
: "ist Element von"
: "ist kein Element von"
Beispiele:
1.5 Die Anordnung der natürlichen Zahlen
Die natürlichen Zahlen sind der Größe nach geordnet:
- Zahlenstrahl:
Größere Zahlen stehen auf dem Zahlenstrahl weiter rechts, kleinere Zahlen weiter links.
- Anordnungszeichen:
"kleiner als"
"größer als"
"kleiner oder gleich als"
"größer oder gleich als"
In Diagrammen kann man mit Hilfe des Zahlenstrahls ablesen, welchen Wert eine bestimmte Größe hat.
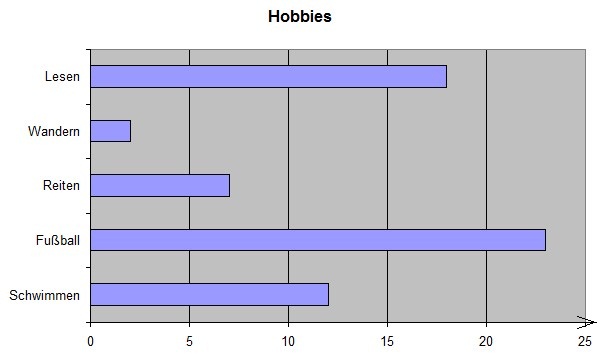
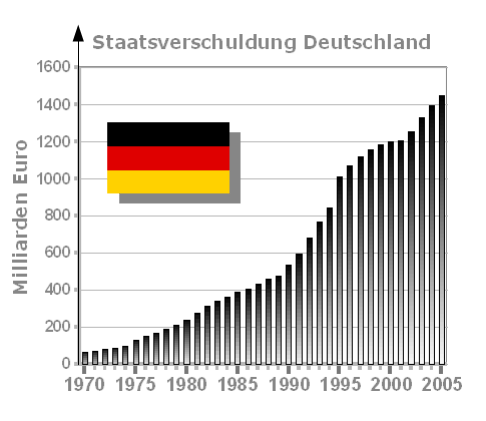
- Balken- bzw. Säulendiagramm
1.6 Das Runden von natürlichen Zahlen
Man rundet eine Zahl auf eine bestimmte Stelle, indem man die nachfolgende Ziffer dieser Stelle betrachtet:
- Ist diese Ziffer kleiner oder gleich 4, so wird abgerundet.
- Ist diese Ziffer größer oder gleich 5, so wird aufgerundet.
(siehe auch zum Üben Runden mit natürlichen Zahlen bei interaktiv-lernen.net)
- Beispiel: Wie viele natürliche Zahlen ergeben gerundet auf die Zehntausenderstelle die Zahl 543700000? Wie heißt die kleinste und die größte dieser Zahlen?
Antwort: Es sind 10000 Zahlen. Die kleinste dieser Zahlen ist 543695000 und die größte ist 543704999.
2. Rechnen mit natürlichen Zahlen
2.1 Die Addition natürlicher Zahlen
(siehe auch Schriftliche Addition bei mathepower.com)
- Kommutativgesetz (Vertauschungsgesetz):
Vertauscht man die Summanden einer Summe, so ändert sich der Wert der Summe nicht.
Z. B. :
- Assoziativgesetz (Verbindungsgesetz):
In Summen kann man die Klammern umsetzen oder weglassen, ohne dass sich der Wert der Summe ändert.
Z. B. :
2.2 Die Subtraktion natürlicher Zahlen
(siehe auch Schriftliches Subtrahieren bei mathetools.de oder Schriftlich subtrahieren bei Calculino.com)
Die Addition einer Zahl wird durch die Subtraktion der gleichen Zahl wieder rückgängig gemacht. Die Subtraktion ist also die Umkehrung der Addition.
- Besonderheiten der Subtraktion: Für die Subtraktion gilt weder das Kommutativgesetz noch das Assoziativgesetz!
2.3 Verbindung von Addition und Subtraktion
| Rechenausdrücke ohne Klammern werden von links nach rechts berechnet! |
Z. B. :
| Was in Klammern steht wird zuerst berechnet! |
Z. B. :
| Ineinander geschachtelte Klammern berechnet man von innen nach außen! |
Z. B. :
2.4 Die Multiplikation natürlicher Zahlen
Die Addition gleicher Summanden kann als Multiplikation kürzer geschrieben werden:
Z. B. :
(siehe auch Schriftliche Multiplikation bei mathepower.com)
- Besonderheiten der Multiplikation:
Mal Eins verändert den Wert eines Produktes nicht!
Mal Null macht den Wert eines Produktes immer zu Null!
- Kommutativgesetz (Vertauschungsgesetz):
Vertauscht man die Faktoren, so ändert sich der Wert des Produktes nicht.
Z. B. :
- Assoziativgesetz (Verbindungsgesetz):
Bei Produkten kann man die Klammern umsetzen oder weglassen, ohne dass sich der Wert des Produktes ändert.
Z. B. :
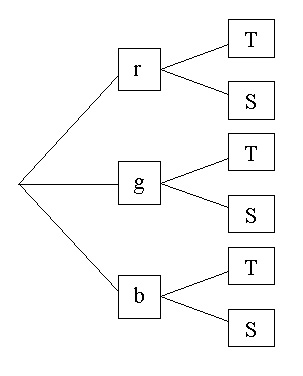
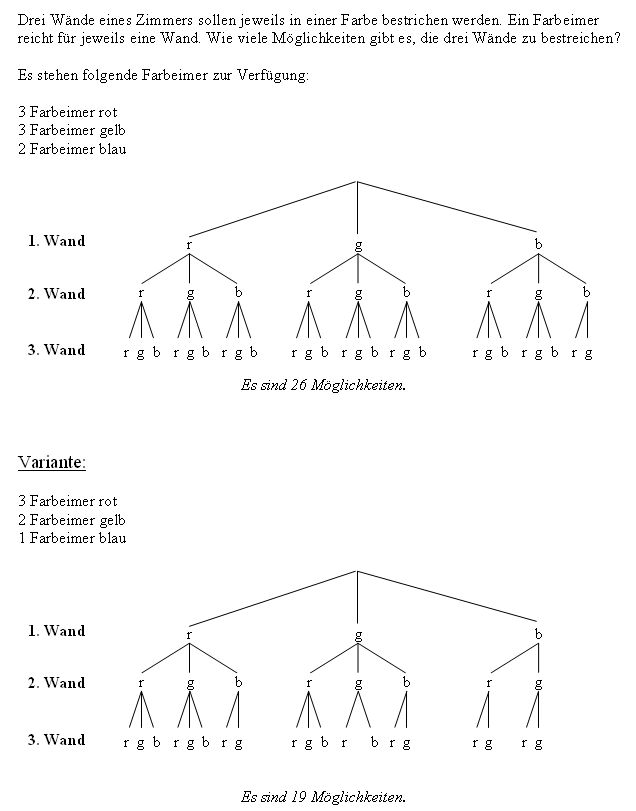
- Baumdiagramme
Jeder Pfad durch den Baum steht für eine Kombinationsmöglichkeit.
Beispiel: Es gibt rote (r), grüne (g) und blaue (b) Schuluniformen. Sie sind als T-Shirt T oder Sweatshirt S erhältlich.
Dann gibt es Möglichkeiten, nämlich: rT, gT, bT, rS, gS, bS.
Weitere Beispiele:
2.5 Die Potenzschreibweise, Zehnerpotenzen
Potenz:
Z. B. :
Merke: aber
- Zehnerpotenzen:
| Name | Zahl in Dezimalschreibweise | Zahl in Potenzschreibweise |
| Eins | 1 | |
| Zehn | 10 | |
| Hundert | 100 | |
| Tausend | 1 000 | |
| Zehntausend | 10 000 | |
| Hunderttausend | 100 000 | |
| Eine Million | 1 000 000 | |
| Zehn Millionen | 10 000 000 | |
| Hundert Millionen | 100 000 000 | |
| Eine Milliarde | 1 000 000 000 |
- Zweierpotenzen:
| Potenzschreibweise | |||||||||||
| Dezimalschreibweise | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
- Quadratzahlen:
| Potenzschreibweise | |||||||||||||||||||||||||
| Dezimalschreibweise | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 |
2.6 Die Division natürlicher Zahlen
(siehe auch Schriftliches Dividieren von A. Brünner)
Die Multiplikation einer Zahl wird durch die Division der gleichen Zahl wieder rückgängig gemacht. Die Division ist also die Umkehrung der Multiplikation.
- Besonderheiten der Division: Für die Division gilt weder das Kommutativgesetz noch das Assoziativgesetz!
Geteilt durch Eins verändert den Wert des Quotienten nicht!
Null geteilt durch irgendeine Zahl bleibt Null!
Aber Achtung:
| Durch Null kann und darf man nicht dividieren! |
2.7 Verbindung der Grundrechenarten, Distributivgesetz
Wichtige "Vorfahrtsregel":
| Klammer vor Potenz vor Punkt vor Strich! |
Was in Klammern steht, wird zuerst berechnet. Danach gehen die Potenzrechnungen vor Punktrechnungen (Multiplikation und Division) und diese widerum vor Strichrechnungen (Addition und Subtraktion).
(siehe auch Klammeraufgaben bei mathepower.com)
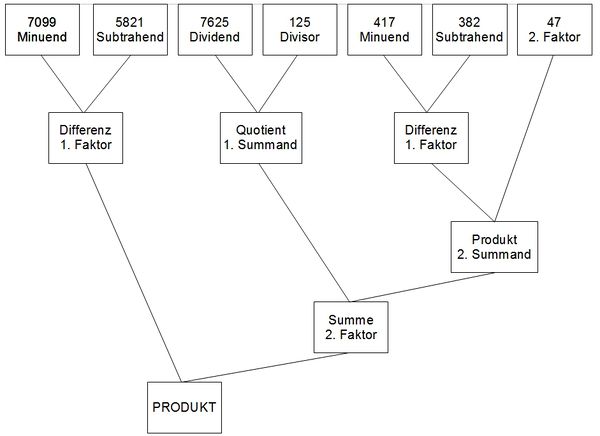
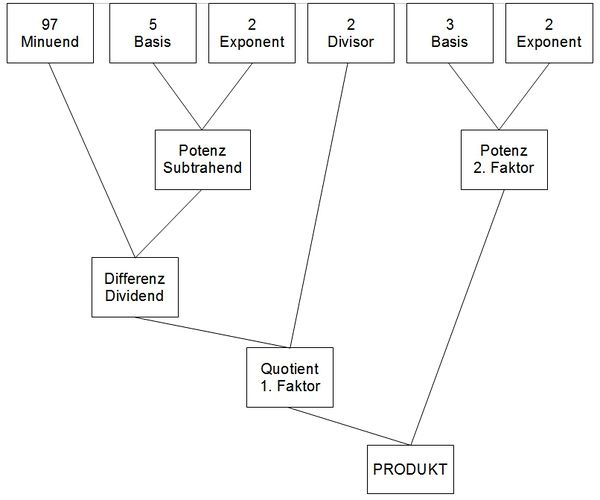
- Gliederung von Termen:
Beispiele:
- Distributivgesetz (Verteilungsgesetz):
Eine Summe (bzw. Differenz) wird mit einer Zahl multipliziert, indem man jedes Glied mit der Zahl multipliziert und die Produktwerte addiert (bzw. subtrahiert).
Eine Summe (bzw. Differenz) wird durch eine Zahl dividiert, indem man jedes Glied durch die Zahl dividiert und die Quotientenwerte addiert (bzw. subtrahiert).
- Das große Einmaleins
| · | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
(für alle Grundrechenarten und zum Üben: Natürliche Zahlen bei mathepower.de)
2.8 Rechnen mit Größen
(Zum Üben siehe auch Umwandeln von Einheiten von A. Brünner oder Größen bei mathepower.de)
Längen
Umrechnungszahl , Ausnahme:
Geldwerte
Umrechnungszahl
Massen
Umrechnungszahl
Zeiten
Maßstab
Der Maßstab (lies 1 zu 100) bedeutet: in der Zeichnung entspricht in der Wirklichkeit.
Beispiel:
Eine lange Strecke in einer Karte mit dem Maßstab entspricht in der Wirklichkeit .
3. Ganze Zahlen
3.1 Zahlengerade
Betrag: Der Betrag einer Zahl ist ihre Entfernung vom Nullpunkt.
Beispiel:
Zahlen, die gleichen Betrag aber verschiedene Vorzeichen haben, heißen Gegenzahlen.
Beispiel:
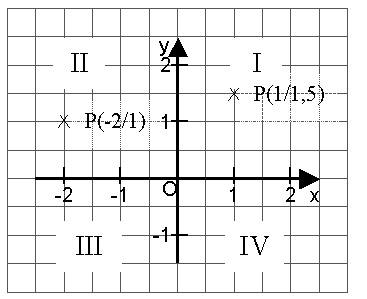
3.2 Das Koordinatensystem
Ein Koordinatensystem besteht aus zwei senkrechten Zahlenstrahlen mit gemeinsamem Nullpunkt. Die x-Achse heißt auch Abszisse, die y-Achse auch Ordinate.
Ein Punkt P(x/y) ist durch seine Koordinaten festgelegt.
Die Ebene wird in vier Quadranten unterteilt.
4. Geometrie
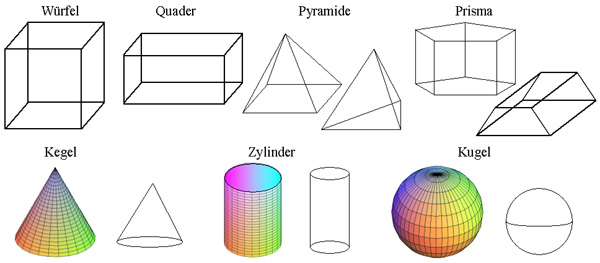
4.1 Räumliche Grundformen - Körper
Der Würfel ist ein Spezialfall des Quaders. Der Quader ist ein Spezialfall des Prismas.
4.2 Geometrische Grundbegriffe
Punkte
Punkte (z.B Eckpunkte von Körpern) kennzeichnen wir mit großen Buchstaben, z.B. :
Strecken
Eine gerade Linie zwischen zwei Punkten heißt Strecke. Diese kennzeichnen wir mit Hilfe der beiden Endpunkte:
Die Länge einer Strecke bezeichnen wir mit:
Geraden
Durch zwei Punkte wird eine Gerade festgelegt. Kennzeichnung:
Halbgeraden
Verlängert man eine Strecke über einen Endpunkt hinaus geradlinig unendlich weit, so entsteht eine Halbgerade. Kennzeichnung:
Zueinander senkrecht
Strecken oder Geraden sind zueinander senkrecht, wenn sie sich unter einem rechten Winkel schneiden.
Eine Strecke, Gerade oder Halbgerade, die zu einer anderen sekrecht ist, nennt man auch Lot zu der anderen.
Zueinander parallel
Zwei verschiedene Geraden sind genau dann zueinander parallel, wenn sie sich nie schneiden.
Kreise
Alle Punkte, die von einem Punkt die gleiche Entfernung haben, liegen auf dem Kreis um diesen Punkt, wobei die Entfernung der Radius des Kreises ist.
Der Durchmesser ist doppelt so lang wie der Radius.
Winkel
Ein Winkel besteht aus zwei Halbgeraden ("Schenkel") mit gemeinsamen Anfangspunkt ("Scheitel"). Die beiden Halbgeraden schließen das zum Winkel gehörige Winkelfeld ein.
Achsensymmetrie
Figuren, die sich so falten lassen, dass die beiden Hälften genau aufeinander passen, heißen achsensymmetrische Figuren. Die Faltgerade nennt man Symmetrieachse.
Die Verbindungsstrecke zweier symmetrischer Punkte wird durch die dazu senkrechte Symmetrieachse halbiert.
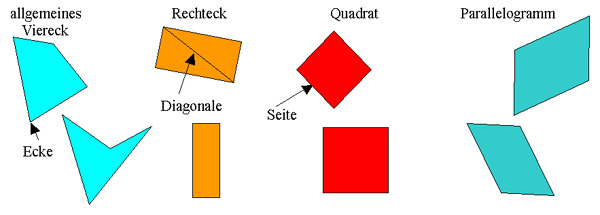
Vielecke und besondere Vierecke
Rechteck
Ein Rechteck ist ein Viereck mit vier rechten Winkeln. Gegenüberliegende Seiten sind gleich lang und parallel. Die Diagonalen sind gleich lang und halbieren sich gegenseitig.
Quadrat
Ein Quadrat ist ein Rechteck mit vier gleich langen Seiten. Die Diagonalen stehen aufeinander senkrecht.
Parallelogramm
Ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten zueinander parallel sind.
Raute
Eine Raute ist ein Parallelogramm mit vier gleich langen Seiten.
5. Rechnen mit ganzen Zahlen
5.1 Addieren und Subtrahieren von ganzen Zahlen
Beispiele:
Regeln:
5.2 Multiplizieren von ganzen Zahlen
Beispiele:
Regeln:
| "positiv mal positiv = positiv" | "positiv mal negativ = negativ" | "negativ mal positiv = negativ" | "negativ mal negativ = positiv" |
5.3 Dividieren von ganzen Zahlen
Beispiele:
Regeln:
| "positiv durch positiv = positiv" | "positiv durch negativ = negativ" | "negativ durch positiv = negativ" | "negativ durch negativ = positiv" |
6. Berechnungen an ebenen Grundformen
6.1 Umfang von Dreieck, Rechteck und Quadrat
Der Umfang einer ebenen Figur ist die Gesamtlänge aller Begrenzungslinien um die Figur herum.
Der Umfang eines Dreiecks mit den Seitenlängen a, b und c ist:
Der Umfang eines Rechtecks mit der Breite b und der Länge l ist:
Der Umfang eines Quadrats mit der Seitenlänge a ist:
6.2 Flächeninhalte
Flächeneinheiten:
Umrechnungszahl
Achtung:
(Zum Üben siehe auch Umwandeln von Einheiten von A. Brünner oder Größen bei mathepower.de)
Die Flächenformel des Rechtecks:
Die Flächenformel des Quadrats:
7. Oberflächen von Körpern
Die Oberfläche eines Körpers ist die Summe aller seiner Begrenzungsflächen.
| Oberfläche des Quaders: |
| Oberfläche des Würfels: |
8. Teilbarkeitslehre
Schreibweise:
a|b bedeutet: Die Zahl a ist ein Teiler von b (sprich: "a teilt b").
Beispiele: 3|12; 15|60; 11|1001; 25|1025;
(siehe auch Teilbarkeitslehre bei mathepower.de)
8.1 Teilbarkeit durch Stufenzahlen
| Eine Zahl ist durch eine Stufenzahl teilbar, wenn sie mindestens so viele Nullen am Ende hat wie die Stufenzahl. |
Beispiele: 10|56200; 100|6700; 1000|510100000; 10000|33020000;
| Alle Stufenzahlen sind durch 2 und durch 5 teilbar. |
8.2 Teilbarkeit durch 2
| Eine Zahl ist durch 2 teilbar, wenn sie eine gerade Zahl ist. |
Beispiele: 2|18; 2|6033446; 2|106; 2|10254;
8.3 Teilbarkeit durch 4
| Eine Zahl ist durch 4 teilbar, wenn ihre letzten beiden Ziffern eine durch 4 teilbare Zahl bilden oder 2 Nullen sind. |
Beispiele: 4|44512; 4|77600; 4|344144; 4|7128;
8.4 Teilbarkeit durch 8
| Eine Zahl ist durch 8 teilbar, wenn ihre letzten drei Ziffern eine durch 8 teilbare Zahl bilden oder 3 Nullen sind. |
Beispiele: 8|44000; 8|77400; 8|344152; 8|7632;
8.5 Teilbarkeit durch 25
| Eine Zahl ist durch 25 teilbar, wenn sie auf 25, 50, 75 oder 00 endet. |
Beispiele: 25|445125; 25|77600; 25|344150; 25|7175;
8.6 Teilbarkeit durch 3
| Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist. |
Beispiele: 3|44502; 3|77610; 3|144; 3|7128;
8.7 Teilbarkeit durch 9
| Eine Zahl ist durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist. |
Beispiele: 9|44532; 9|77607; 9|396; 9|7128;
8.8 Teilbarkeit durch 6
| Eine Zahl ist durch 6 teilbar, wenn sie durch 2 und durch 3 teilbar ist. |
Beispiele: 6|44502; 6|77610; 6|144; 6|7128;
8.9 Primzahlen
| Eine Primzahl ist eine natürliche Zahl, die genau zwei Teiler hat. |
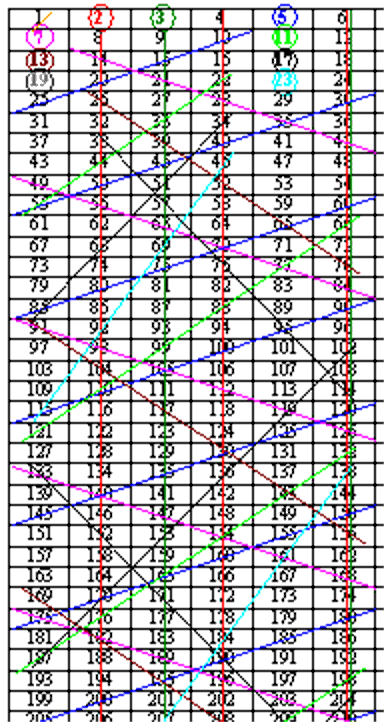
Sieb des Eratosthenes zur Primzahlsuche bis 200
Primzahlen bis 10000:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919, 7927, 7933, 7937, 7949, 7951, 7963, 7993, 8009, 8011, 8017, 8039, 8053, 8059, 8069, 8081, 8087, 8089, 8093, 8101, 8111, 8117, 8123, 8147, 8161, 8167, 8171, 8179, 8191, 8209, 8219, 8221, 8231, 8233, 8237, 8243, 8263, 8269, 8273, 8287, 8291, 8293, 8297, 8311, 8317, 8329, 8353, 8363, 8369, 8377, 8387, 8389, 8419, 8423, 8429, 8431, 8443, 8447, 8461, 8467, 8501, 8513, 8521, 8527, 8537, 8539, 8543, 8563, 8573, 8581, 8597, 8599, 8609, 8623, 8627, 8629, 8641, 8647, 8663, 8669, 8677, 8681, 8689, 8693, 8699, 8707, 8713, 8719, 8731, 8737, 8741, 8747, 8753, 8761, 8779, 8783, 8803, 8807, 8819, 8821, 8831, 8837, 8839, 8849, 8861, 8863, 8867, 8887, 8893, 8923, 8929, 8933, 8941, 8951, 8963, 8969, 8971, 8999, 9001, 9007, 9011, 9013, 9029, 9041, 9043, 9049, 9059, 9067, 9091, 9103, 9109, 9127, 9133, 9137, 9151, 9157, 9161, 9173, 9181, 9187, 9199, 9203, 9209, 9221, 9227, 9239, 9241, 9257, 9277, 9281, 9283, 9293, 9311, 9319, 9323, 9337, 9341, 9343, 9349, 9371, 9377, 9391, 9397, 9403, 9413, 9419, 9421, 9431, 9433, 9437, 9439, 9461, 9463, 9467, 9473, 9479, 9491, 9497, 9511, 9521, 9533, 9539, 9547, 9551, 9587, 9601, 9613, 9619, 9623, 9629, 9631, 9643, 9649, 9661, 9677, 9679, 9689, 9697, 9719, 9721, 9733, 9739, 9743, 9749, 9767, 9769, 9781, 9787, 9791, 9803, 9811, 9817, 9829, 9833, 9839, 9851, 9857, 9859, 9871, 9883, 9887, 9901, 9907, 9923, 9929, 9931, 9941, 9949, 9967, 9973
| Um herauszufinden, ob eine Zahl eine Primzahl ist, untersucht man sie darauf, ob sie durch kleinere Primzahlen teilbar ist.
Findet man bis zu der Primzahl, die mit sich selbst multipliziert ein bereits größeres Ergebnis als die Zahl selbst liefert, dabei keinen weiteren Teiler, so ist diese Zahl eine Primzahl. |
(siehe auch Primzahlenseite von A.Brünner)
8.10 Die Primfaktorzerlegung natürlicher Zahlen
Alle natürlichen Zahlen (außer die Primzahlen selbst) lassen sich als Produkt von Primzahlen schreiben. Dieses Produkt heißt die Primfaktorzerlegung der Zahl und die Faktoren heißen Primfaktoren.
Beispiele:
Schreibform, um die Primfaktorzerlegung größerer Zahlen ausfindig zu machen:
(siehe auch Primfaktorzerlegung auf der Primzahlenseite von A.Brünner)
Mathematik GWM5 SchulheftM6 SchulheftM10 SchulheftM11 SchulheftM12




































![{\displaystyle 126+\{311-[56-(12-5)]\}=126+\{311-[56-7]\}=126+\{311-49\}=126+262=388\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6691e341820f7012ee07faf88df6b1f69f6e2064)





























































![{\displaystyle (7099-5821)\cdot [7625:125+(417-382)\cdot 47]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d47f683a8762acb982361d47750dcbdf488d36c0)

























![{\displaystyle [AB]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad5e8893865e84b6804c7fba2d2e6e8d068e832)