GWM5

Grundwissen Mathematik 5. Klasse

GWM 5.1 Zahlenmengen

$\mathbb {N} =\{1,2,3,4,5,6,7,8,9,10,11,12,...\}$ Menge der natürlichen Zahlen

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 991250722
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$\mathbb {N} _{0}=\{0,1,2,3,4,5,6,7,8,9,10,11,...\}$ Menge der natürlichen Zahlen mit Null

$\mathbb {Z} =\{...-4,-3,-2,-1,0,1,2,3,4,...\}$ Menge der ganzen Zahlen

Primzahlen: Eine Zahl die genau zwei Teiler hat, heißt Primzahl.

Menge der Primzahlen

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 996423789
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$=\{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,\$

$73,79,83,89,97,101,103,107,109,113,127,131,...\}\$

Primfaktorzerlegung: Jede Zahl lässt sich eindeutig in ein Produkt von Primzahlen zerlegen.

Beispiel: $60=2\cdot 30=2\cdot 2\cdot 15=2\cdot 2\cdot 3\cdot 5=2^{2}\cdot 3\cdot 5$

Menge der Quadratzahlen

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993542032
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$=\{1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,\$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993473103
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$324,361,400,441,484,529,576,625,...\}\$

Römische Zahlen:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 997437981
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$I=1;\ V=5;\ X=10;\ L=50;\ C=100;\ D=500;\ M=1000$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 991250726
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$I,\ X,\ C,\ M$ dürfen bis zu dreimal nacheinander stehen.

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 997935628
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$I,\ X,\ C$ werden beim Voranstellen einmal abgezogen.

Beispiel:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 963607889
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$MCMXCIV=1994;\ MMMDCCCLXXXVIII=3888$

GWM 5.2 Fachbegriffe beim Rechnen

Addition:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1001332241
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}171&+&19&=&190\\{\rm {1.\ Summand}}&+&{\rm {2.\ Summand}}&=&{\rm {Wert\ der\ Summe}}\end{matrix}}$

Subtraktion:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 999698128
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}190&-&19&=&171\\{\rm {Minuend}}&-&{\rm {Subtrahend}}&=&{\rm {Wert\ der\ Differenz}}\end{matrix}}$

Multiplikation:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 996423791
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}125&\cdot &8&=&1000\\{\rm {1.\ Faktor}}&\cdot &{\rm {2.\ Faktor}}&=&{\rm {Wert\ des\ Produkts}}\end{matrix}}$

Division:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 999698130
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}1000&:&8&=&125\\{\rm {Dividend}}&:&{\rm {Divisor}}&=&{\rm {Wert\ des\ Quotienten}}\end{matrix}}$

GWM 5.3 Potenzen

Potenz:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1010206835
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a\cdot a\cdot a\cdot a\cdot a\cdot a=a^{6}$

Beispiel:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 992432155
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4=4^{7}$

Merke:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 963607891
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$2^{3}=8\$ aber

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 994689548
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$2\cdot 3=6$

Potenz:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 997935633
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}3^{5}&=&243\\{\rm {Basis}}^{\rm {Exponent}}&=&{\rm {Wert\ der\ Potenz}}\end{matrix}}$

GWM 5.4 Rechengesetze und die Bedeutung der Null

Reihenfolge: „Klammer vor Potenz vor Punkt vor Strich!“

Was noch nicht zum Rechnen dran ist, schreibt man unverändert an!

Kommutativgesetz:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 991938916
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a\cdot b=b\cdot a\qquad 5\cdot 3=3\cdot 5$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993542034
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a+b=b+a\qquad 5+3=3+5$

Assoziativgesetz:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993473106
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(a+b)+c=a+(b+c)=a+b+c\qquad (2+3)+5=2+(3+5)=2+3+5$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 999698133
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(a\cdot b)\cdot c=a\cdot (b\cdot c)=a\cdot b\cdot c\qquad (2\cdot 3)\cdot 5=2\cdot (3\cdot 5)=2\cdot 3\cdot 5$

Distributivgesetz:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1006378499
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a\cdot (b+c)=a\cdot b+a\cdot c\qquad 2\cdot (5+3)=2\cdot 5+2\cdot 3$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 991938918
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a\cdot (b-c)=a\cdot b-a\cdot c\qquad 2\cdot (5-3)=2\cdot 5-2\cdot 3$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1006378501
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(a+b):c=a:c+b:c\qquad (170+51):17=170:17+51:17$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1001332243
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(a-b):c=a:c-b:c\qquad (170-51):17=170:17-51:17$

Null bei der Multiplikation:

Ist ein Faktor Null, so ist auch der Produktwert Null.

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1007785647
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$3\cdot 0=0\cdot 3=0$

Ist der Produktwert Null, so muss mindestens ein Faktor Null sein!

Aus

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 994689550
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a\cdot b=0$ folgt:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1005492892
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$a=0\$ oder

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993892544
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$\ b=0$.

Null bei der Division:

Allgemein:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1007785649
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$0:a=0\quad (a\neq 0)\qquad 0:5=0$

Die Division durch Null ist nicht erlaubt!

GWM 5.5 Ganze Zahlen

Zahlengerade:

Betrag: Der Betrag einer Zahl ist ihre Entfernung vom Nullpunkt.

Beispiel:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1001332249
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$|-4|=4;\ |4|=4$

Zahlen, die gleichen Betrag aber verschiedene Vorzeichen haben, heißen Gegenzahlen.

Beispiel:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1001332245
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$4\leftrightarrow -4;\ 3\leftrightarrow -3$

GWM 5.6 Rechnen mit ganzen Zahlen: Addition und Subtraktion

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 988411237
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(+11)+(-4)=11-4=7\$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1006378503
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$(+11)-(+4)=11-4=7\$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1010206837
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$5+(+3)=5+3=8\qquad -5+(+3)=-5+3=-2$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 992432157
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$5+(-3)=5-3=2\qquad -5+(-3)=-5-3=-8$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993473108
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$5-(+3)=5-3=2\qquad -5-(+3)=-5-3=-8$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 999698135
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$5-(-3)=5+3=8\qquad -5-(-3)=-5+3=-2$

GWM 5.7 Rechnen mit ganzen Zahlen: Multiplikation und Division

Regel: Gleiche Vorzeichen ergeben beim Multiplizieren und Dividieren "

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 996423793
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$+\$", ungleiche "

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1001332247
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$-\$".

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1009748146
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$3\cdot (+5)=15\quad 15:(+5)=3\quad -3\cdot (+5)=-15\quad -15:(+5)=-3$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 991743955
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$3\cdot (-5)=-15\quad 15:(-5)=-3\quad -3\cdot (-5)=15\quad -15:(-5)=3$

GWM 5.8 Größen und Maßstab

Länge:

Umrechnungszahl

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 988411239
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$10\$, Ausnahme:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1004777536
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$1~km=1000~m;\$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 996423796
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}1~m=10~dm;\quad \ &1~dm=10~cm;&1~cm=10~mm;\qquad \qquad \ \ \\1~m=0,001~km;&1~dm=0,1~m;&1~cm=0,1~dm=0,01~m;\end{matrix}}$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1007329029
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:24 GMT


Sensitive client information

IP address: 188.64.62.105

$1~mm=0,1~cm=0,01~dm=0,001~m;\$

Fläche:

Umrechnungszahl

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 990654502
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$100\$, Achtung:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 981006043
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1~km^{2}=1~km\cdot 1~km=1000~m\cdot 1000~m=1000000~m^{2}$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 985093116
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}1~km^{2}=100~ha;&1~ha=100~a;\quad \ \ &1~a=100~m^{2};\qquad \qquad \qquad \quad \\&1~ha=0,01~km^{2};&1~a=0,01~ha=0,0001~km^{2};\end{matrix}}$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 988246921
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}1~m^{2}=100~dm^{2};\qquad \qquad \quad &1~dm^{2}=100~cm^{2};&1~cm^{2}=100~mm^{2};\\1~m^{2}=0,01~a=0,0001~ha;&1~dm^{2}=0,01~m^{2};&1~cm^{2}=0,01~dm^{2};\end{matrix}}$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 990795794
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1~mm^{2}=0,01~cm^{2};$

Masse:

Umrechnungszahl

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1002387285
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1000\$

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 985093118
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

${\begin{matrix}1~t=1000~kg;&1~kg=1000~g;&1~g=1000~mg;&\\&1~kg=0,001~t;&1~g=0,001~kg;&1~mg=0,001~g;\end{matrix}}$

Zeit:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 990654504
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1~a=365~d;\quad 1~d=24~h;\quad 1~h=60~min;\quad 1~min=60~s;$

Maßstab:

Der Maßstab

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1009648647
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1:100\$ (lies 1 zu 100) bedeutet: $1~cm$ in der Zeichnung entspricht

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008539922
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$100~cm$ in der Wirklichkeit.

Beispiel:

Eine

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 988246923
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$5~cm$ lange Strecke in einer Karte mit dem Maßstab

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1002387287
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$1:250000\$ entspricht in der Wirklichkeit

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1002387289
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$5\cdot 250000~cm=1250000~cm=12500~m=12,5~km$.

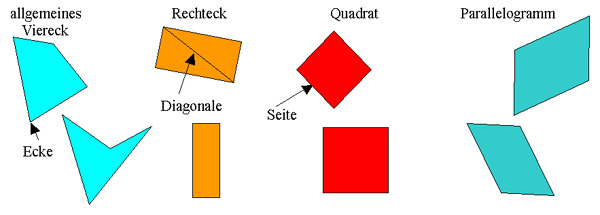
GWM 5.9 Kreis Vierecke

Alle Punkte, die von einem Punkt M aus gleich weit entfernt sind, liegen auf einem Kreis.

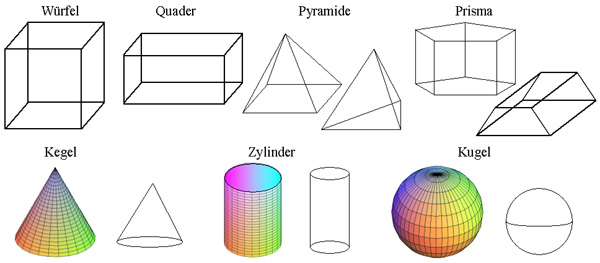
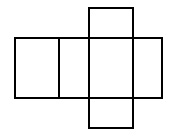
GWM 5.10 Körper

GWM 5.11 Umfang, Flächeninhalt, Oberflächen

Umfang des Rechtecks: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 1009092996 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $U_{R}=2\cdot (l+b)\qquad$	Umfang des Quadrates: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 988411265 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $U_{Q}=4\cdot a$
Flächeninhalt des Rechtecks: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 996585979 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $A_{R}=l\cdot b$	Flächeninhalt des Quadrates: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 996585981 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $A_{Q}=a^{2}\$
Oberfläche des Quaders: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 1006117264 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $O_{Q}=2\cdot (l\cdot b+l\cdot h+b\cdot h)$	Oberfläche des Würfels: Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp3066 cp3066, Varnish XID 990795796 Upstream caches: cp3066 int Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT Sensitive client information IP address: 188.64.62.105 $O_{W}=6\cdot a^{2}\$

Netz des Quaders:

GWM 5.12 Strecken, Geraden, Winkel

Eine Strecke ist die kürzeste Verbindung zweier Punkte.

Die Schreibweise

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 981006045
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$[AB]\quad$ steht für die Strecke von A nach B.

Der Abstand von Anfangs- und Endpunkt ist die Länge der Strecke.

Mit der Schreibweise

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1006117262
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

${\overline {AB}}=5~cm\quad$ gibt man die Länge der Stecke an.

Verlängert man eine Strecke über einen Punkt bzw. über beide Punkte hinaus, so einsteht eine Halbgerade bzw. Gerade.

Beispiele:

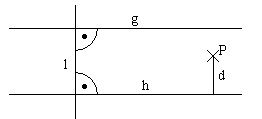
g ist parallel zu h:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008539928
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$g\|h$. g ist senkrecht zu l (g ist Lot zu l):

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 986870091
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$g\perp l$

Der Abstand d eines Punktes P von einer Geraden ist die Länge der senkrechten Verbindungsstrecke.

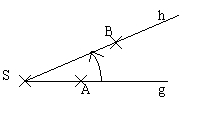
Zwei Halbgeraden mit demselben Anfangspunkt S teilen die Ebene in zwei Teile. Jeder Teil (mit Rand) heißt Winkel.

Bezeichnungen:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008539926
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\angle (g,h)$ oder

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1004092662
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\angle ASB$ oder kleine griechische Buchstaben:

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 990654508
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\alpha \$ alpha,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1004616599
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\beta \$ beta,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 998479342
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\gamma \$ gamma,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008539924
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\delta \$ delta,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 996585983
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\epsilon \$ epsilon,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 998417364
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\eta \$ eta, $\vartheta \$ theta,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 993542041
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\mu \$ my,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1004616605
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\sigma \$ sigma,

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 989940747
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$\tau \$ tau, $\varphi \$ phi, $\omega \$ omega

Winkelarten:

• Nullwinkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 981006049
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $\alpha =0^{o}$
• spitze Winkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 998417362
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $0^{o}<\alpha <90^{o}$
• rechter Winkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 986870093
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $\alpha =90^{o}$
• stumpfe Winkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 987524771
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $90^{o}<\alpha <180^{o}$
• gestreckter Winkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 987524769
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $\alpha =180^{o}$
• überstumpfe Winkel:
  

  Error

  Too many requests (f061ab2)

  If you report this error to the Wikimedia System Administrators, please include the details below.

  Request served via cp3066 cp3066, Varnish XID 1008539930
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


  Sensitive client information

  IP address: 188.64.62.105

  $180^{o}<\alpha <360^{o}$

GWM 5.13 Koordinatensystem

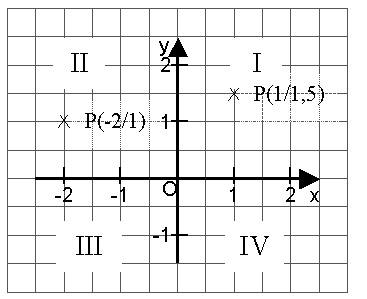
Ein Koordinatensystem besteht aus zwei senkrechten Zahlenstrahlen mit gemeinsamem Nullpunkt. Die x-Achse heißt auch Abszisse, die y-Achse auch Ordinate.

Ein Punkt P(x/y) ist durch seine Koordinaten festgelegt.

Die Ebene wird in vier Quadranten unterteilt.

GWM 5.14 Zählprinzip, Baumdiagramm

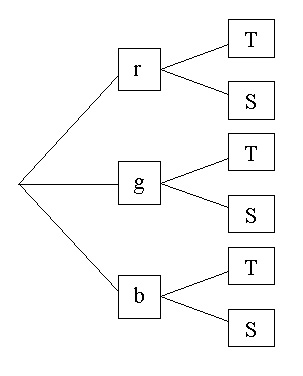
Veranschaulichung am Baumdiagramm:

Jeder Pfad durch den Baum steht für eine Kombinationsmöglichkeit.

Hat die erste Verzeigung

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 987656543
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$n\$ Äste und die zweite $m\$ Äste, so gibt es

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008670569
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$n\cdot m$ Möglichkeiten.

Beispiel:

Es gibt rote (r), grüne (g) und blaue (b) Schuluniformen. Sie sind als T-Shirt T oder Sweatshirt S erhältlich. Es gibt

Error

Too many requests (f061ab2)

If you report this error to the Wikimedia System Administrators, please include the details below.

Request served via cp3066 cp3066, Varnish XID 1008670571
Upstream caches: cp3066 int
Error: 429, Too many requests (f061ab2) at Mon, 12 Jan 2026 05:51:25 GMT


Sensitive client information

IP address: 188.64.62.105

$3\cdot 2=6$ Möglichkeiten, nämlich: rT, gT, bT, rS, gS, bS.

Web-Links

SMART-Aufgaben-Datenbank

---

Zurück zu Grundwissen Mathematik