SchulheftPh11: Unterschied zwischen den Versionen
Ba2282 (Diskussion | Beiträge) |
Ba2282 (Diskussion | Beiträge) |
||
| (50 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 96: | Zeile 96: | ||
===1.2 Das elektrische Feld=== | ===1.2 Das elektrische Feld=== | ||
| − | Die '''elektrische Feldstärke''' <math>\vec{E}</math> ist | + | Die '''elektrische Feldstärke''' <math>\vec{E}</math> (Einheit <math> 1~\frac{N}{C} = 1~\frac{V}{m} \ </math>) ist |
{| border="1" cellspacing="0" cellpadding="5" | {| border="1" cellspacing="0" cellpadding="5" | ||
| Zeile 121: | Zeile 121: | ||
|<math>E = \frac{U}{d}</math> | |<math>E = \frac{U}{d}</math> | ||
|} | |} | ||
| + | |||
[https://www.youtube.com/watch?v=2HhaQtvICe8 Millikan-Versuch Video Charge of an Electron: Millikan's Oil Drop Experiment von Tyler DeWitt] | [https://www.youtube.com/watch?v=2HhaQtvICe8 Millikan-Versuch Video Charge of an Electron: Millikan's Oil Drop Experiment von Tyler DeWitt] | ||
| Zeile 127: | Zeile 128: | ||
'''Potential und Äquipotentiallinien''' | '''Potential und Äquipotentiallinien''' | ||
| − | Das '''elektrische Potential''' <math>\varphi \ </math> eines Punktes im elektrischen Feld ist | + | Das '''elektrische Potential''' <math>\varphi \ </math> (Einheit <math> 1~V \ </math>) eines Punktes im elektrischen Feld ist |
{| border="1" cellspacing="0" cellpadding="5" | {| border="1" cellspacing="0" cellpadding="5" | ||
| Zeile 158: | Zeile 159: | ||
'''Kapazität eines Kondensators''' | '''Kapazität eines Kondensators''' | ||
| + | |||
| + | Die '''Kapazität''' <math>C \ </math> (Einheit "Farad", <math> 1~F = 1~\frac{As}{V} \ </math>) eines Kondensators ist definiert als | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>C = \frac{Q}{U} </math> | ||
| + | |} | ||
| + | |||
[https://phet.colorado.edu/sims/html/capacitor-lab-basics/latest/capacitor-lab-basics_de.html Kapazität Labor bei PhET] | [https://phet.colorado.edu/sims/html/capacitor-lab-basics/latest/capacitor-lab-basics_de.html Kapazität Labor bei PhET] | ||
[https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/versuche/kapazitaet-des-plattenkondensators Kapazität des Plattenkondensators bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/versuche/kapazitaet-des-plattenkondensators Kapazität des Plattenkondensators bei LeiFi-Physik] | ||
| + | |||
| + | Beim Plattenkondensator gilt: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>C = \epsilon_r \cdot \epsilon_0 \cdot \frac{A}{d} </math> | ||
| + | |} | ||
| + | |||
| + | mit der '''elektrischen Feldkonstante''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>\epsilon_0 = 8,8542\cdot 10^{-12}~\frac{As}{Vm} </math> | ||
| + | |} | ||
| + | |||
[https://www.leifiphysik.de/elektrizitaetslehre/kondensator-kapazitaet/ausblick/bauformen-von-kondensatoren Bauformen von Kondensatoren bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/kondensator-kapazitaet/ausblick/bauformen-von-kondensatoren Bauformen von Kondensatoren bei LeiFi-Physik] | ||
| Zeile 171: | Zeile 192: | ||
'''Schaltung von Kondensatoren''' | '''Schaltung von Kondensatoren''' | ||
| + | |||
| + | Parallelschaltung: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> C = C_1 + C_2 + ... + C_n \ </math> | ||
| + | |} | ||
| + | |||
| + | Reihenschaltung: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_n}</math> | ||
| + | |} | ||
[https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/aufgabe/quiz-zum-kondensator Quiz zum Kondensator bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/aufgabe/quiz-zum-kondensator Quiz zum Kondensator bei LeiFi-Physik] | ||
| + | |||
'''Energie im elektrischen Feld''' | '''Energie im elektrischen Feld''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>E_{el} = \frac{1}{2}\cdot Q \cdot U = \frac{1}{2}\cdot C \cdot U^2 </math> | ||
| + | |} | ||
[https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/kondensator-als-energiespeicher Kondensator als Energiespeicher bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/kondensator-als-energiespeicher Kondensator als Energiespeicher bei LeiFi-Physik] | ||
| Zeile 180: | Zeile 216: | ||
'''Coulombsches Gesetz''' | '''Coulombsches Gesetz''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> F = \frac{1}{4\pi\epsilon_{0}}\cdot \frac{|Q_1\cdot Q_2|}{r^2}</math> | ||
| + | |} | ||
[https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/coulomb-gesetz Gesetz von COULOMB bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/ladungen-felder-oberstufe/coulomb-gesetz Gesetz von COULOMB bei LeiFi-Physik] | ||
| + | |||
| + | [https://www.isb.bayern.de/download/22038/ph_2019_aalspdf.pdf Abitur 2019 Physik Bayern Ph 11-1] | ||
| + | |||
'''Elektrisches Feld und Potential von Punktladungen''' | '''Elektrisches Feld und Potential von Punktladungen''' | ||
| + | |||
| + | [[Datei:Elradialfeld.jpg|600px]] | ||
| + | |||
| + | Das elektrische Feld einer Punktladung ist ein '''Radialfeld''', es ist '''nicht homogen'''. | ||
| + | |||
| + | '''Elektrische Feldstärke eines Radialfeldes''' um die zentrale Punktladung <math>Q \ </math>: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>E = \frac{1}{4\pi \epsilon_0}\cdot \frac{Q}{r^2} </math> | ||
| + | |} | ||
| + | |||
| + | '''Potentialle Energie im Radialfeld''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>E_{pot} = Q_2\cdot E\cdot r = \frac{1}{4\pi \epsilon_0}\cdot \frac{Q\cdot Q_2}{r} </math> | ||
| + | |} | ||
| + | |||
| + | '''Elektrisches Potential im Radialfeld''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>\varphi = \frac{E_{pot}}{Q_2} = \frac{1}{4\pi \epsilon_0}\cdot \frac{Q}{r} </math> | ||
| + | |} | ||
| + | |||
[http://www.didaktikonline.physik.uni-muenchen.de/programme/e_feld/E_Feld.html Simulation elektrisches Feld und Potential von Prof. Dr. Raimund Girwidz LMU München] | [http://www.didaktikonline.physik.uni-muenchen.de/programme/e_feld/E_Feld.html Simulation elektrisches Feld und Potential von Prof. Dr. Raimund Girwidz LMU München] | ||
| Zeile 192: | Zeile 258: | ||
[https://www.isb.bayern.de/download/12838/abiturpruefung_physik_2013.pdf Abitur 2013 Physik Bayern Ph 11-1] | [https://www.isb.bayern.de/download/12838/abiturpruefung_physik_2013.pdf Abitur 2013 Physik Bayern Ph 11-1] | ||
| + | |||
==2. Statisches magnetisches Feld== | ==2. Statisches magnetisches Feld== | ||
| Zeile 202: | Zeile 269: | ||
[https://www.leifiphysik.de/elektrizitaetslehre/magnetisches-feld-spule/ausblick/erdmagnetfeld Erdmagnetfeld bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/magnetisches-feld-spule/ausblick/erdmagnetfeld Erdmagnetfeld bei LeiFi-Physik] | ||
| + | |||
| + | [https://www.ardmediathek.de/video/alpha-centauri/was-passiert-wenn-das-erdmagnetfeld-verschwindet/ard-alpha/Y3JpZDovL2JyLmRlL3ZpZGVvLzY0NTAzMTA4LTkwNjEtNGFlNC05Yzk2LWIzYjY1NGRmNDI3Yw/ Was passiert, wenn das Erdmagnetfeld verschwindet? Video alpha-centauri bei ardmediathek.de] | ||
| + | |||
| + | [https://www.leifiphysik.de/elektrizitaetslehre/magnetisches-feld-spule Magnetisches Feld - Spule bei LeiFi-Physik] | ||
| + | |||
'''Kraft auf stromdurchflossene Leiter im Magnetfeld''' | '''Kraft auf stromdurchflossene Leiter im Magnetfeld''' | ||
| Zeile 213: | Zeile 285: | ||
[https://de.m.wikipedia.org/wiki/Wasserstoffwirtschaft#Effizienz_der_Energiekette Effizienz der Energiekette Wasserstoff vs. Elektro bei Wikipedia.de] | [https://de.m.wikipedia.org/wiki/Wasserstoffwirtschaft#Effizienz_der_Energiekette Effizienz der Energiekette Wasserstoff vs. Elektro bei Wikipedia.de] | ||
| − | '''Die magnetische Flussdichte B''' | + | |
| + | '''Die magnetische Flussdichte B''' (Einheit "Tesla", <math> 1~T = 1~\frac{N}{Am} = 1~\frac{Vs}{m^2} \ </math>) | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>B = \frac{F}{I\cdot l} </math> | ||
| + | |} | ||
| + | |||
| + | Der Vektor der '''magnetischen Flussdichte''' <math>\vec{B} \ </math> kennzeichnet die Stärke des Magnetfelds und zeigt in Richtung der magnetischen Feldlinien. | ||
[https://www.leifiphysik.de/elektrizitaetslehre/kraft-auf-stromleiter-e-motor/versuche/kraftmessung-mit-der-stromwaage Stromwaage bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/kraft-auf-stromleiter-e-motor/versuche/kraftmessung-mit-der-stromwaage Stromwaage bei LeiFi-Physik] | ||
| Zeile 220: | Zeile 299: | ||
[https://www.tesla-info.de/index.htm Nikola Tesla - vergessenes Genie auf tesla-info.de] | [https://www.tesla-info.de/index.htm Nikola Tesla - vergessenes Genie auf tesla-info.de] | ||
| + | |||
'''Magnetische Flussdichte im Innern einer lang gestreckten Spule''' | '''Magnetische Flussdichte im Innern einer lang gestreckten Spule''' | ||
| + | |||
| + | [[Datei:VFPt cylindrical coil real.png]] | ||
[https://www.leifiphysik.de/elektrizitaetslehre/magnetisches-feld-spule/magnetfeld-einer-zylinderspule Magnetfeld einer Zylinderspule bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/magnetisches-feld-spule/magnetfeld-einer-zylinderspule Magnetfeld einer Zylinderspule bei LeiFi-Physik] | ||
| + | |||
| + | [https://www.leifiphysik.de/elektrizitaetslehre/stroeme-magnetisches-feld/versuche/magnetisches-feld-von-langen-zylinderspulen Magnetisches Feld von langen Zylinderspulen bei LeiFi-Physik] | ||
| + | |||
| + | Im Inneren einer lang gestreckten Spule ist die magnetische Flussdichte nahezu konstant, die Feldlinien verlaufen parallel zur Spulenachse, das Magnetfeld ist nahezu homogen und es gilt: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>B = \mu_r \cdot \mu_0 \cdot I \cdot \frac{N}{l} </math> | ||
| + | |} | ||
| + | |||
| + | mit der '''magnetischen Feldkonstante''' | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>\mu_0 = 4\pi\cdot 10^{-7}~\frac{Vs}{Am} </math> | ||
| + | |} | ||
| + | |||
'''Magnetfeld um einen geraden, stromdurchflossenen Leiter''' | '''Magnetfeld um einen geraden, stromdurchflossenen Leiter''' | ||
| + | |||
| + | [[Datei:VFPt wire out with-some-compass-needles.png]] | ||
[http://www.walter-fendt.de/html5/phde/magneticfieldwire_de.htm Magnetfeld eines geraden stromdurchflossenen Leiters von W. Fendt] | [http://www.walter-fendt.de/html5/phde/magneticfieldwire_de.htm Magnetfeld eines geraden stromdurchflossenen Leiters von W. Fendt] | ||
| + | |||
| + | Die magnetischen Feldlinien bilden konzentrische Kreise, die magnetische Flussdichte nimmt mit zunehmender Entfernung <math> r \ </math> vom Leiter proportional zu <math> \frac{1}{r} \ </math> ab und es gilt: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>B = \mu_0 \cdot \frac{I}{2\pi \cdot r} </math> | ||
| + | |} | ||
| + | |||
[https://www.leifiphysik.de/elektrizitaetslehre/kraft-auf-stromleiter-e-motor/ampere-definition Ampere Definition bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/kraft-auf-stromleiter-e-motor/ampere-definition Ampere Definition bei LeiFi-Physik] | ||
| + | |||
==3. Bewegung geladener Teilchen in Feldern== | ==3. Bewegung geladener Teilchen in Feldern== | ||
| Zeile 238: | Zeile 345: | ||
[http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/index.php Bewegung von Elektronen im E- und B-Feld LMU München] | [http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/index.php Bewegung von Elektronen im E- und B-Feld LMU München] | ||
| + | |||
===3.1 In homogenen elektrischen Feldern=== | ===3.1 In homogenen elektrischen Feldern=== | ||
| Zeile 243: | Zeile 351: | ||
'''Bewegung geladener Teilchen im homogenen Längsfeld''' | '''Bewegung geladener Teilchen im homogenen Längsfeld''' | ||
| − | [ | + | [https://virtuelle-experimente.de/kanone/klassisch/aufbau.php Elektronenkanone (Längsfeld) LMU München] |
| + | '''Beschleunigung''' eines geladenen Teilchens der Ladung <math>q \ </math> und der Masse <math>m \ </math> beim Durchlaufen der Spannung <math>U_B \ </math> auf dem Weg <math>d \ </math> im elektrischen Längsfeld: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>a = \frac{q\cdot U_B}{m \cdot d} </math> | ||
| + | |} | ||
| + | |||
| + | '''Endgeschwindigkeit''' dabei: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>v = \sqrt{2\cdot \frac{q}{m}\cdot U_B} </math> | ||
| + | |} | ||
| + | |||
| + | Für die '''kinetische Energie''' des geladenen Teilchens gilt also: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>E_{kin} = \frac{1}{2}\cdot m\cdot v^2 = q\cdot U_B </math> | ||
| + | |} | ||
| + | |||
| + | Dies führt zur Definition der Einheit '''Elektronenvolt''' (eV) als Energieeinheit in der Atom- und Kernphysik: | ||
| + | |||
| + | <math>1 eV \ </math> ist die Energie, die ein Ladungsträger mit <math>q = e \ </math> (Elementarladung) erhält, wenn er aus der Ruhe die Spannung <math>1 V \ </math> durchläuft. | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>1 eV = 1,602\cdot 10^{-19} J = 4,45\cdot 10^{-26} kWh </math> | ||
| + | |} | ||
| + | |||
| + | |||
'''Geladene Teilchen im homogenen Querfeld''' | '''Geladene Teilchen im homogenen Querfeld''' | ||
[https://www.leifiphysik.de/elektrizitaetslehre/bewegte-ladungen-feldern/ausblick/oszilloskop Oszilloskop bei LeiFi-Physik] | [https://www.leifiphysik.de/elektrizitaetslehre/bewegte-ladungen-feldern/ausblick/oszilloskop Oszilloskop bei LeiFi-Physik] | ||
| + | |||
| + | '''Beschleunigung''' eines geladenen Teilchens der Ladung <math>q \ </math> und der Masse <math>m \ </math> beim Durchlaufen eines homogenen elektrischen Querfelds (Ablenkkondensator) | ||
| + | |||
| + | mit der Spannung <math>U' \ </math> und dem Plattenabstand <math>d' \ </math>: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>a_y = \frac{q\cdot U'}{m \cdot d'} </math> | ||
| + | |} | ||
| + | |||
| + | Gleichung für die parabelförmige '''Flugbahn''' innerhalb des Ablenkkondensators: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>y(x) = \frac{1}{4}\cdot \frac{U'}{U_B}\cdot \frac{x^2}{d'} </math> | ||
| + | |} | ||
[http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/e-feld/hypothesen/Versuchsaufbau.php Elektronenablenkröhre (Querfeld) LMU München] | [http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/e-feld/hypothesen/Versuchsaufbau.php Elektronenablenkröhre (Querfeld) LMU München] | ||
===3.2 In homogenen magnetischen Feldern=== | ===3.2 In homogenen magnetischen Feldern=== | ||
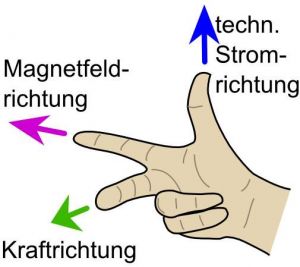
| + | [[Bild:Rechtehandregel.jpg|thumb|right|Drei-Finger-Regel der rechten Hand]] | ||
| + | |||
| + | Bewegen sich geladene Teilchen in einem Magnetfeld, so wirkt auf sie die '''Lorentzkraft'''. | ||
| + | |||
| + | Ist dabei die Magnetfeldrichtung senkrecht zum Stromfluss, so ergibt sich die Richtung der Lorentzkraft nach der "'''Drei-Finger-Regel der rechten Hand'''": | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |Daumen in technischer Stromrichtung (von + nach -) ('''U'''rsache) und | ||
| + | |||
| + | Zeigefinger in Magnetfeldrichtung (von Nord nach Süd) ('''V'''ermittlung) | ||
| + | |||
| + | ==> Mittelfinger zeigt in Richtung der Kraft ('''W'''irkung) | ||
| + | |} | ||
| + | |||
| + | Dann ist der '''Betrag der Lorentzkraft''' auf ein geladenen Teilchens der Ladung <math>q \ </math> mit der Geschwindigkeit <math>v \ </math> senkrecht zu einem Magnetfeld mit der magnetischen Flussdichte <math>B \ </math>: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>F_L = q\cdot v\cdot B \ </math> | ||
| + | |} | ||
| + | |||
'''Kreisbahn von Elektronen im Fadenstrahlrohr''' | '''Kreisbahn von Elektronen im Fadenstrahlrohr''' | ||
| + | |||
| + | In einer speziellen Röhre werden Elektronen in einem elektrischen Feld beschleunigt und in ein von Helmholtz-Spulen erzeugtes homogenes Magnetfeld gebracht und dort auf eine Kreisbahn mit Radius <math>r \ </math> abgelenkt. | ||
| + | |||
| + | Die Lorentzkraft <math>F_L \ </math> wirkt dabei als Zentripetalkraft <math>F_r \ </math>: | ||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>F_L = F_r \Longleftrightarrow q\cdot v\cdot B = m\cdot \frac{v^2}{r} \ </math> | ||
| + | |} | ||
[http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/b-feld/B-Feld/Helmholtzspulenpaar.php Elektronen im B-Feld (Kathodenstrahlröhre) LMU München] | [http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/b-feld/B-Feld/Helmholtzspulenpaar.php Elektronen im B-Feld (Kathodenstrahlröhre) LMU München] | ||
| + | |||
'''Spezifische Ladung / Masse von Elektronen''' | '''Spezifische Ladung / Masse von Elektronen''' | ||
| + | |||
| + | Der Quotient <math>\frac{e}{m_e} \ </math> wird als '''spezifische Ladung''' der Elektronen bezeichnet. | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>\frac{e}{m_e} = \frac{2\cdot U_B}{B^2\cdot r^2} \ </math> | ||
| + | |} | ||
| + | |||
| + | Einheitenbetrachtung dazu: <math>\frac{V}{T^2\cdot m^2} = \frac{V\cdot m^4}{V^2\cdot s^2\cdot m^2} = \frac{m^2}{V\cdot s^2} = \frac{kg\cdot m^2}{kg\cdot V\cdot s^2} = \frac{N\cdot m}{kg\cdot V} = \frac{VAs}{V\cdot kg} = \frac{As}{kg} \ </math> | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>\frac{e}{m_e} = 1,759\cdot 10^{11}~\frac{As}{kg} \ </math> | ||
| + | |} | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |<math>m_e = 9,109\cdot 10^{-31}~kg \ </math> | ||
| + | |} | ||
[http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/b-feld/e-m-bestimmung/historie.php e/m-Bestimmung LMU München] | [http://www.didaktik.physik.uni-muenchen.de/elektronenbahnen/b-feld/e-m-bestimmung/historie.php e/m-Bestimmung LMU München] | ||
| + | |||
'''Hall-Effekt''' | '''Hall-Effekt''' | ||
| Zeile 287: | Zeile 474: | ||
==4. Spezielle Relativitätstheorie== | ==4. Spezielle Relativitätstheorie== | ||
| − | Postulate | + | [https://www.youtube.com/watch?v=IXFf2mRxnkY Das Geheimnis der Zeit - Einsteins Relativitätstheorie] bei YouTube.com |
| + | |||
| + | [https://www.youtube.com/watch?v=8wb6LZtNs04 Das Relativitätsprinzip] bei Youtube.com | ||
| + | |||
| + | [https://www.youtube.com/watch?v=mt0vKjpAHfg Relativität in der SRT] bei YouTube.com | ||
| + | |||
| + | |||
| + | '''Postulate''' | ||
'''P1 Relativitätsprinzip''' | '''P1 Relativitätsprinzip''' | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | Die Naturgesetze gelten in allen gleichförmig zueinander bewegten Bezugssystemen in gleicher Weise. | ||
| + | |} | ||
'''P2 Konstanz der Lichtgeschwindigkeit''' | '''P2 Konstanz der Lichtgeschwindigkeit''' | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | Die Vakuumlichtgeschwindigkeit <math>c = 2,99792\cdot 10^8~\frac{m}{s} \ </math> ist unabhängig von der Bewegung der Lichtquelle und vom Bezugssystem, in dem sie gemessen wird, immer gleich groß. | ||
| + | |} | ||
| − | Folgerungen | + | |
| + | '''Folgerungen''' | ||
'''F1 Zeitdehnung''' | '''F1 Zeitdehnung''' | ||
| + | |||
| + | Bewegte Uhren gehen für einen äußeren Beobachter langsamer: <math>t = \frac{t'}{\sqrt{1-\frac{v^2}{c^2}}} \ </math> | ||
'''F2 Längenkontraktion''' | '''F2 Längenkontraktion''' | ||
| + | |||
| + | Körper erscheinen für einen äußeren Beobachter in Bewegungsrichtung verkürzt: <math>l = l' \cdot \sqrt{1-\frac{v^2}{c^2}} \ </math> | ||
'''F3 Relativität der Gleichzeitigkeit''' | '''F3 Relativität der Gleichzeitigkeit''' | ||
| + | |||
| + | Der Begriff "gleichzeitig" ist nicht absolut, sondern relativ, also abhängig vom Bezugssystem des Beobachters. | ||
'''F4 Raumzeit''' | '''F4 Raumzeit''' | ||
| + | |||
| + | Raum und Zeit stehen in direktem Zusammenhang und sind vom Bewegungszustand des Bezugssystems abhängig (vierdimensionale Raumzeit). | ||
| + | |||
| + | Um Raum zu überwinden, braucht man Zeit, aber die Lichtgeschwindigkeit ist das absolute Tempolimit! Raum lässt sich also nicht sofort überwinden, jeder Blick ist ein Blick in die Vergangenheit. | ||
'''F5 Massenzunahme''' | '''F5 Massenzunahme''' | ||
| + | |||
| + | Die Masse eines Körpers nimmt mit seiner Geschwindigkeit für einen äußeren Beobachter zu: <math>m = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \ </math> | ||
'''F6 Relativistische Energie / Äquivalenz von Masse und Energie''' | '''F6 Relativistische Energie / Äquivalenz von Masse und Energie''' | ||
| − | ==5. Elektromagnetische Induktion== | + | Die Gesamtenergie eines Körpers und seine dynamische Masse sind zueinander direkt proportional, Masse und Energie sind äquivalent: |
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>E = m \cdot c^2 \ </math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | [https://www.leifiphysik.de/relativitaetstheorie Relativitätstheorie] bei LeiFi-Physik | ||
| + | |||
| + | ==5. Elektromagnetische Induktion == | ||
| + | |||
| + | ==6. Elektromagnetische Schwingungen und Wellen == | ||
| + | |||
| + | [https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-schwingungen/versuche/elektromagnetischer-schwingkreis-simulation Elektromagnetischer Schwingkreis Simulation] bei LeiFi-Physik | ||
| + | |||
| + | |||
| + | [https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-wellen/versuche/dipolstrahlung-animation Dipolstrahlung Animation] bei LeiFi-Physik | ||
| − | |||
Aktuelle Version vom 11. Januar 2026, 18:55 Uhr
Physik GWPh7 GWPh8 GWPh9 GWPh10 SchulheftPh8 SchulheftPh9 SchulheftPh10 SchulheftPh12
Inhaltsverzeichnis
0. Wiederholung
(siehe Grundwissen Physik 10 oder LeiFi-Physik)
1. Statisches elektrisches Feld
1.1 Grundlagen der Elektrizitätslehre
Elektrische Ladung Q (Einheit "Coulomb", )
Einfaches Atommodell SchulheftPh9
Atomare Vorstellungen der Elektrizität bei LeiFi-Physik
Statische Elektrizität bei PhET
Leifi-Quiz Ladungseigenschaften
Ein Körper ist elektrisch negativ geladen, wenn auf ihm Elektronenüberschuss herrscht. Er ist positiv geladen, wenn auf ihm Elektronenmangel herrscht.
Die Elementarladung ist eine Naturkonstante - die kleinste frei vorkommende Ladung:
Influenz ist die Trennung von Ladungen eines Körpers unter dem Einfluss der von äußeren Ladungen ausgeübten elektrischen Kraft.
Elektrische Stromstärke I (Einheit "Ampere", )
Elektrischer Strom ist fließende Ladung.
Die elektrische Stromstärke gibt an, wie viel Ladung in der Zeit durch einen Leiterquerschnitt fließt:
Batterie-Widerstandsstromkreis bei PhET
Elektrische Grundgrößen bei LeiFi-Physik
Elektrische Spannung U (Einheit "Volt", )
Die elektrische Spannung ist die Ursache für den Stromfluss in einem Stromkreis.
Elektrische Spannung bei LeiFi-Physik
Elektrischer Widerstand R (Einheit "Ohm", )
Umso mehr Strom der Stromstärke bei einer bestimmten Spannung fließt, desto kleiner ist der elektrische Widerstand.
Der elektrische Widerstand gibt an, wie stark der Stromfluss in einem Stromkreis behindert wird:
Elektrischer Widerstand bei LeiFi-Physik
Elektrische Arbeit/Energie W (Einheit "Joule", )
Elektrische Energie ist die Fähigkeit des elektrischen Stroms Arbeit zu verrichten, Wärme abzugeben oder Licht zu erzeugen.
Elektrische Leistung P (Einheit "Watt", )
Die elektrische Leistung gibt an, wie viel Energie pro Zeiteinheit in andere Energiearten umgewandelt wird:
Elektrische Arbeit und Leistung bei LeiFi-Physik
1.2 Das elektrische Feld
Die elektrische Feldstärke (Einheit ) ist
Ladungen und Felder bei LeiFi-Physik
Elektrisches Feldhockey bei PhET
Elektrisches Feld 1 - Telekolleg bei Youtube
Elektrisches Feld 2 - Telekolleg bei Youtube
Spannung, Faradayscher Käfig - Telekolleg bei Youtube
Fotokopierer und Laserdrucker bei LeiFi-Physik
Homogenes elektrisches Feld eines Plattenkondensators
Millikan-Versuch Video Charge of an Electron: Millikan's Oil Drop Experiment von Tyler DeWitt
Potential und Äquipotentiallinien
Das elektrische Potential (Einheit ) eines Punktes im elektrischen Feld ist
Die elektrische Spannung zwischen zwei Punkten im elektrischen Feld entspricht der Potentialdifferenz dieser Punkte:
Linien gleichen Potentials nennt man Äquipotentiallinien. Sie stehen senkrecht zu den Feldlinien.
Simulation elektrisches Feld und Potential von Prof. Dr. Raimund Girwidz LMU München
Aufgaben zum elektrischen Feld bei LeiFi-Physik
Musterabitur 2011 Physik Bayern Ph 11-2 Lösungen dazu
Abitur 2011 Physik Bayern Ph 11-1
Abitur 2015 Physik Bayern Ph 11-1
Kapazität eines Kondensators
Die Kapazität (Einheit "Farad", ) eines Kondensators ist definiert als
Kapazität des Plattenkondensators bei LeiFi-Physik
Beim Plattenkondensator gilt:
mit der elektrischen Feldkonstante
Bauformen von Kondensatoren bei LeiFi-Physik
Auseinanderziehen eines Plattenkondensators bei LeiFi-Physik
Abitur 2011 Physik Bayern Ph 11-2
Schaltung von Kondensatoren
Parallelschaltung:
Reihenschaltung:
Quiz zum Kondensator bei LeiFi-Physik
Energie im elektrischen Feld
Kondensator als Energiespeicher bei LeiFi-Physik
Coulombsches Gesetz
Gesetz von COULOMB bei LeiFi-Physik
Abitur 2019 Physik Bayern Ph 11-1
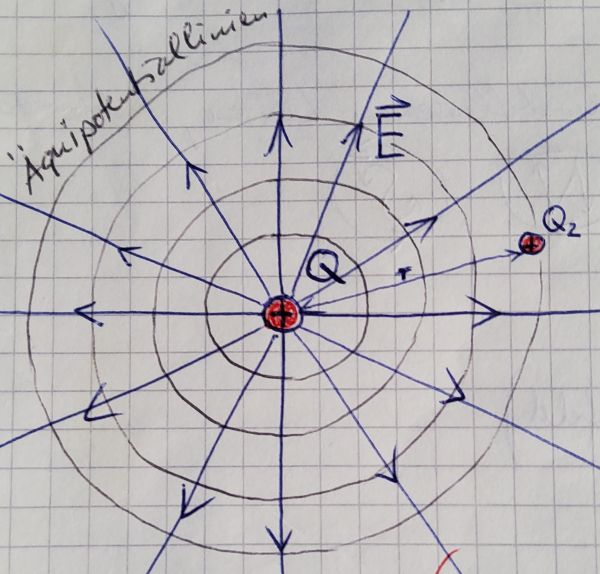
Elektrisches Feld und Potential von Punktladungen
Das elektrische Feld einer Punktladung ist ein Radialfeld, es ist nicht homogen.
Elektrische Feldstärke eines Radialfeldes um die zentrale Punktladung :
Potentialle Energie im Radialfeld
Elektrisches Potential im Radialfeld
Simulation elektrisches Feld und Potential von Prof. Dr. Raimund Girwidz LMU München
Überlagerung elektrischer Felder bei LeiFi-Physik
Abitur 2013 Physik Bayern Ph 11-1
2. Statisches magnetisches Feld
Permanentmagnetismus bei LeiFi-Physik
Felder Dauermagneten bei LeiFi-Physik
Erdmagnetfeld bei LeiFi-Physik
Was passiert, wenn das Erdmagnetfeld verschwindet? Video alpha-centauri bei ardmediathek.de
Magnetisches Feld - Spule bei LeiFi-Physik
Kraft auf stromdurchflossene Leiter im Magnetfeld
Kraft auf stromführende Leiter im Magnetfeld bei LeiFi-Physik
Elektromotor-Applet von Walter Fendt
Sendung mit der Maus - Wie funktioniert ein Elektromotor? bei YouTube.com
Effizienz der Energiekette Wasserstoff vs. Elektro bei Wikipedia.de
Die magnetische Flussdichte B (Einheit "Tesla", )
Der Vektor der magnetischen Flussdichte kennzeichnet die Stärke des Magnetfelds und zeigt in Richtung der magnetischen Feldlinien.
Nikola Tesla - Das vergessene Genie (Valeks Studios bei YouTube)
Nikola Tesla - vergessenes Genie auf tesla-info.de
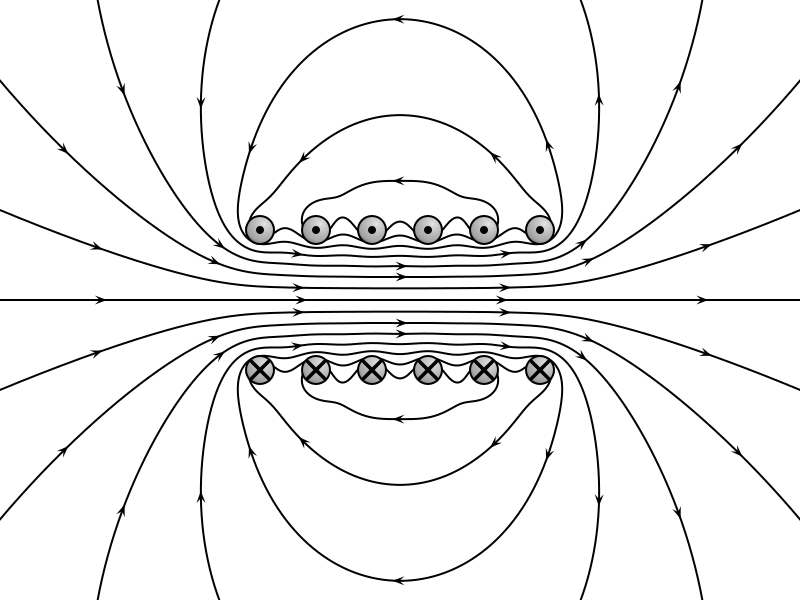
Magnetische Flussdichte im Innern einer lang gestreckten Spule
Magnetfeld einer Zylinderspule bei LeiFi-Physik
Magnetisches Feld von langen Zylinderspulen bei LeiFi-Physik
Im Inneren einer lang gestreckten Spule ist die magnetische Flussdichte nahezu konstant, die Feldlinien verlaufen parallel zur Spulenachse, das Magnetfeld ist nahezu homogen und es gilt:
mit der magnetischen Feldkonstante
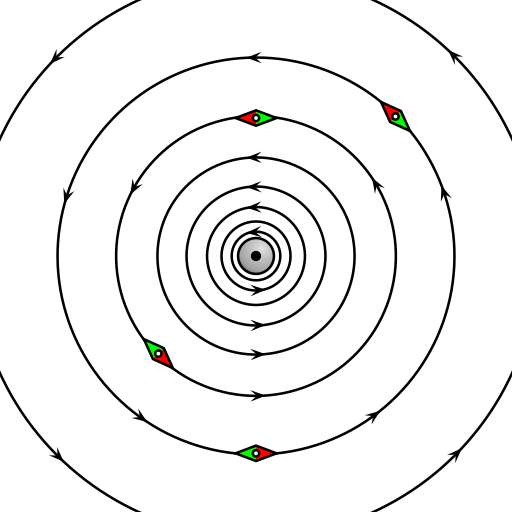
Magnetfeld um einen geraden, stromdurchflossenen Leiter
Magnetfeld eines geraden stromdurchflossenen Leiters von W. Fendt
Die magnetischen Feldlinien bilden konzentrische Kreise, die magnetische Flussdichte nimmt mit zunehmender Entfernung vom Leiter proportional zu ab und es gilt:
Ampere Definition bei LeiFi-Physik
3. Bewegung geladener Teilchen in Feldern
Glühelektrischer Effekt bei LeiFi-Physik
Bewegte Ladungen in Feldern bei LeiFi-Physik
Bewegung von Elektronen im E- und B-Feld LMU München
3.1 In homogenen elektrischen Feldern
Bewegung geladener Teilchen im homogenen Längsfeld
Elektronenkanone (Längsfeld) LMU München
Beschleunigung eines geladenen Teilchens der Ladung und der Masse beim Durchlaufen der Spannung auf dem Weg im elektrischen Längsfeld:
Endgeschwindigkeit dabei:
Für die kinetische Energie des geladenen Teilchens gilt also:
Dies führt zur Definition der Einheit Elektronenvolt (eV) als Energieeinheit in der Atom- und Kernphysik:
ist die Energie, die ein Ladungsträger mit (Elementarladung) erhält, wenn er aus der Ruhe die Spannung durchläuft.
Geladene Teilchen im homogenen Querfeld
Beschleunigung eines geladenen Teilchens der Ladung und der Masse beim Durchlaufen eines homogenen elektrischen Querfelds (Ablenkkondensator)
mit der Spannung und dem Plattenabstand :
Gleichung für die parabelförmige Flugbahn innerhalb des Ablenkkondensators:
Elektronenablenkröhre (Querfeld) LMU München
3.2 In homogenen magnetischen Feldern
Bewegen sich geladene Teilchen in einem Magnetfeld, so wirkt auf sie die Lorentzkraft.
Ist dabei die Magnetfeldrichtung senkrecht zum Stromfluss, so ergibt sich die Richtung der Lorentzkraft nach der "Drei-Finger-Regel der rechten Hand":
| Daumen in technischer Stromrichtung (von + nach -) (Ursache) und
Zeigefinger in Magnetfeldrichtung (von Nord nach Süd) (Vermittlung) ==> Mittelfinger zeigt in Richtung der Kraft (Wirkung) |
Dann ist der Betrag der Lorentzkraft auf ein geladenen Teilchens der Ladung mit der Geschwindigkeit senkrecht zu einem Magnetfeld mit der magnetischen Flussdichte :
Kreisbahn von Elektronen im Fadenstrahlrohr
In einer speziellen Röhre werden Elektronen in einem elektrischen Feld beschleunigt und in ein von Helmholtz-Spulen erzeugtes homogenes Magnetfeld gebracht und dort auf eine Kreisbahn mit Radius abgelenkt.
Die Lorentzkraft wirkt dabei als Zentripetalkraft :
Elektronen im B-Feld (Kathodenstrahlröhre) LMU München
Spezifische Ladung / Masse von Elektronen
Der Quotient wird als spezifische Ladung der Elektronen bezeichnet.
Einheitenbetrachtung dazu:
Hall-Effekt
Massenspektrograf / Geschwindigkeitsfilter
WIENsches Geschwindigkeitsfilter bei LeiFi-Physik
Massenspektrograf bei LeiFi-Physik
Abituraufgabe Zyklotron 2011 bei LeiFi-Physik
CERN Education Unterrichtsmaterialien Teilchenphysik
Versuche von Kaufmann und Bucherer
Versuch von Bucherer bei LeiFi-Physik
4. Spezielle Relativitätstheorie
Das Geheimnis der Zeit - Einsteins Relativitätstheorie bei YouTube.com
Das Relativitätsprinzip bei Youtube.com
Relativität in der SRT bei YouTube.com
Postulate
P1 Relativitätsprinzip
| Die Naturgesetze gelten in allen gleichförmig zueinander bewegten Bezugssystemen in gleicher Weise. |
P2 Konstanz der Lichtgeschwindigkeit
| Die Vakuumlichtgeschwindigkeit ist unabhängig von der Bewegung der Lichtquelle und vom Bezugssystem, in dem sie gemessen wird, immer gleich groß. |
Folgerungen
F1 Zeitdehnung
Bewegte Uhren gehen für einen äußeren Beobachter langsamer:
F2 Längenkontraktion
Körper erscheinen für einen äußeren Beobachter in Bewegungsrichtung verkürzt:
F3 Relativität der Gleichzeitigkeit
Der Begriff "gleichzeitig" ist nicht absolut, sondern relativ, also abhängig vom Bezugssystem des Beobachters.
F4 Raumzeit
Raum und Zeit stehen in direktem Zusammenhang und sind vom Bewegungszustand des Bezugssystems abhängig (vierdimensionale Raumzeit).
Um Raum zu überwinden, braucht man Zeit, aber die Lichtgeschwindigkeit ist das absolute Tempolimit! Raum lässt sich also nicht sofort überwinden, jeder Blick ist ein Blick in die Vergangenheit.
F5 Massenzunahme
Die Masse eines Körpers nimmt mit seiner Geschwindigkeit für einen äußeren Beobachter zu:
F6 Relativistische Energie / Äquivalenz von Masse und Energie
Die Gesamtenergie eines Körpers und seine dynamische Masse sind zueinander direkt proportional, Masse und Energie sind äquivalent:
Relativitätstheorie bei LeiFi-Physik
5. Elektromagnetische Induktion
6. Elektromagnetische Schwingungen und Wellen
Elektromagnetischer Schwingkreis Simulation bei LeiFi-Physik
Dipolstrahlung Animation bei LeiFi-Physik
Physik GWPh7 GWPh8 GWPh9 GWPh10 SchulheftPh8 SchulheftPh9 SchulheftPh10 SchulheftPh12