SchulheftPh9
Physik GWPh7 GWPh8 GWPh9 SchulheftPh8 SchulheftPh10 SchulheftPh11 SchulheftPh12
Inhaltsverzeichnis
- 1 0. Wiederholung
- 2 1. Elektrik
- 3 2. Atome
- 4 3. Kinematik und Dynamik geradliniger Bewegungen
0. Wiederholung
(siehe Grundwissen Physik 8 oder LeiFi-Physik)
1. Elektrik
1.1 Magnetisches und elektrisches Feld
Magnete und ihre Eigenschaften
Ein Magnet ist ein Körper, der die sogenannten ferromagnetischen Stoffe (Eisen, Nickel, Kobalt und einige bestimmte Legierungen) anzieht.
Jeder Magnet hat mindestens zwei magnetische Pole, den Nord- und Südpol. Dabei ist der Nordpol der Pol, der bei freier Aufhängung des Magneten nach Norden zeigt.
| Gleichnamige Magnetpole stoßen sich ab und ungleichnamige Magnetpole ziehen sich an! |
(siehe Permanentmagnetismus bei LeiFi-Physik)
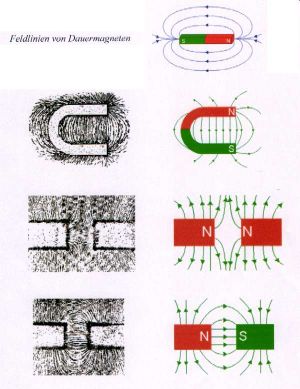
Jedes Magnetfeld lässt sich mithilfe eines Feldlinienbildes modellhaft veranschaulichen. Die Feldlinien verlaufen außerhalb des Magneten vom Nord- zum Südpol und schneiden sich nicht. Am Feldlinienbild kann man erkennen, in welcher Richtung Kräfte auf kleine Magnete im Magnetfeld wirken.
Magnetfelder stromdurchflossener Leiter
Um stromdurchflossene Leiter (auch um stromdurchflossene Spulen) existiert ein Magnetfeld.
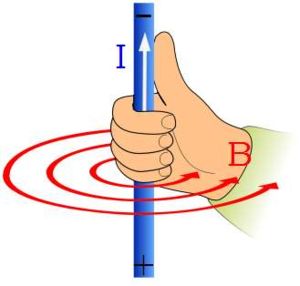
Der Zusammenhang zwischen technischer Stromrichtung und der Richtung des Magnetfeldes lässt sich mit der "Rechte-Faust-Regel" darstellen:
| Wenn der abgespreizte Daumen der rechten Hand in die technische Stromrichtung zeigt, so gibt die Richtung der anderen Finger die Richtung des Magnetfeldes an. |
(siehe Ströme und magnetisches Feld bei LeiFi-Physik)
Die Stärke des Magnetfelds einer stromdurchflossenen Spule kann man vergrößern, indem man
- die Stromstärke in der Spule erhöht,
- die Windungszahl der Spule größer wählt,
- eine kürzere Spule (mit gleicher Windungszahl) nimmt,
- einen Eisenkern in die Spule bringt.
Die Lorentzkraft
Auf einen stromdurchflossenen Leiter in einem Magnetfeld wirkt eine Kraft.
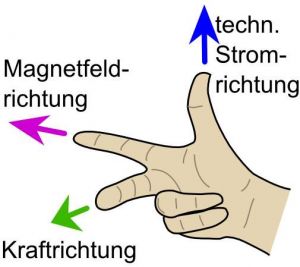
Ist dabei die Magnetfeldrichtung senkrecht zum Stromfluss, so ergibt sich die Richtung der Kraft nach der "Rechte-Hand-Regel":
| Daumen in technischer Stromrichtung (von + nach -) (Ursache) und
Zeigefinger in Magnetfeldrichtung (von Nord nach Süd) (Vermittlung) ==> Mittelfinger zeigt in Richtung der Kraft auf den Leiter (Wirkung) |
(siehe Kraft auf stromführende Leiter im Magnetfeld bei LeiFi-Physik)
Diese Erscheinung nennt man elektromotorisches Prinzip, welches z.B. bei elektrischen Messgeräten (Drehspulinstrument), bei Lautsprechern oder beim Elektromotor genutzt wird.
(siehe Elektromotor-Applet von Walter Fendt)
Man nennt die Kraft, die auf bewegte Ladungsträger in einem Magnetfeld wirkt, die Lorentzkraft.
(siehe Lorentzkraft bei LeiFi-Physik)
So wird z.B. der Elektronenstrahl in einer Fernsehbildröhre mit dem Magnetfeld stromdurchflossener Spulen abgelenkt.
(siehe Röhrenfernseher bei LeiFi-Physik)
Elektrische Ladung
Die Ladung eines Elektrons (negativ) und die Ladung eines Protons (positiv) ist die kleinste frei vorkommende Ladung - die sogenannte Elementarladung:
Ein Atom mit genauso viel Elektronen in der Atomhülle wie Protonen im Atomkern ist also elektrisch neutral.
Körper mit Elektronenüberschuss sind negativ geladen, während bei einem positiv geladenen Körper Elektronenmangel herrscht.
Die elektrische Ladung Q eines Körpers wird in der Einheit C ("Coulomb") angegeben.
| Gleichnamige Ladungen stoßen sich ab und ungleichnamige Ladungen ziehen sich an! |
(siehe Ballons und statische Elektrizität bei PhET)
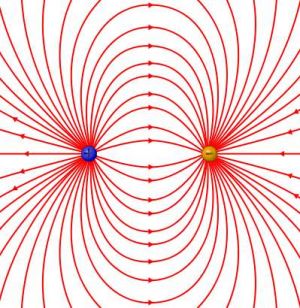
Das elektrische Feld
Im Raum um einen elektrisch geladenen Körper existiert ein elektrisches Feld. Es lässt sich mithilfe eines Feldlinienbildes modellhaft veranschaulichen. Die elektrischen Feldlinien verlaufen vom positiv geladenen Körper zum negativ geladenen Körper, schneiden sich nicht und stehen immer senkrecht zur Leiteroberfläche. Am Feldlinienbild kann man erkennen, in welcher Richtung Kräfte auf kleine positiv geladene Teilchen im elektrischen Feld wirken.
(siehe Elektrisches Feld - Feldlinien bei LeiFi-Physik)
Auf elektrisch geladene Teilchen wirkt in einem elektrischen Feld eine Kraft, sie werden also beschleunigt bzw. gebremst (Anwendung bei Elektronenstrahlröhre bzw. Oszilloskop).
(siehe Bewegte Ladungen in Feldern bei LeiFi-Physik)
1.2 Elektromagnetische Induktion
Wie kann elektrische Energie (Strom) erzeugt werden? Eine Antwort gibt das
Induktionsgesetz (nach Michael Faraday)
| Ändert sich das Magnetfeld, das eine Leiterschleife (bzw. Spule) umfasst, so wird in dieser eine Spannung induziert.
Diese Induktionsspannung ist umso größer,
|
(siehe Elektromagnetische Induktion bei LeiFi-Physik oder siehe Elektromagnetische Induktion und Faradays Elektromagnetisches Labor bei PhET)
Richtung des Induktionsstroms (Regel von Lenz)
| Der Induktionsstrom ist immer so gerichtet, dass er seiner Ursache entgegenwirkt. |
(siehe Lenzsche Regel bei LeiFi-Physik oder Lenz's Law by Michael W. Davidson and The Florida State University)
Wechselstromgenerator
(siehe Generator-Applet von Walter Fendt)
Eine Anordnung, bei der sich eine Spule in einem Magnetfeld dreht, wobei an der Spule eine Induktionsspannung abgegriffen wird, heißt Generator. Wechselt dabei die Polung der Spannung ständig, spricht man vom Wechselstromgenerator. In diesem rotiert eine Spule (Leiterschleife) gleichförmig in einem homogenen Magnetfeld, so dass eine sinusförmige Wechselspannung entsteht.
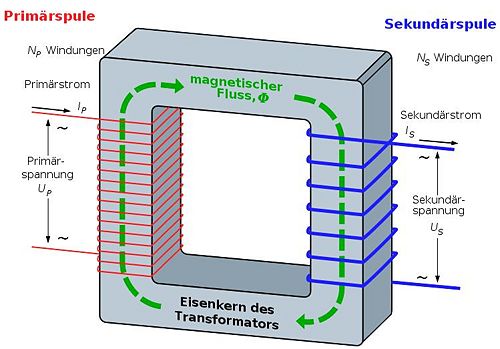
Transformator
Aufbau und Erklärung
Fließt ein Wechselstrom durch die Primärspule, so ändert sich mit der Frequenz des Wechselstroms auch das Magnetfeld durch die beiden Spulen. Daher wird in der Sekundärspule die Wechselspannung induziert.
Spannungen am Transformator
Für die Spannungen am (unbelasteten) Transformator gilt:
Mit einem Transformator lassen sich durch geeignete Wahl des Übersetzungsverhältnisses beliebig kleinere oder größere Wechselspannungen herstellen.
Stromübersetzung des Transformators
Im Idealfall () gilt für die Stromübersetzung:
Je größer die Stromübersetzung, desto kleiner die Spannungsübersetzung und umgekehrt!
Wirkungsgrad eines belasteten Transformators
(siehe Transformator bei LeiFi-Physik)
2. Atome
2.1 Aufbau der Atome
10 Hoch Reise durch den Mikro- und Makrokosmos mit Harald Lesch bei youtube.com
Alle Stoffe bestehen aus Atomen. Es gibt etwa 115 Elemente (Atomarten), aus denen die Stoffe auf unserer Welt aufgebaut sind.
Der Radius von Atomen liegt in einer Größenordnung von oder . Die Masse eines Atoms liegt bei etwa (je nach Element).
(siehe Ölfleckversuch - Aufbau und Durchführung - einfach und anschaulich erklärt bei YouTube.com und Ölfleckversuch bei LeiFi-Physik)
Modellvorstellung eines Atoms
Terra X - Rutherfordsche Streuversuch und Bohrsches Atommodell bei YouTube.com
Rutherfordscher Streuversuch bei YouTube.com
Discovery of the Nucleus: Rutherfords Gold Foil Experiment bei YouTube.com
Aus dem Streuversuch von Ernest Rutherford ergaben sich folgende Schlussfolgerungen und das Rutherfordsche Atommodell:
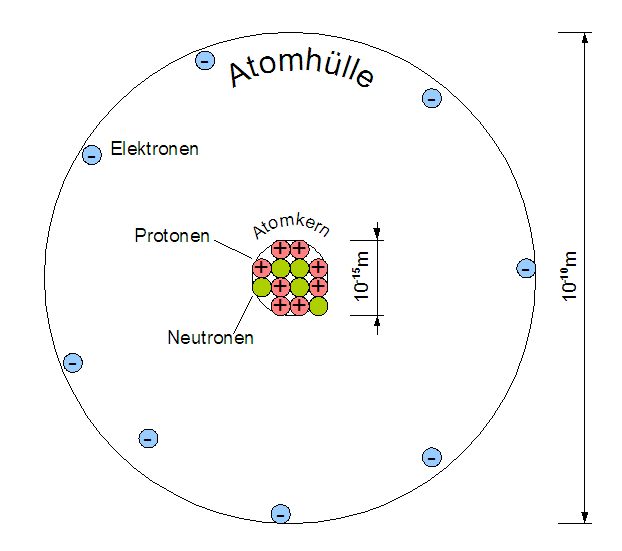
Fast die ganze Masse (ca. 99,99 %) des Atoms ist auf kleinsten Raum im Atomkern konzentriert. Der Atomkern ist im Vergleich zur Atomhülle winzig klein! Der Radius von Atomkernen beträgt etwa bis .
Die Atomhülle besteht aus negativ geladenen Elektronen, deren Masse nur etwa 1/1800 der Protonenmasse beträgt.
Der Atomkern besteht aus positiv geladenen Protonen und ungeladenen Neutronen. Diese Kernbausteine werden auch Nukleonen genannt, ihre Massen sind etwa gleich groß.
(siehe Atomaufbau und Streuversuch von Ernest Rutherford bei LeiFi-Physik und Rutherford Streuug bei PhET)
Der Atomkern - Chemie Endlich Verstehen bei YouTube.com
Periodentafel der Elemente bei LeiFi-Physik
Periodensystem der Elemente bei seilnacht.com
Die Anzahl der Nukleonen in einem Atomkern wird als Massenzahl bezeichnet, da man mit ihr die Atommasse näherungsweise bestimmen kann:
| Masse Atom = |
Die Massenzahl ergibt sich aus der Protonenzahl und der Neutronenzahl des Atomkerns eines bestimmten chemischen Elements. wird auch Kernladungszahl oder Ordnungszahl genannt und ist für alle Atome dieses Elements gleich. Die Anzahl der Neutronen kann dagegen unterschiedlich sein, was zu den sogenannten verschiedenen Isotopen dieses chemischen Elements führt.
Es gilt:
Symbolische Schreibweise für Atomkerne:
zum Beispiel:
Die Atomkernsorten nennt man auch Nuklide, die in einer Nuklidkarte zusammenfassend aufgelistet werden.
(siehe Nuklidkarte stabiler Kerne bei LeiFi-Physik Vollständige Nuklidkarte bei periodensystem-online.de)
Nuklide mit gleicher Protonenzahl aber verschiedener Massenzahl nennt man Isotope (z.B. Uran-Isotope )
Nuklidkarte Download "Nukliddaten" Freeware-Programm nur geeignet für Windows von Holger Werner
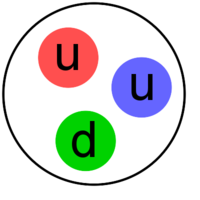
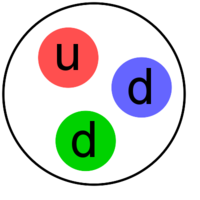
Protonen und Neutronen sind aus Quarks (Größenordnung ) zusammengesetzt:
u: up-Quark ( Ladung ), d: down-Quark ( Ladung ).
2.2 Aufnahme und Abgabe von Energie in der Atomhülle
Atommodell nach Niels Bohr (Schalenmodell) von musstewissen Chemie bei YouTube.com
Spektren und Beschreibungsarten des Lichts von Carl Schäfer bei YouTube.com
Emission und Absorption von Licht von Carl Schäfer bei YouTube.com
Neonlicht und andere Entladungslampen bei PhET
Schwarze Linien im Licht? Was sie verraten! mit Harald Lesch bei YouTube.com
Jeder Stoff sendet ein für ihn charakteristisches Spektrum aus. Die Ursache dafür sind für diesen Stoff typische Energieniveaus der Elektronen der Atomhülle, zwischen welchen diese wechseln können und dabei Licht einer bestimmten Wellenlänge aussenden oder absorbieren.
(siehe Atomarer Energieaustausch bei LeiFi-Physik)
Die Energieportionen, die bei diesen Übergängen in Form von Licht absorbiert oder emittiert werden, nennt man Lichtquanten oder Photonen.
Die Energie der Photonen liegt hier im Bereich einiger Elektronenvolt (eV).
Es gilt: .
Sichtbares Licht hat eine Energie zwischen etwa 1,5 eV (rotes Licht) und 3,3 eV (violettes Licht). Liegt die Energie der Photonen darunter, handelt es sich um unsichtbares infrarotes Licht, liegt sie darüber um unsichtbares ultraviolettes Licht.
(siehe auch Quiz zu Licht und Atom bei LeiFi-Physik)
Röntgenstrahlen
Röntgenstrahlung von Karlheinz Meier bei YouTube.com
Was ist Röntgenstrahlung? von GRS Deutschland bei YouTube.com
RÖNTGENSTRAHLUNG ganz einfach erklärt! von Der Physiklehrer bei YouTube.com
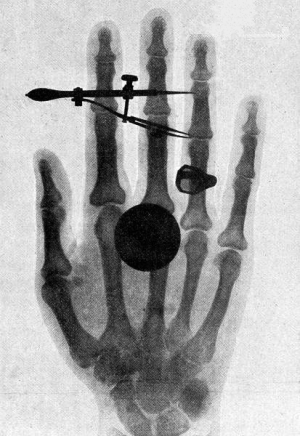
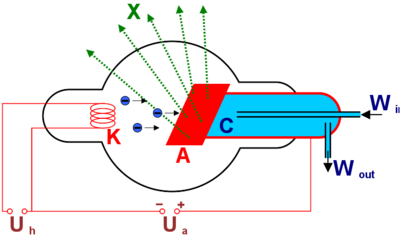
Treffen schnelle Elektronen auf eine Metallanode, so entstehen Röntgenstrahlen (nach W.C.Röntgen, 1895), deren Energie viel größer ist als die des sichtbaren Lichts (Energie der Röntgenstrahlung liegt zwischen 10 keV und 1 MeV, die zugehörige Wellenlänge liegt zwischen 1 nm und 10 pm). Deswegen können sie Materie durchdringen, Stoffe ionisieren, Zellen schädigen, Fluoreszenz erzeugen oder einen Film schwärzen.
(K: Glühkathode, A: Metallanode, C: Kühlung, X: Röntgenstrahlen, Ua: Beschleunigungsspannung, Uh: Heizspannung)
(siehe Erzeugung von Röntgenstrahlung bei LeiFi-Physik)
Man unterscheidet bei Röntgenstrahlen die sogenannte Bremsstrahlung (Elektronen werden im Anodenmaterial abgelenkt und abgebremst und dabei werden Photonen emittiert) und die charakteristische Strahlung (Inneres Hüllenelektron wird herausgeschlagen und beim Zurückfallen der Elektronen äußerer Schalen werden Photonen emittiert).
(siehe Bremsstrahlung und Charakteristische Röntgenstrahlung bei LeiFi-Physik)
Den Begriff "Röntgen" (oder auch: Radiographie) verwendet man mittlerweile für ein weitverbreitetes medizinisches Verfahren zur bildlichen Darstellung von Körperstrukturen wie Knochen, Gefäße und innere Organe. Seit Entdeckung der Röntgenstrahlen wurde es permanent weiterentwickelt und wird nach wie vor in nahezu allen Bereichen der Medizin genutzt (siehe auch Röntgen-Computertomographie bei LeiFi-Physik).
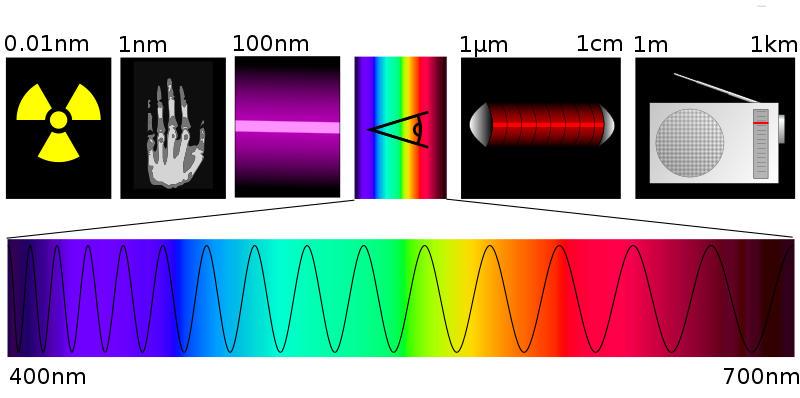
Illustration des gesamten Spektrums der elektromagnetischen Wellen:
2.3 Strahlung radioaktiver Nuklide
Was ist eigentlich Radioaktivität? von GRS Deutschland bei YouTube.com
Radioaktivität im Alltag von Welt der Wunder bei YouTube.com
(siehe auch Radioaktive Strahlung im Alltag bei quarks.de)
Tschernobyl - Die nukleare Katastrophe von MrWissen2go Geschichte bei YouTube.com
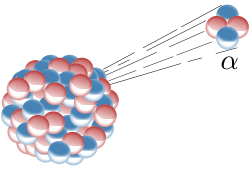
Radionuklide (radioaktive Nuklide) wandeln sich spontan (d.h. ohne äußere Anregung) unter Aussendung von -, - oder -Strahlung in andere Nuklide um. Diese radioaktive Strahlung besitzt eine sehr hohe Energie (einige MeV) und ist somit auch sehr gefährlich.
(siehe Radioaktivität - Einführung bei LeiFi-Physik)
Arten radioaktiver Strahlung
| -Strahlung | -Strahlung | -Strahlung | |
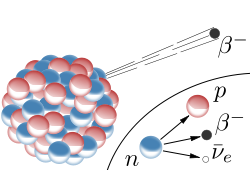
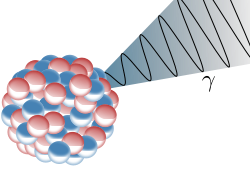
| Strahlung | Zweifach positiv geladene Heliumkerne (-Teilchen) | Elektronen (-Strahlung) oder Positronen (-Strahlung) | Energiereiche elektromagnetische Strahlung |
| Reaktion | () () |
||
| In der Nuklidkarte |
diagonal zwei nach links unten | diagonal eins nach links oben () diagonal eins nach rechts unten () |
- |
| Geschwindig- keit |
bis 10 % der Lichtgeschwindigkeit | bis 99 % der Lichtgeschwindigkeit | Lichtgeschwindigkeit 300000 km/s |
| Reichweite in Luft |
einige Zentimeter | einige Meter | viele Meter |
| Abschirmung | Blatt Papier | Aluminiumplatte | dicke Bleiplatte |
| Vorgang im Kern |
Kern stößt -Teilchen aus | Neutron --> Elektron und Proton () Proton --> Positron und Neutron () |
Änderung des Energiezustandes |
| Ablenkung im Magnetfeld |
ja, da positiv geladen | ja, da negativ geladen () ja, da positiv geladen () |
nein |
| Ablenkung im elektr. Feld |
ja, zur negativen Platte | ja, zur positiven Platte () ja, zur negativen Platte () |
nein |
(siehe Quiz zur radioaktiven Strahlung bei LeiFi-Physik)
Der Nachweis von radioaktiver Strahlung erfolgt durch Geiger-Müller-Zählrohre oder Nebelkammern(beides beruht auf ionisierender Wirkung) oder durch fotographische Schichten (Filme werden geschwärzt).
(siehe Geiger-Müller-Zählrohr bei LeiFi-Physik)
Halbwertszeit und Zerfallsgesetz
Die Zeitspanne, in welcher sich die Hälfte der anfangs vorhandenen radioaktiven Atomkerne eines bestimmten Nuklids umwandeln, wird Halbwertszeit genannt.
Zerfallsgesetz:
wobei : Anzahl der ursprünglich vorhandenen Atomkerne des Nuklids und : Anzahl der zur Zeit noch vorhandenen Atomkerne des Nuklids.
(siehe Halbwertszeit bei LeiFi-Physik oder Zerfallsgesetz-Applet von Walter Fendt)
Biologische Wirkung der radioaktiven Strahlung
Je größer die Energieaufnahme pro Körpermasse, desto größer ist auch die biologische Wirkung der auf den Körper treffenden Strahlung.
Energiedosis:
wobei die absorbierte Energie und die Masse des bestrahlten Körpers ist.
Die Einheit der Energiedosis ist: ("Gray")
Äquivalentdosis:
wobei der Bewertungsfaktor der jeweiligen Strahlung und die Energiedosis des bestrahlten Körpers ist.
Die Einheit der Äquivalentdosis ist: ("Sievert")
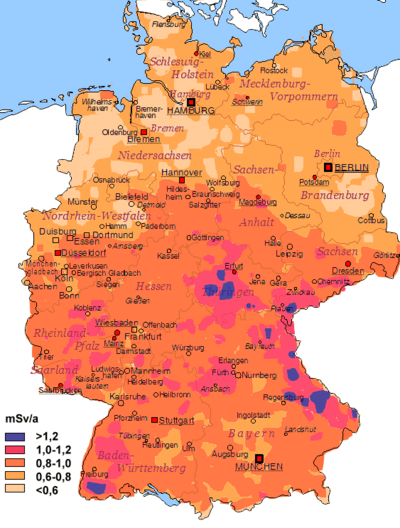
Die Äquivalentdosis wird zur Angabe der Strahlenbelastung verwendet.
(siehe Radioaktivität Einführung - Ausblicke bei LeiFi-Physik)
Strahlenschutz
| Abstand, Abschirmung, kurzzeitig und nicht in den Körper aufnehmen! |
(siehe Strahlenschutz bei LeiFi-Physik)
BG ETEM - Strahlungsarten, Aktivität, Halbwertszeit mit Prof. Harald Lesch von PanFilms Wolfes bei Youtube.com
BG ETEM - Strahlenwirkung mit Prof. Harald Lesch von PanFilms Wolfes bei Youtube.com
2.4 Kernumwandlungen und Anwendungen
Was passiert eigentlich bei Kernspaltung und Kernfusion? von GRS Deutschland bei Youtube.com
Kernspaltung
Schwere Atomkerne (Massenzahl >> 56) werden mit langsamen Neutronen beschossen. Dabei können sich diese Atomkerne in zwei Trümmerkerne und freiwerdende Neutronen spalten. Zusätzlich wird bei diesem Vorgang Energie frei, die z.B. in Kernkraftwerken genutzt wird.
Mögliche Zerfallsgleichungen:
Treffen diese freiwerdenden Neutronen (nach Abbremsung) wieder auf spaltbare Atomkerne, so kann es letztlich zu einer Kettenreaktion von Kernspaltungsprozessen kommen, bei der ungeheuere Mengen an Energie in kürzester Zeit frei werden.
WDR total phänomenal - Kernkraft Funktionsweise
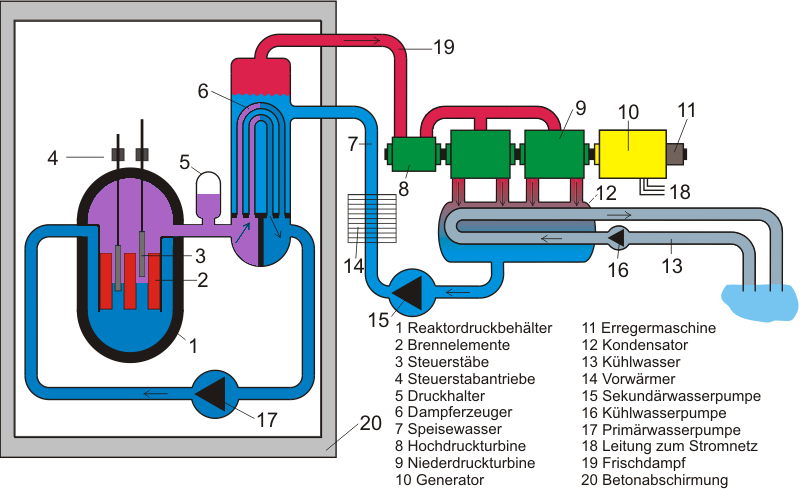
Aufbau eines Kernkraftwerks mit Druckwasserreaktor:
(siehe Kernspaltung bei LeiFi-Physik)
Kernfusion
Auch durch Verschmelzung besonders leichter Atomkerne zu schweren Kernen wird sehr viel Energie frei. Dieser Vorgang wird Kernfusion genannt und läuft nur bei extrem hohen Temperaturen (> 20 Mill. °C) und extremen Druck (> 10^15 Pa) ab.
Mögliche Fusionsreaktionen:
Königsweg Kernfusion? - Futuremag von ARTE bei Youtube.com
(siehe Kernfusion bei LeiFi-Physik)
Energien bei Kernumwandlungen
Die Nukleonen im Atomkern werden durch sehr starke Kernkräfte mit geringer Reichweite zusammengehalten. Diese Kernkräfte sind also deutlich stärker als die elektrischen Abstoßungskräfte zwischen Nukleonen.
Die Masse eines Atomkerns ist immer kleiner als die Masse seiner Bestandteile (Summe der Nukleonenmassen). Diese Differenz wird Massendefekt genannt, dem nach A. Einsteins spezieller Relativitätstheorie eine Energie entspricht. Diese Energie ist die Kernbindungsenergie, welche benötigt würde, um den Atomkern wieder in seine Bestandteile zu zerlegen.
(siehe Kernkraft (Animation) und Masse-Energie-Beziehung bei LeiFi-Physik)
3. Kinematik und Dynamik geradliniger Bewegungen
(Kinematik = Bewegungslehre gleichförmiger Bewegungen; Dynamik = Bewegungslehre beschleunigter Bewegungen)
3.1 Bewegungsabläufe in Diagrammen
| Gleichförmige Bewegung | Beschleunigte Bewegung |
| (z.B. Paket auf Förderband) | (z.B. anfahrendes Auto) |
| Geschwindigkeit: | Momentangeschwindigkeit, die sich laufend ändert |
| keine Beschleunigung: | Beschleunigung: |
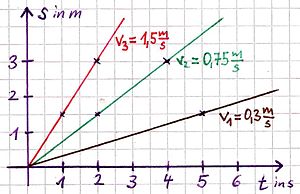
| Zeit-Ort-Diagramm:
Geraden mit der Geschwindigkeit als Steigung |
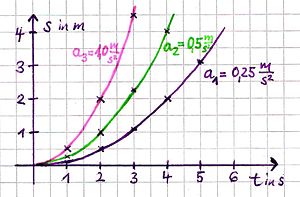
Zeit-Ort-Diagramm:
Teile von Parabeln mit der Geschwindigkeit als Steigung |
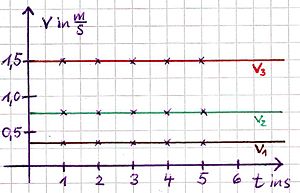
| Zeit-Geschwindigkeit-Diagramm:
Geraden parallel zur Zeitachse |
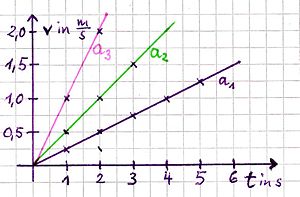
Zeit-Geschwindigkeit-Diagramm:
Geraden mit der Beschleunigung als Steigung |
(siehe Zeit-Ort-Diagramm, Zeit-Geschwindigkeits-Diagramm und Lineare Bewegung bei LeiFi-Physik)
3.2 Darstellung von Bewegungsabläufen mithilfe von Gleichungen
- Für eine gleichmäßig beschleunigte Bewegung eines Körpers aus der Ruhe gelten folgende Bewegungsfunktionen:
Dabei ist s(t) die zurückgelegte Strecke zum Zeitpunkt t, v(t) die Geschwindigkeit zum Zeitpunkt t und a(t) die Beschleunigung zum Zeitpunkt t.
Eliminiert man aus den ersten beiden Gleichungen die Zeit t, so erhält man eine weitere sehr gebräuchliche Beziehung zwischen Strecke, Geschwindigkeit und Beschleunigung:
(siehe Gleichmäßig beschleunigte Bewegungen bei LeiFi-Physik)
- Grundgesetz der Mechanik (Newton):
Wirkt auf einen Körper der Masse die Kraft , so wird er mit der Beschleunigung bewegt.
Die Kraft wird also so festgelegt, dass gilt:
Für die Einheiten gilt also:
oder anders:
(siehe Kraft und Bewegungsänderung bei LeiFi-Physik)
Physik GWPh7 GWPh8 GWPh9 SchulheftPh8 SchulheftPh10 SchulheftPh11 SchulheftPh12