SchulheftPh10: Unterschied zwischen den Versionen
Ba2282 (Diskussion | Beiträge) |
Ba2282 (Diskussion | Beiträge) |
||
| (115 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 158: | Zeile 158: | ||
Die Summe aller Kräfte auf einen Körper bestimmt, ob und wie er sich bewegt. | Die Summe aller Kräfte auf einen Körper bestimmt, ob und wie er sich bewegt. | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/kraefteaddition-und-zerlegung/versuche/schiefe-ebene-simulation Schiefe Ebene Simulation] bei LeiFi-Physik | ||
====Zusammensetzung von Kräften==== | ====Zusammensetzung von Kräften==== | ||
| − | (siehe [https://www.leifiphysik.de/mechanik/kraefteaddition-und-zerlegung Kräfteaddition | + | [[Datei:800px-Max und Moritz (Busch) 007.png|600px]] |
| + | |||
| + | (siehe [https://www.leifiphysik.de/mechanik/kraefteaddition-und-zerlegung/grundwissen/kraefteaddition Kräfteaddition] bei Leifiphysik) | ||
Ist die Summe aller Kräfte (=Gesamtkraft) auf einen Körper gleich null, so befindet er sich im '''Kräftegleichgewicht'''. | Ist die Summe aller Kräfte (=Gesamtkraft) auf einen Körper gleich null, so befindet er sich im '''Kräftegleichgewicht'''. | ||
| Zeile 167: | Zeile 171: | ||
====Zerlegung von Kräften==== | ====Zerlegung von Kräften==== | ||
| − | (siehe [https://www.leifiphysik.de/mechanik/kraefteaddition-und-zerlegung] bei Leifiphysik) | + | (siehe [https://www.leifiphysik.de/mechanik/kraefteaddition-und-zerlegung/grundwissen/zerlegung-einer-kraft-zwei-komponenten Kräftezerlegung] bei Leifiphysik) |
| + | |||
| + | [https://www.youtube.com/watch?v=aoxUyQq9Z34 Kräfte am Keil einfach erklärt] von Educational-Animation.com bei YouTube.com | ||
====Trägheitssatz von Newton (Newton I)==== | ====Trägheitssatz von Newton (Newton I)==== | ||
| + | [[Datei:Inertia demonstration applesauce.gif]] | ||
{| border="1" cellspacing="0" cellpadding="10" | {| border="1" cellspacing="0" cellpadding="10" | ||
| Zeile 175: | Zeile 182: | ||
|} | |} | ||
| + | (siehe [https://www.leifiphysik.de/mechanik/kraft-und-bewegungsaenderung/grundwissen/1-newtonsches-gesetz-traegheitsgesetz Trägheitsgesetz von Newton] bei Leifiphysik) | ||
| + | |||
| + | Video [https://www.youtube.com/watch?v=YR4rxhqj0g4 Tischdecke wegziehen - ohne Scherben] von Planet Schule bei YouTube.com | ||
====Grundgesetz der Mechanik (Newton II)==== | ====Grundgesetz der Mechanik (Newton II)==== | ||
| Zeile 183: | Zeile 193: | ||
Auf einen Körper der Masse m, der die Beschleunigung a erfährt, wirkt die Kraft F. | Auf einen Körper der Masse m, der die Beschleunigung a erfährt, wirkt die Kraft F. | ||
| + | |||
| + | (siehe [https://www.leifiphysik.de/mechanik/kraft-und-bewegungsaenderung/grundwissen/2-newtonsches-gesetz-aktionsprinzip 2. Newtonsches Gesetz] bei LeiFi-Physik) | ||
| Zeile 197: | Zeile 209: | ||
====Wechselwirkungsgesetz (Newton III)==== | ====Wechselwirkungsgesetz (Newton III)==== | ||
| + | [[Datei:Newton3.png|300px|right]] | ||
| − | Eine Kraft, die auf einen Körper wirkt, geht immer von anderen Körpern aus. | + | ''Siehe auch [https://www.leifiphysik.de/mechanik/kraft-und-bewegungsaenderung Kraft und Bewegungsänderung] bei LeiFi-Physik'' |
| + | |||
| + | '''Eine Kraft, die auf einen Körper wirkt, geht immer von anderen Körpern aus.''' | ||
{| border="1" cellspacing="0" cellpadding="10" | {| border="1" cellspacing="0" cellpadding="10" | ||
| Zeile 208: | Zeile 223: | ||
Vorsicht! Wechselwirkungskräfte nicht mit Gleichgewichtskräften an ein und demselben Körper verwechseln! | Vorsicht! Wechselwirkungskräfte nicht mit Gleichgewichtskräften an ein und demselben Körper verwechseln! | ||
| + | |||
| + | <br clear=all> | ||
===2.2 Eindimensionale Bewegungen=== | ===2.2 Eindimensionale Bewegungen=== | ||
====Der freie Fall==== | ====Der freie Fall==== | ||
| + | [[Datei:PisaGravedad.gif|left]] | ||
| + | '''Alle Körper fallen am gleichen Ort gleich schnell''', sofern es gelingt, den Einfluss der Luft auszuschalten (--> freier Fall). | ||
| + | |||
| + | [https://www.youtube.com/watch?v=1VT4lroSNqs Freier Fall in der Vakuumröhre - Realexperiment von cg-physics] bei YouTube.com | ||
| − | |||
Die Ursache für den Fall ist die '''Gravitation''' (Massenanziehung): | Die Ursache für den Fall ist die '''Gravitation''' (Massenanziehung): | ||
| + | Gewichtskraft <math> F_{G} = m\cdot g </math> | ||
| + | Mit dem Grundgesetz der Mechanik: <math> m\cdot a = m\cdot g \Longleftrightarrow a = g </math> | ||
| − | Die Fallbeschleunigung ist nichts anderes als der Ortsfaktor. | + | Die Fallbeschleunigung ist nichts anderes als der Ortsfaktor <math> g = 9,81 \frac{m}{s^2} = 9,81 \frac{N}{kg} </math> (unabhängig von der Masse!). |
Der freie Fall ist eine Bewegung aus der Ruhe mit konstanter Beschleunigung (<math>a=g \ </math>), somit lauten die '''Bewegungsgleichungen''' | Der freie Fall ist eine Bewegung aus der Ruhe mit konstanter Beschleunigung (<math>a=g \ </math>), somit lauten die '''Bewegungsgleichungen''' | ||
| Zeile 231: | Zeile 253: | ||
wenn <math>s \ </math> die Fallstrecke und <math>t \ </math> die Fallzeit ist. | wenn <math>s \ </math> die Fallstrecke und <math>t \ </math> die Fallzeit ist. | ||
| + | ''(Siehe auch [https://www.leifiphysik.de/mechanik/freier-fall-senkrechter-wurf Freier Fall und senkrechter Wurf] bei LeiFi-Physik)'' | ||
| + | |||
| + | <br clear=all> | ||
====Harmonische Schwingungen==== | ====Harmonische Schwingungen==== | ||
| + | |||
| + | [[Datei:Federpendel.gif]] | ||
Eine '''mechanische Schwingung''' ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage. | Eine '''mechanische Schwingung''' ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage. | ||
| Zeile 256: | Zeile 283: | ||
|} | |} | ||
| − | Betrachtet man das '''Zeit-Ort-Diagramm''' einer Schwingung, so heißt diese '''harmonische Schwingung''', wenn | + | ''(Siehe auch [https://www.youtube.com/watch?v=hm_df3Oa_f8 Mechanische Schwingungen 1 - Grundbegriffe] Video von LeiFi-Physik bei Youtube.com und [https://www.leifiphysik.de/mechanik/mechanische-schwingungen Mechanische Schwingungen] bei LeiFi-Physik)'' |
| + | |||
| + | |||
| + | Betrachtet man das '''Zeit-Ort-Diagramm''' einer Schwingung, so heißt diese '''harmonische Schwingung''', wenn ihr Verlauf sinus- bzw. kosinusförmig ist: | ||
| + | |||
| + | [[Datei:Harmonischeschwingung.jpg|800px]] | ||
| + | |||
| + | Daraus kann man für die '''Auslenkung''' <math> y(t) \ </math> die Form <math> y(t) = A\cdot sin(\varphi) \ </math> erkennen. | ||
| + | ''(Zum Üben: [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zu-t-y-diagrammen-mechanischer-schwingungen Quiz zu t-y-Diagrammen bei Schwingungen] bei LeiFi-Physik)'' | ||
| − | |||
| − | Den Term <math>\frac{2\pi}{T}</math> bezeichnet man auch als '''Kreisfrequenz''' <math>\omega </math>: | + | Den Term <math>\frac{2\pi}{T}</math> bezeichnet man auch als '''Kreisfrequenz''' (bzw. Winkelgeschwindigkeit) <math>\omega </math>: |
{| border="1" cellspacing="0" cellpadding="10" | {| border="1" cellspacing="0" cellpadding="10" | ||
| Zeile 267: | Zeile 301: | ||
|} | |} | ||
| − | + | ''(Zur Kreisfrequenz siehe: [https://studyflix.de/ingenieurwissenschaften/kreisfrequenz-2560?topic_id=28 Kreisfrequenz und Frequenz] bei studyflix.de)'' | |
| + | |||
| + | Es ergibt sich die '''Schwingungsgleichung''' einer harmonischen Schwingung für die '''Auslenkung''': | ||
{| border="1" cellspacing="0" cellpadding="10" | {| border="1" cellspacing="0" cellpadding="10" | ||
|<math>y(t) = A\cdot sin(\frac{2\pi}{T}\cdot t) = A\cdot sin(\omega t) \ </math> | |<math>y(t) = A\cdot sin(\frac{2\pi}{T}\cdot t) = A\cdot sin(\omega t) \ </math> | ||
|} | |} | ||
| + | |||
| + | ''(Siehe auch [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/sinusfunktion Sinusfunktion] bei LeiFi-Physik)'' | ||
| Zeile 281: | Zeile 319: | ||
wobei <math>m \ </math> die Masse des schwingenden Körpers und <math>D \ </math> die Federkonstante (Federhärte) ist. | wobei <math>m \ </math> die Masse des schwingenden Körpers und <math>D \ </math> die Federkonstante (Federhärte) ist. | ||
| + | |||
| + | ''(Siehe auch [https://www.youtube.com/watch?v=JGY8HytPE6M Federpendel] Video von Ulrih Schütz bei Youtube.com)'' | ||
| Zeile 290: | Zeile 330: | ||
wobei <math>l \ </math> die Länge des Fadens und <math>g \ </math> die Fallbeschleunigung ist. | wobei <math>l \ </math> die Länge des Fadens und <math>g \ </math> die Fallbeschleunigung ist. | ||
| + | |||
| + | ''(Siehe auch [https://phet.colorado.edu/sims/html/pendulum-lab/latest/pendulum-lab_de.html Pendel] bei PhET und [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/schwingungsdauer-eines-fadenpendels-einflussgroessen Quiz Schwingungsdauer Fadenpendel] bei LeiFi-Physik)'' | ||
| Zeile 301: | Zeile 343: | ||
|<math>E_{ges} = E_{pot} + E_{kin} + E_{sp} = konstant \ </math> | |<math>E_{ges} = E_{pot} + E_{kin} + E_{sp} = konstant \ </math> | ||
|} | |} | ||
| + | |||
| + | |||
| + | *'''Potentielle Energie''': | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> E_{pot} = F_{G}\cdot h = m\cdot g\cdot h\ </math> | ||
| + | |} | ||
| + | |||
| + | wobei <math>\ m </math>: Masse des Körpers, <math>\ h </math>: Höhe über dem Nullniveau, | ||
| + | |||
| + | <math>\ F_{G} </math>: Gewichtskraft und <math>\ g </math>: Fallbeschleunigung oder Ortsfaktor (<math>\ g = 9,81~\frac{m}{s^{2}}</math>) | ||
| + | |||
| + | (''siehe [https://www.leifiphysik.de/mechanik/arbeit-energie-und-leistung/grundwissen/potentielle-energie Potentielle Energie] bei LeiFi-Physik'') | ||
| + | |||
| + | *'''Kinetische Energie''': | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> E_{kin} = \frac{1}{2} \cdot m \cdot v^{2} </math> | ||
| + | |} | ||
| + | |||
| + | wobei <math>\ v </math>: Geschwindigkeit des Körpers | ||
| + | |||
| + | (''siehe [https://www.leifiphysik.de/mechanik/arbeit-energie-und-leistung/grundwissen/kinetische-energie Kinetische Energie] bei LeiFi-Physik'') | ||
| + | |||
| + | *'''Spannenergie''': | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math> E_{sp} = \frac{1}{2} \cdot D \cdot s^{2}</math> | ||
| + | |} | ||
| + | |||
| + | wobei <math>\ D </math>: Federhärte der Feder und <math>\ s </math>: Ausdehnung der Feder aus der Ruhelage | ||
| + | |||
| + | (''siehe [https://www.leifiphysik.de/mechanik/arbeit-energie-und-leistung/grundwissen/spannenergie Spannenergie] bei LeiFi-Physik'') | ||
| + | |||
| + | |||
| + | '''Merke''': Für die Einheit der Energie gilt: <math> 1~J = 1~Nm = 1~\frac{kg \cdot m^{2}}{s^{2}} </math> | ||
====Impuls als Erhaltungsgröße==== | ====Impuls als Erhaltungsgröße==== | ||
| + | |||
| + | [https://youtu.be/Pnj-5570M84 Impulsübertragung mit 7 Stahlkugeln von ETH D-PHYS Vorlesungsexperimente bei YouTube.com] | ||
Der Impuls <math>p \ </math> eines Körpers ist das Produkt aus seiner Masse <math>m \ </math> und seiner Geschwindigkeit <math>v \ </math>: | Der Impuls <math>p \ </math> eines Körpers ist das Produkt aus seiner Masse <math>m \ </math> und seiner Geschwindigkeit <math>v \ </math>: | ||
| Zeile 311: | Zeile 391: | ||
|} | |} | ||
| − | Ähnlich wie für die Energie gilt auch für den Impuls ein Erhaltungssatz: | + | '''Merke''': Einheit des Impulses: <math> 1~Ns = 1~\frac{kg \cdot m}{s} </math> |
| + | |||
| + | |||
| + | Ähnlich wie für die Energie gilt auch für den '''Impuls''' ein '''Erhaltungssatz''': | ||
| + | |||
| + | In einem abgeschlossenen System ohne Reibung bleibt der Gesamtimpuls erhalten: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | |<math>p_{ges} = p_{1} + p_{2} + ... = konstant \ </math> | ||
| + | |} | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/impulserhaltung-und-stoesse Impulserhaltung und Stöße] bei LeiFi-Physik | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/impulserhaltung-und-stoesse/aufgabe/quiz-zu-stoessen Quiz zu Stößen] bei LeiFi-Physik | ||
| + | |||
| + | [https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_de.html Stoß Labor] bei PhET | ||
| + | |||
| + | [https://youtu.be/fRUv76so7wQ Zentraler, vollkommen unelastischer Stoß - einfache Fälle mit Formel und Erklärung] von WebPhysik bei YouTube.com | ||
| + | |||
| + | [https://youtu.be/VUo7jeHj_wI Zentraler elastischer Stoß - einfache Fälle mit Formel und Erklärung] von WebPhysik bei YouTube.com | ||
===2.3 Zweidimensionale Bewegungen=== | ===2.3 Zweidimensionale Bewegungen=== | ||
====Waagrechter Wurf==== | ====Waagrechter Wurf==== | ||
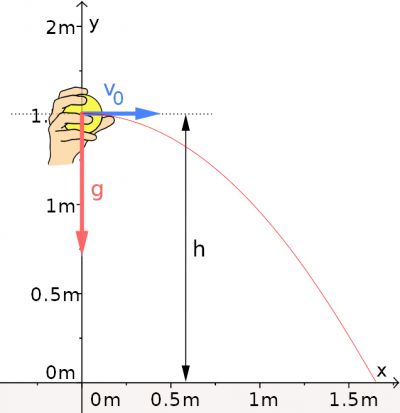
| + | [[Datei:Waagrechter Wurf.jpg|400px|right]] | ||
| + | Ein waagrechter Wurf mit der Abwurfgeschwindigkeit <math>v_0 \ </math> lässt sich zusammensetzen aus: | ||
| + | |||
| + | * einer gleichförmigen Bewegung in horizontaler <math>x</math>-Richtung, für die gilt: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>x(t) = v_0\cdot t \ </math> | ||
| + | |} | ||
| + | * und einer gleichmäßig beschleunigten Bewegung in vertikaler <math>y</math>-Richtung, für die gilt: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>y(t) = - \frac{1}{2}\cdot g\cdot t^2 \ </math> | ||
| + | |} | ||
| + | wobei <math>t \ </math> die Zeit und <math>g \ </math> die Fallbeschleunigung ist. | ||
| + | |||
| + | Die '''Bahnkurve''' des waagrechten Wurfs ist eine '''Parabel''': | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>y = - \frac{g}{2v_0^2}\cdot x^2 \ </math> | ||
| + | |} | ||
| + | |||
| + | Die '''Geschwindigkeit''' zur Zeit <math>t \ </math> lässt sich berechnen mit: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>v(t) = \sqrt{v_0^2 + (g\cdot t)^2} \ </math> | ||
| + | |} | ||
| + | |||
| + | Die '''Wurfdauer''' <math>t_w \ </math> ist: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>t_w = \sqrt{\frac{2h}{g}} \ </math> | ||
| + | |} | ||
| + | wobei <math>h \ </math> die Abwurfhöhe ist. | ||
| + | |||
| + | Die '''Wurfweite''' <math>x_{max} \ </math> ist: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>x_{max} = v_0 \cdot t_w = v_0\cdot \sqrt{\frac{2h}{g}} \ </math> | ||
| + | |} | ||
| + | |||
| + | Als '''Endgeschwindigkeit''' beim waagrechter Wurf ergibt sich: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>v = \sqrt{v_0^2 + 2gh} \ </math> | ||
| + | |} | ||
| + | |||
| + | [https://www.youtube.com/watch?v=OkXx3Ki9vwo Der waagerechte Wurf: Das musst du wissen! - Physik Duden Learnattack] bei Youtube.com | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/grundwissen/waagerechter-wurf Waagerechter Wurf] bei LeiFi-Physik | ||
| + | |||
====Gleichförmige Kreisbewegung==== | ====Gleichförmige Kreisbewegung==== | ||
| + | [[Datei:Zentripetalkraft.png|500px|right]] | ||
| − | + | [https://www.youtube.com/watch?v=-K5O2L2xhtk Kreisbewegung Teil 1 (Grundbegriffe, Umlaufdauer, Frequenz, Beispiele)] Video von LeiFi-Physik bei YouTube.com | |
| − | Für den Drehwinkel <math>\varphi \ </math> (im Bogenmaß!) gilt: | + | [https://www.youtube.com/watch?v=3rB2GBc6U00 Kreisbewegung Teil 2 (Bahn- und Winkelgeschwindigkeit, Drehwinkel, Bogenmaß)] Video von LeiFi-Physik bei YouTube.com |
| + | |||
| + | Die '''Kreisbewegung''' ist eine periodische Bewegung mit der '''Umlaufdauer''' <math>T \ </math>. Die '''Frequenz''' <math>f=\frac{1}{T} \ </math> gibt die Anzahl der Umläufe pro Zeiteinheit an. | ||
| + | |||
| + | Für den '''Drehwinkel''' <math>\varphi \ </math> (im Bogenmaß!) gilt: | ||
{| border="1" cellspacing="0" cellpadding="10" | {| border="1" cellspacing="0" cellpadding="10" | ||
| Zeile 350: | Zeile 497: | ||
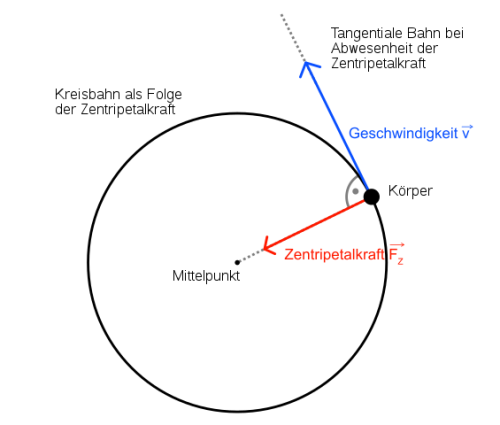
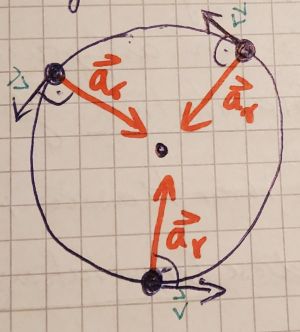
Der Betrag der Bahngeschwindigkeit <math>\overrightarrow{v}</math> bleibt bei einer gleichförmigen Kreisbewegung konstant, aber ihre Richtung ändert sich ständig: | Der Betrag der Bahngeschwindigkeit <math>\overrightarrow{v}</math> bleibt bei einer gleichförmigen Kreisbewegung konstant, aber ihre Richtung ändert sich ständig: | ||
| + | |||
| + | [[Datei:Zentripetalbeschleunigung.jpg|300px]] | ||
| + | |||
| + | Um diese Richtungsänderung zu gewährleisten, ist eine '''Zentripetalbeschleunigung''' <math>\vec a_r \ </math> nötig, die stets senkrecht zur Bewegungsrichtung zum Kreismittelpunkt zeigt. | ||
| + | |||
| + | Dafür gilt: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>a_r = v \cdot \frac{\Delta \varphi}{\Delta t} = v \cdot \omega = \omega^{2} \cdot r = \frac{v^{2}}{r} \ </math> | ||
| + | |} | ||
| + | |||
| + | Nach dem Grundgesetz der Mechanik wirkt also die zugehörige Kraft | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>F_r = m \cdot a_r = m \cdot \omega^{2} \cdot r = m \cdot \frac{v^{2}}{r} \ </math> | ||
| + | |} | ||
| + | |||
| + | Diese heißt '''Zentripetalkraft''' und ist stets zum Mittelpunkt der gleichförmigen Kreisbewegung gerichtet. | ||
| + | |||
| + | Ein mitfahrender Beobachter auf der Kreisbahn, auf den die Zentripetalkraft nicht direkt wirkt, empfindet eine vom Betrag her gleich große Trägheitskraft (Scheinkraft) radial nach außen, die sogenannte '''Zentrifugalkraft'''. | ||
| + | |||
| + | [https://www.youtube.com/watch?v=fK2gNdyQyQ8 Kreisbewegung Teil 3 (Zentripetalkraft, Zentrifugalkraft)] Video von LeiFi-Physik bei YouTube.com | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/kreisbewegung Kreisbewegung] bei LeiFi-Physik | ||
| + | |||
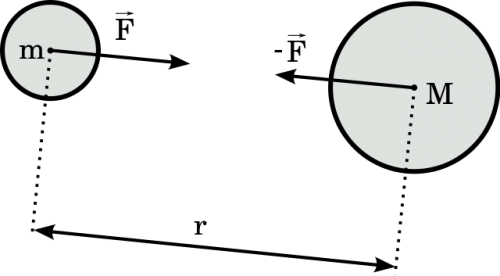
====Das Gravitationsgesetz==== | ====Das Gravitationsgesetz==== | ||
| + | [[Datei:Universal gravitation.png|500px|right]] | ||
| + | |||
| + | [https://www.youtube.com/watch?v=QOGP98uGheU GRAVITATION - Kraft, die alles zusammenhält SPACETIME Doku] von WELT bei YouTube.com | ||
| + | |||
| + | |||
| + | Alle Körper haben eine Masse. Es gibt in der Natur eine Wechselwirkung zwischen Körpern aufgrund ihrer Masse - diese wird '''Gravitation''' genannt. | ||
| + | |||
| + | Zwei Körper ziehen sich wegen ihrer Massen <math>m, M \ </math> gegenseitig an, jedoch hängt diese '''Gravitationskraft''' <math>F_{Grav} \ </math> auch von dem Abstand <math>r \ </math> der Körper ab. | ||
| + | |||
| + | Newton fand heraus: | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>F_{Grav} = G \cdot \frac{m\cdot M}{r^2} \ </math> | ||
| + | |} | ||
| + | |||
| + | mit der '''Gravitationskonstante''' <math>G = 6,67\cdot 10^{-11}~\frac{m^3}{kg\cdot s^2} \ </math> | ||
| + | |||
| + | Die '''Gewichtskraft''' eines Körpers auf der Erde ist nichts anderes als die Gravitationskraft der Erde auf diesen Körper: | ||
| + | |||
| + | <math>F_G = m\cdot g = G \cdot \frac{m\cdot M_{Erde}}{r_{Erde}^2} = F_{Grav} \ </math> | ||
| + | |||
| + | also ist <math>g = G \cdot \frac{M_{Erde}}{r_{Erde}^2} = 6,67\cdot 10^{-11}~\frac{m^3}{kg\cdot s^2}\cdot \frac{5,97\cdot 10^{24}~kg}{(6,371\cdot 10^6~m)^2} = 9,81~\frac{m}{s^2} \ </math> | ||
| + | |||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/gravitationsgesetz-und-feld Gravitationsgesetz] bei LeiFi-Physik | ||
| + | |||
===2.4 Grenzen der Newton'schen Mechanik=== | ===2.4 Grenzen der Newton'schen Mechanik=== | ||
====Kausalität==== | ====Kausalität==== | ||
| + | [https://www.leifiphysik.de/waermelehre/deterministisches-chaos Deterministisches Chaos] bei LeiFi-Physik | ||
| + | |||
| + | |||
| + | Prinzip der '''schwachen Kausalität''': ''Gleiche Ursachen haben gleiche Wirkung''. | ||
| + | |||
| + | Prinzip der '''starken Kausalität''': ''Ähnliche Ursachen führen zu ähnlichen Wirkungen''. | ||
| + | |||
| + | '''Deterministisches Chaos''' ist ein zufällig erscheinendes Verhalten eines dynamischen Systems, das jedoch deterministischen Regeln folgt. Das Verhalten wird nicht durch zufällige äußere Umstände verursacht, sondern folgt aus den Eigenschaften des Systems selbst. Es lässt sich nicht langfristig vorhersagen, ist nicht reproduzierbar. Dies tritt trotz deterministischer Dynamik auf, da die Startbedingungen eines realen physikalischen Systems nicht exakt wiederholt werden können. | ||
| + | |||
| + | Das heißt, für chaotische Systeme ''führen ähnliche Ursachen langfristig nicht zu ähnlichen Wirkungen'', die starke Kausalität ist also verletzt. | ||
| + | |||
| + | |||
| + | [https://www.youtube.com/watch?v=m5cTs7dmuPk Doppelpendel mit Gegengewichten] von Lutz Hoffmann bei YouTube.com | ||
| + | |||
| + | [https://www.youtube.com/watch?v=PIWbW2co5mY Tripendulum 300 Chaospendel von Technik und Design] von Gabriel Schneck bei YouTube.com | ||
| + | |||
| + | [https://www.youtube.com/watch?v=1IHwrpYouBA Was ist Kausalität?] von BR alpha centauri mit Harald Lesch bei YouTube.com | ||
| + | |||
====Spezielle Relativitätstheorie==== | ====Spezielle Relativitätstheorie==== | ||
| + | |||
| + | [https://www.youtube.com/watch?v=IXFf2mRxnkY Das Geheimnis der Zeit - Einsteins Relativitätstheorie] bei YouTube.com | ||
| + | |||
| + | [https://www.youtube.com/watch?v=8wb6LZtNs04 Das Relativitätsprinzip] bei Youtube.com | ||
| + | |||
| + | [https://www.youtube.com/watch?v=mt0vKjpAHfg Relativität in der SRT] bei YouTube.com | ||
| + | |||
| + | |||
| + | '''Postulate''' | ||
| + | |||
| + | '''P1 Relativitätsprinzip''' | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | Die Naturgesetze gelten in allen gleichförmig zueinander bewegten Bezugssystemen in gleicher Weise. | ||
| + | |} | ||
| + | |||
| + | '''P2 Konstanz der Lichtgeschwindigkeit''' | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | Die Vakuumlichtgeschwindigkeit <math>c = 2,99792\cdot 10^8~\frac{m}{s} \ </math> ist unabhängig von der Bewegung der Lichtquelle und vom Bezugssystem, in dem sie gemessen wird, immer gleich groß. | ||
| + | |} | ||
| + | |||
| + | |||
| + | '''Folgerungen''' | ||
| + | |||
| + | '''F1 Zeitdehnung''' | ||
| + | |||
| + | Bewegte Uhren gehen für einen äußeren Beobachter langsamer: <math>t = \frac{t'}{\sqrt{1-\frac{v^2}{c^2}}} \ </math> | ||
| + | |||
| + | '''F2 Längenkontraktion''' | ||
| + | |||
| + | Körper erscheinen für einen äußeren Beobachter in Bewegungsrichtung verkürzt: <math>l = l' \cdot \sqrt{1-\frac{v^2}{c^2}} \ </math> | ||
| + | |||
| + | '''F3 Relativität der Gleichzeitigkeit''' | ||
| + | |||
| + | Der Begriff "gleichzeitig" ist nicht absolut, sondern relativ, also abhängig vom Bezugssystem des Beobachters. | ||
| + | |||
| + | '''F4 Raumzeit''' | ||
| + | |||
| + | Raum und Zeit stehen in direktem Zusammenhang und sind vom Bewegungszustand des Bezugssystems abhängig (vierdimensionale Raumzeit). | ||
| + | |||
| + | Um Raum zu überwinden, braucht man Zeit, aber die Lichtgeschwindigkeit ist das absolute Tempolimit! Raum lässt sich also nicht sofort überwinden, jeder Blick ist ein Blick in die Vergangenheit. | ||
| + | |||
| + | '''F5 Massenzunahme''' | ||
| + | |||
| + | Die Masse eines Körpers nimmt mit seiner Geschwindigkeit für einen äußeren Beobachter zu: <math>m = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \ </math> | ||
| + | |||
| + | '''F6 Relativistische Energie / Äquivalenz von Masse und Energie''' | ||
| + | |||
| + | Die Gesamtenergie eines Körpers und seine dynamische Masse sind zueinander direkt proportional, Masse und Energie sind äquivalent: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>E = m \cdot c^2 \ </math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | [https://www.leifiphysik.de/relativitaetstheorie Relativitätstheorie] bei LeiFi-Physik | ||
| + | |||
==3. Wellenlehre und Quantenphysik== | ==3. Wellenlehre und Quantenphysik== | ||
====3.1 Wellenphänomene==== | ====3.1 Wellenphänomene==== | ||
| + | |||
| + | [https://phet.colorado.edu/sims/html/waves-intro/latest/waves-intro_de.html Wellen Einführung] Simulation bei PhET | ||
| + | |||
| + | [https://www.youtube.com/watch?v=c6fVKRF2T9c Arten von Wellen] Video von LeiFi-Physik bei Youtube.com | ||
| + | |||
| + | [https://www.leifiphysik.de/mechanik/mechanische-wellen Mechanische Wellen] bei LeiFi-Physik | ||
| + | |||
Eine '''Welle''' ist die Ausbreitung einer Auslenkung (Schwingung) in einem Medium (z.B. Wasser, Luft oder auch Vakuum (el. magn. Wellen!)). | Eine '''Welle''' ist die Ausbreitung einer Auslenkung (Schwingung) in einem Medium (z.B. Wasser, Luft oder auch Vakuum (el. magn. Wellen!)). | ||
| Zeile 370: | Zeile 648: | ||
| − | Die Geschwindigkeit, mit der sich eine Auslenkung im Medium ausbreitet, heißt Ausbreitungsgeschwindigkeit v der Welle. | + | [https://www.youtube.com/watch?v=Mh-_H2_42NM Beschreibung von Wellen] Video von LeiFi-Physik bei Youtube.com |
| + | |||
| + | [https://phet.colorado.edu/sims/html/wave-on-a-string/latest/wave-on-a-string_de.html Seilwelle] Simulation bei PhET | ||
| + | |||
| + | |||
| + | Die Geschwindigkeit, mit der sich eine Auslenkung im Medium ausbreitet, heißt '''Ausbreitungsgeschwindigkeit''' v der Welle: | ||
| + | {| border="1" cellspacing="0" cellpadding="10" | ||
| + | | <math>v = \lambda \cdot f \ </math> | ||
| + | |} | ||
| + | wobei <math> \lambda \ </math> die Wellenlänge und <math> f \ </math> die Frequenz ist. | ||
| − | Eigenschaften von Wellen: | + | '''Eigenschaften von Wellen:''' |
Wellen können reflektiert, gebrochen, gebeugt werden oder sich überlagern: | Wellen können reflektiert, gebrochen, gebeugt werden oder sich überlagern: | ||
| + | |||
| + | *'''Reflexion:''' | ||
| + | Wellen werden an Hindernissen zurückgeworfen. | ||
| + | |||
| + | *'''Brechung:''' | ||
| + | Beim Übergang in ein anderes Medium verändern Wellen ihre Ausbreitungsrichtung. | ||
| + | |||
| + | *'''Beugung:''' | ||
| + | Wellen breiten sich hinter Hindernissen auch in den Schattenraum aus. | ||
| + | |||
| + | *'''Interferenz:''' | ||
| + | Wellen überlagern sich. Dabei kommt es in bestimmten Bereichen zur Verstärkung und in anderen zur Auslöschung. | ||
| + | |||
| + | [https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_de.html Lichtbrechung] Simulation bei PhET | ||
| + | |||
| + | [https://www.youtube.com/watch?v=cnVkYK2L-wI Beugung von Wellen] Video von LeiFi-Physik bei Youtube.com | ||
| + | |||
| + | [https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_de.html Wellen Interferenz] Simulation bei PhET | ||
| + | |||
| + | [https://www.youtube.com/watch?v=koZ2c_Olieg Interferenz] Video von LeiFi-Physik bei Youtube.com | ||
| + | |||
====3.2 Wellen- und Teilchencharakter des Lichts==== | ====3.2 Wellen- und Teilchencharakter des Lichts==== | ||
| + | |||
====3.3 Quantenobjekte==== | ====3.3 Quantenobjekte==== | ||
Aktuelle Version vom 3. Juli 2022, 19:20 Uhr
Physik GWPh7 GWPh8 GWPh9 GWPh10 SchulheftPh8 SchulheftPh9 SchulheftPh11 SchulheftPh12
Inhaltsverzeichnis
- 1 0. Wiederholung
- 2 1. Astronomie
- 2.1 1.1 Sternkunde im alten Ägypten und Babylonien
- 2.2 1.2 Das Weltbild der alten Griechen
- 2.3 1.3 Kopernikus und Galilei - heliozentrisches Weltbild
- 2.4 1.4 Die keplerschen Gesetze zur Planetenbewegung
- 2.5 1.5 Unser Sonnensystem
- 2.6 1.6 Unsere Milchstraße und andere Galaxien
- 2.7 1.7 Der Urknall
- 2.8 1.8 Schwarze Löcher
- 3 2. Die Mechanik Newtons
- 4 3. Wellenlehre und Quantenphysik
0. Wiederholung
(siehe Grundwissen Physik 9 oder LeiFi-Physik)
1. Astronomie
(siehe Astronomie bei LeiFi-Physik)
1.1 Sternkunde im alten Ägypten und Babylonien
In den alten Hochkulturen der Menschheit zählte die Festlegung eines Zeitmaßes als wichtigstes Motiv für die Beobachtung des Himmels (= Astronomie). So wurden bereits Kalender geschaffen und der Himmel als natürliche Uhr genutzt.
Der Zusammenhang des Überirdischen mit den Gestirnen wurde durch die Festlegung als Götter in den diversen Religionen sichtbar. Dieser Glaube, der bis heute in der Astrologie seine Fortsetzung hat, führte auch zum Wunsch bestimmte Himmels-Konstellationen, z.B. die Mond- und Sonnenfinsternisse zeitlich genau vorhersagen zu können. Hierzu waren exakte Beobachtungen und genaue Aufzeichnungen vonnöten.
(siehe Astronomie - Einführung Geschichte bei LeiFi-Physik)
(Tipp: Mit der kostenlosen, quelloffenen Planetarium-Software Stellarium bekommt man einen guten Eindruck vom Sternenhimmel, so wie man ihn mit bloßem Auge, Fernglas oder Teleskop sehen kann)
1.2 Das Weltbild der alten Griechen
Die Griechen fassten ihre zahlreichen Beobachtungsergebnisse der Gestirne im geozentrischen Weltbild zusammen. Bei ihm bewegen sich alle Himmelskörper auf kreisförmigen Bahnen um die Erde.
Bedeutsamen Einfluss auf das griechische Weltbild hatten Platon, Hipparch, Ptolemäus und Aristoteles.
Aristarch entwickelte ein heliozentrisches Weltmodell. Er rückte die Sonne in den Mittelpunkt des Weltalls. Seine richtigen Argumente (Erdrotation in 24 Stunden, Kreisbahn der Erde um die Sonne im Laufe eines Jahres) konnten sich nicht durchsetzen und erst Kopernikus hat sie sich wieder zu eigen gemacht.
Das geozentrische Weltbild des Aristoteles und dessen Perfektionierung durch Ptolemäus dominierte bis ins 16. Jahrhundert.
(siehe Astronomie im Altertum bei LeiFi-Physik)
1.3 Kopernikus und Galilei - heliozentrisches Weltbild
Kopernikus vertrat in seinem Buch DE REVOLUTIONIBUS ORBIUM COELESTIUM ein heliozentrisches Weltbild. Das Buch erschien erst mit seinem Tod.
Seine wichtigsten Thesen darin waren:
- Die Himmelskörper bewegen sich um die Sonne.
- Die Bewegung der Sonne und der Fixsternsphäre ist eine Folge der Erdrotation.
- Die Erde läuft auf der Ekliptik in einem Jahr einmal um die Sonne .
- Der Mond umkreist dabei die Erde.
- Die Rotationsachse der Erde ist gegenüber der Ekliptikebene um 23,5° geneigt, womit sich die Jahreszeiten erklären lassen.
Galileo Galilei baute das in Holland erfundene Fernrohr nach und machte damit astronomische Beobachtungen:
- Er entdeckte die Gebirgslandschaft des Mondes. Der Mond war also ein Körper, der mit der Erde zu vergleichen ist.
- Er sah und beschrieb den Sternenreichtum der Milchstraße, die Phasen der Venus und vier Jupitermonde.
- Galilei entdeckte die Sonnenflecken.
Aufgrund seiner Beobachtungen unterstütze er das heliozentrische Weltbild des Kopernikus und kam deswegen in Konflikt mit der damals üblichen Auslegeung der christlichen Lehre.
(siehe Astronomie im Mittelalter bei LeiFi-Physik)
1.4 Die keplerschen Gesetze zur Planetenbewegung
Johannes Kepler erbte von Tycho Brahe eine Fülle von sehr genauen Datenreihen über die Position der Planeten. Die Schwierigkeit war, darin einen Zusammenhang zu erkennen, da die Umlaufbewegung der anderen Planeten von der Erde betrachtet wird, die selbst die Sonne umkreist. Im Gegensatz zu Brahe glaubte Kepler an das heliozentrische System. Ausgehend von diesem Gerüst verbrachte er zwanzig Jahre mit sorgfältigen Versuchen und Überprüfungen, um den Daten einen Sinn zu geben.
Seine drei Planetengesetze:
1. Die Planeten bewegen sich auf elliptischen Bahnen, in deren einen Brennpunkt die Sonne ist.
2. Die Verbindungslinie zwischen Sonne und Planet überstreicht in gleichen Zeiten gleich große Flächen.
3. Für die Umlaufzeiten zweier Planeten und der großen Halbachsen ihrer Bahnen gilt:
(siehe Kepler-Gesetze bei LeiFi-Physik)
1.5 Unser Sonnensystem
(siehe Sonnensystem bei Wikipedia und nineplanets.org und Planetary Science bei NASA und Welcome to the planets bei NASA und Eyes on the Solar System bei NASA oder Solarsystem Scope von SUNAEON)
(Daten der Himmelskörper im Sonnensystem siehe Astronomische Daten bei LeiFi-Physik)
(Tipp: Mit der Echtzeit-Weltraumsimulation Celestia kann man unser Universum in drei Dimensionen visuell erforschen)
1.6 Unsere Milchstraße und andere Galaxien
Die Galaxie (Sternsystem) in der wir leben nennen wir Milchstraße. Sie ist eine Spiralgalaxie mit etwa 100000 Lichtjahren Durchmesser und besteht aus über 100 Milliarden Sternen. In ihrem Zentralgebiet (etwa 28000 Lichtjahre von uns entfernt) sitzt wahrscheinlich ein extrem kompaktes und massereiches schwarzes Loch. Um die relativ flache Scheibenebene (Dicke bis zu 16000 Lichtjahre) befinden sich viele ältere Kugelsternhaufen, die den galaktischen Halo bilden. Weiterhin ist die Milchstraße in eine Korona genannte Hülle aus dunkler Materie eingebettet.
Die Milchstraße, die Andromeda-Galaxie, der Dreiecksnebel und die Magellansche Wolken werden der sogenannten lokalen Gruppe zugeordnet, einer vergleichsweisen kleinen Zusammenballung von Galaxien.
In unserem Universum gibt es eine Vielzahl von Galaxien und Galaxienhaufen. Das kosmologische Prinzip sagt aus, dass kein Punkt im Universum in einer besonderen Weise ausgezeichnet ist.
Astronomische Längeneinheiten
1 AE ("Astronomische Einheit") = 149,6 Millionen km ist die mittlere Entfernung zwischen Erde und Sonne.
1 ly ("Lichtjahr") = 63284 AE = 9,467 Billionen km ist die Entfernung, die das Licht im Vakuum in einem Erdjahr zurücklegt.
1 pc ("Parsec") = 3,26 ly = 206306 AE = 30,86 Billionen km ist die Entfernung unter der man 1 AE unter dem Winkel 1 Bogensekunde sieht.
1.7 Der Urknall
Der Urknall (Big Bang) ist nach dem Standardmodell der Kosmologie der Beginn des Universums. Im Rahmen der Urknalltheorie wird auch das frühe Universum beschrieben. Der Urknall bezeichnet keine Explosion in einem bestehenden Raum, sondern die gemeinsame Entstehung von Materie, Raum und Zeit aus einer ursprünglichen Singularität. Man geht davon aus, dass unser Universum vor etwa 14 Milliarden Jahren durch den Urknall entstanden ist und sich seitdem immer weiter ausdehnt und abkühlt.
Das hubblesche Gesetz sagt aus, dass sich zwei Galaxien umso schneller voneinander entfernen, je größer ihr Abstand zueinander ist.
Die Fluchtbewegung der Galaxien, die 3K-Hintergrundstrahlung und die Elementhäufigkeit im Universum sind die wichtigsten Hinweise für die Theorie des Urknalls.
1.8 Schwarze Löcher
Ein Schwarzes Loch ist ein massives Objekt im Universum, das durch sein Gravitationsfeld das Raumzeitgefüge um sich herum so verzerrt, dass weder Materie noch Licht aus dieser Region nach außen gelangen können.
Ein Schwarzes Loch entsteht, wenn Materie eine bestimmte Dichte überschreitet. Die Allgemeine Relativitätstheorie besagt, dass massive Objekte durch ihr Gravitationsfeld den Raum um sich herum krümmen. Dies macht sich dadurch bemerkbar, dass Lichtstrahlen in der Nähe eines solchen Objekts nicht mehr geradlinig verlaufen. Sie werden wie von einer Sammellinse in Richtung des Objekts abgelenkt. Dieser Effekt macht sich bereits bei unserer Sonne bemerkbar, ist aber bei Neutronensternen oder noch dichteren Objekten entsprechend stärker. Ist das massive Objekt sehr klein, kann es das Licht auf eine Kreisbahn zwingen und den Raum komplett 'abschnüren'. Ein Schwarzes Loch ist entstanden. In seinem Zentrum befindet sich eine Singularität, ein Punkt unendlicher Dichte und Gravitation.
Die Größe, unterhalb der ein Objekt zu einem Schwarzen Loch wird, nennt man den Schwarzschild-Radius. Er hängt von der Masse des Objekts ab.
Der Schwarzschild-Radius ist zugleich der Ereignishorizont des Schwarzen Loches, die Grenze, innerhalb derer keine Materie oder Strahlung das Schwarze Loch mehr verlassen kann.
Je nach Größe und Entstehungsgeschichte unterscheidet man mehrere Arten von Schwarzen Löchern:
- Stellare Schwarze Löcher sind der Endzustand der Entwicklung schwerer Sterne ab der etwa zehnfachen Sonnenmasse. Sie explodieren am Ende ihres Lebens als Supernova und stoßen dabei einen Teil ihrer Materie als Gaswolke ab. Der Rest stürzt unter dem Einfluss der Schwerkraft in sich zusammen, bis sich all seine Atomkerne berühren.
- Mittelschwere Schwarze Löcher können einige hundert Sonnenmassen haben und entstehen durch Kollisionen mehrerer Sterne, z.B. in Doppel- oder Mehrfachsternsystemen.
- Supermassive Schwarze Löcher bis zur milliardenfachen Masse unserer Sonne sitzen in den Zentren der meisten Galaxien wie Spinnen in ihren Netzen. Sie haben ihre Größe durch das Ansammeln von interstellarem Gas und Staub erreicht. Das Schwarze Loch in unserer Milchstraße schätzt man auf 3,6 Millionen Sonnenmassen. In der Frühzeit des Universums waren diese supermassiven Schwarzen Löcher durch die Erhitzung der hineinstürzenden Materie die hellsten Objekte weit und breit. Man sieht sie heute noch in weiter Entfernung und ferner Vergangenheit als Quasare leuchten.
- Primordiale Schwarze Löcher haben sich bereits kurz nach dem Urknall in Raumbereichen hoher Massen- und Energiedichte gebildet. Da zu diesem Zeitpunkt extrem hoher Druck im Universum herrschte und die Materie entsprechend komprimiert war, können primordiale Schwarze Löcher theoretisch relativ wenig Masse enthalten, etwa nur wenige tausend Kilogramm.
(Text aus http://kosmologie.füreilige.de/ von Johann Christian Lotter)
2. Die Mechanik Newtons
2.1 Newtons Gesetze
Was ist eine Kraft?
Eine Kraft bewirkt eine Bewegungsänderung (--> Beschleunigung) oder eine Formveränderung.
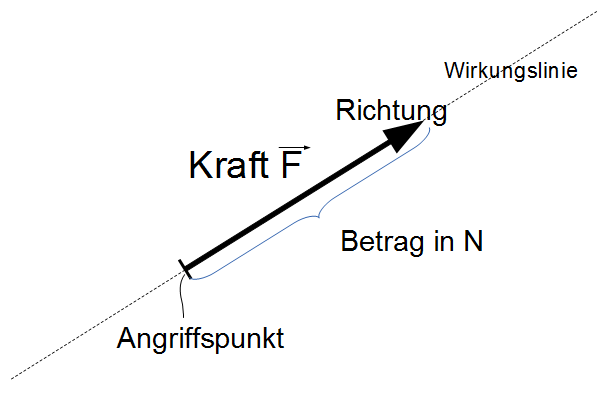
Die Wirkung einer Kraft ist von ihrem Angriffspunkt, ihrem Betrag und ihrer Richtung abhängig:
Kräfte werden in der Einheit 1 N (Newton) angegeben. Es gilt:
Die Summe aller Kräfte auf einen Körper bestimmt, ob und wie er sich bewegt.
Schiefe Ebene Simulation bei LeiFi-Physik
Zusammensetzung von Kräften
(siehe Kräfteaddition bei Leifiphysik)
Ist die Summe aller Kräfte (=Gesamtkraft) auf einen Körper gleich null, so befindet er sich im Kräftegleichgewicht.
Zerlegung von Kräften
(siehe Kräftezerlegung bei Leifiphysik)
Kräfte am Keil einfach erklärt von Educational-Animation.com bei YouTube.com
Trägheitssatz von Newton (Newton I)
| Befindet sich ein Körper im Kräftegleichgewicht, so bleibt er in Ruhe oder bewegt sich gleichförmig geradlinig weiter. |
(siehe Trägheitsgesetz von Newton bei Leifiphysik)
Video Tischdecke wegziehen - ohne Scherben von Planet Schule bei YouTube.com
Grundgesetz der Mechanik (Newton II)
Auf einen Körper der Masse m, der die Beschleunigung a erfährt, wirkt die Kraft F.
(siehe 2. Newtonsches Gesetz bei LeiFi-Physik)
Bewegungsgesetze
Für eine gleichmäßig beschleunigte Bewegung (a=konstant) eines Körpers aus der Ruhe gelten:
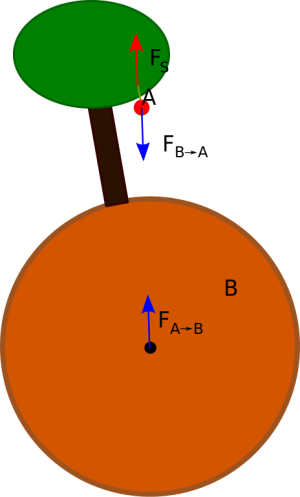
Wechselwirkungsgesetz (Newton III)
Siehe auch Kraft und Bewegungsänderung bei LeiFi-Physik
Eine Kraft, die auf einen Körper wirkt, geht immer von anderen Körpern aus.
| Übt ein Körper A eine Kraft auf den Körper B aus, so übt B auf A die Gegenkraft aus.
Kurz: "actio gegengleich reactio" |
Dabei gehören Kraft und Gegenkraft immer zusammen, sie treten paarweise auf, greifen jedoch an verschiedenen Körpern an (Wechselwirkungskräfte).
Vorsicht! Wechselwirkungskräfte nicht mit Gleichgewichtskräften an ein und demselben Körper verwechseln!
2.2 Eindimensionale Bewegungen
Der freie Fall
Alle Körper fallen am gleichen Ort gleich schnell, sofern es gelingt, den Einfluss der Luft auszuschalten (--> freier Fall).
Freier Fall in der Vakuumröhre - Realexperiment von cg-physics bei YouTube.com
Die Ursache für den Fall ist die Gravitation (Massenanziehung):
Gewichtskraft
Mit dem Grundgesetz der Mechanik:
Die Fallbeschleunigung ist nichts anderes als der Ortsfaktor (unabhängig von der Masse!).
Der freie Fall ist eine Bewegung aus der Ruhe mit konstanter Beschleunigung (), somit lauten die Bewegungsgleichungen
wenn die Fallstrecke und die Fallzeit ist.
(Siehe auch Freier Fall und senkrechter Wurf bei LeiFi-Physik)
Harmonische Schwingungen
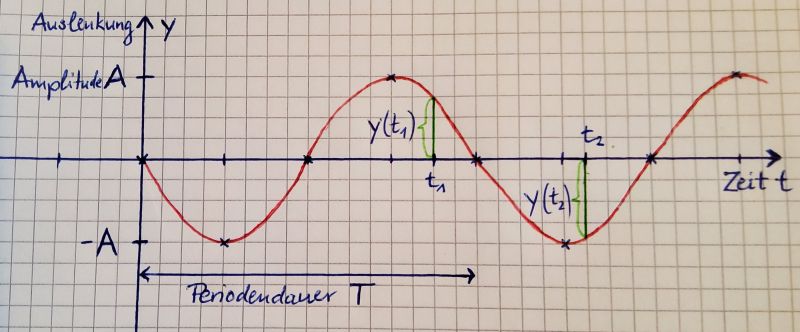
Eine mechanische Schwingung ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage.
Eine Periode ist dabei ein vollständiger Durchlauf der Bewegung, der sich anschließend wiederholt.
Die Zeit für eine Periode wird auch Schwingungsdauer oder Periodendauer genannt.
Die maximale Auslenkung aus der Gleichgewichtslage bei einer Schwingung heißt Amplitude (Schwingungsweite).
Die Frequenz einer Schwingung gibt an, wie viele (Anzahl ) Schwingungen (Perioden) pro Zeit ablaufen:
Die Einheit der Frequenz ist: ("Hertz")
Insbesondere gilt für :
(Siehe auch Mechanische Schwingungen 1 - Grundbegriffe Video von LeiFi-Physik bei Youtube.com und Mechanische Schwingungen bei LeiFi-Physik)
Betrachtet man das Zeit-Ort-Diagramm einer Schwingung, so heißt diese harmonische Schwingung, wenn ihr Verlauf sinus- bzw. kosinusförmig ist:
Daraus kann man für die Auslenkung die Form erkennen.
(Zum Üben: Quiz zu t-y-Diagrammen bei Schwingungen bei LeiFi-Physik)
Den Term bezeichnet man auch als Kreisfrequenz (bzw. Winkelgeschwindigkeit) :
(Zur Kreisfrequenz siehe: Kreisfrequenz und Frequenz bei studyflix.de)
Es ergibt sich die Schwingungsgleichung einer harmonischen Schwingung für die Auslenkung:
(Siehe auch Sinusfunktion bei LeiFi-Physik)
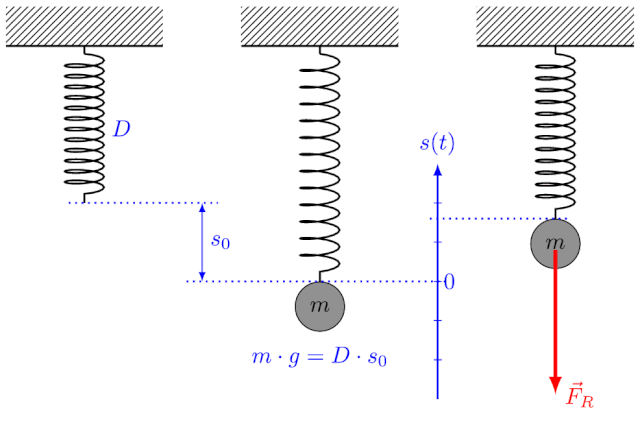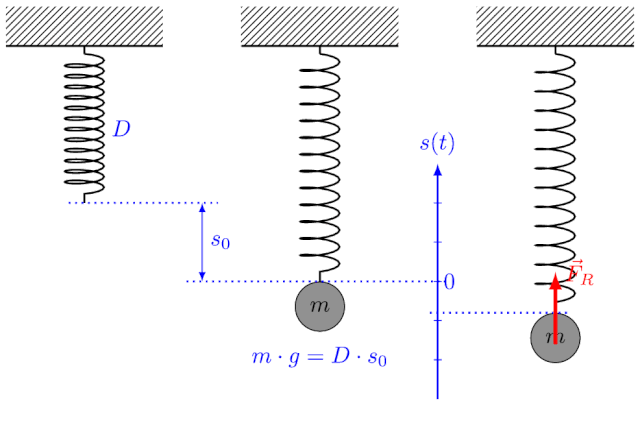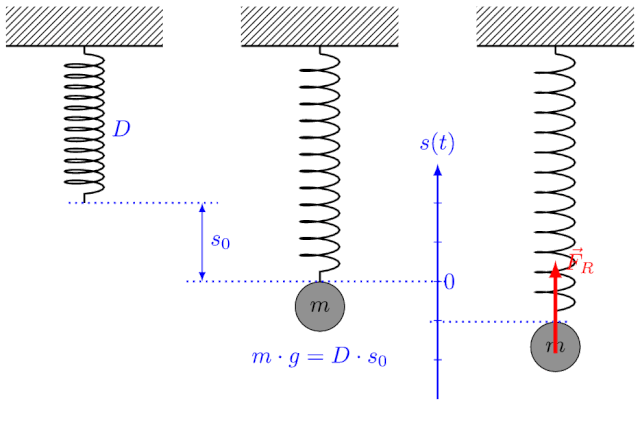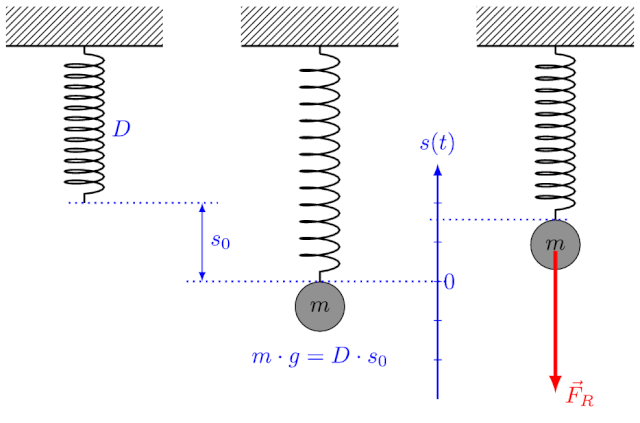
Beim Federpendel gilt für die Schwingungsdauer:
wobei die Masse des schwingenden Körpers und die Federkonstante (Federhärte) ist.
(Siehe auch Federpendel Video von Ulrih Schütz bei Youtube.com)
Beim Fadenpendel gilt bei kleinen Auslenkungen für die Schwingungsdauer:
wobei die Länge des Fadens und die Fallbeschleunigung ist.
(Siehe auch Pendel bei PhET und Quiz Schwingungsdauer Fadenpendel bei LeiFi-Physik)
Energie als Erhaltungsgröße
Energieerhaltungssatz der Mechanik:
In einem abgeschlossenen System ohne Reibung gilt:
- Potentielle Energie:
wobei : Masse des Körpers, : Höhe über dem Nullniveau,
: Gewichtskraft und : Fallbeschleunigung oder Ortsfaktor ()
(siehe Potentielle Energie bei LeiFi-Physik)
- Kinetische Energie:
wobei : Geschwindigkeit des Körpers
(siehe Kinetische Energie bei LeiFi-Physik)
- Spannenergie:
wobei : Federhärte der Feder und : Ausdehnung der Feder aus der Ruhelage
(siehe Spannenergie bei LeiFi-Physik)
Merke: Für die Einheit der Energie gilt:
Impuls als Erhaltungsgröße
Impulsübertragung mit 7 Stahlkugeln von ETH D-PHYS Vorlesungsexperimente bei YouTube.com
Der Impuls eines Körpers ist das Produkt aus seiner Masse und seiner Geschwindigkeit :
Merke: Einheit des Impulses:
Ähnlich wie für die Energie gilt auch für den Impuls ein Erhaltungssatz:
In einem abgeschlossenen System ohne Reibung bleibt der Gesamtimpuls erhalten:
Impulserhaltung und Stöße bei LeiFi-Physik
Quiz zu Stößen bei LeiFi-Physik
Stoß Labor bei PhET
Zentraler, vollkommen unelastischer Stoß - einfache Fälle mit Formel und Erklärung von WebPhysik bei YouTube.com
Zentraler elastischer Stoß - einfache Fälle mit Formel und Erklärung von WebPhysik bei YouTube.com
2.3 Zweidimensionale Bewegungen
Waagrechter Wurf
Ein waagrechter Wurf mit der Abwurfgeschwindigkeit lässt sich zusammensetzen aus:
- einer gleichförmigen Bewegung in horizontaler -Richtung, für die gilt:
- und einer gleichmäßig beschleunigten Bewegung in vertikaler -Richtung, für die gilt:
wobei die Zeit und die Fallbeschleunigung ist.
Die Bahnkurve des waagrechten Wurfs ist eine Parabel:
Die Geschwindigkeit zur Zeit lässt sich berechnen mit:
Die Wurfdauer ist:
wobei die Abwurfhöhe ist.
Die Wurfweite ist:
Als Endgeschwindigkeit beim waagrechter Wurf ergibt sich:
Der waagerechte Wurf: Das musst du wissen! - Physik Duden Learnattack bei Youtube.com
Waagerechter Wurf bei LeiFi-Physik
Gleichförmige Kreisbewegung
Kreisbewegung Teil 1 (Grundbegriffe, Umlaufdauer, Frequenz, Beispiele) Video von LeiFi-Physik bei YouTube.com
Kreisbewegung Teil 2 (Bahn- und Winkelgeschwindigkeit, Drehwinkel, Bogenmaß) Video von LeiFi-Physik bei YouTube.com
Die Kreisbewegung ist eine periodische Bewegung mit der Umlaufdauer . Die Frequenz gibt die Anzahl der Umläufe pro Zeiteinheit an.
Für den Drehwinkel (im Bogenmaß!) gilt:
()
Bei einer gleichförmigen Kreisbewegung gibt es eine konstante Winkelgeschwindigkeit :
Für eine volle Umdrehung ergibt sich
(deswegen wird auch Kreisfrequenz genannt)
Damit gilt für die Bahngeschwindigkeit :
Der Betrag der Bahngeschwindigkeit bleibt bei einer gleichförmigen Kreisbewegung konstant, aber ihre Richtung ändert sich ständig:
Um diese Richtungsänderung zu gewährleisten, ist eine Zentripetalbeschleunigung nötig, die stets senkrecht zur Bewegungsrichtung zum Kreismittelpunkt zeigt.
Dafür gilt:
Nach dem Grundgesetz der Mechanik wirkt also die zugehörige Kraft
Diese heißt Zentripetalkraft und ist stets zum Mittelpunkt der gleichförmigen Kreisbewegung gerichtet.
Ein mitfahrender Beobachter auf der Kreisbahn, auf den die Zentripetalkraft nicht direkt wirkt, empfindet eine vom Betrag her gleich große Trägheitskraft (Scheinkraft) radial nach außen, die sogenannte Zentrifugalkraft.
Kreisbewegung Teil 3 (Zentripetalkraft, Zentrifugalkraft) Video von LeiFi-Physik bei YouTube.com
Kreisbewegung bei LeiFi-Physik
Das Gravitationsgesetz
GRAVITATION - Kraft, die alles zusammenhält SPACETIME Doku von WELT bei YouTube.com
Alle Körper haben eine Masse. Es gibt in der Natur eine Wechselwirkung zwischen Körpern aufgrund ihrer Masse - diese wird Gravitation genannt.
Zwei Körper ziehen sich wegen ihrer Massen gegenseitig an, jedoch hängt diese Gravitationskraft auch von dem Abstand der Körper ab.
Newton fand heraus:
mit der Gravitationskonstante
Die Gewichtskraft eines Körpers auf der Erde ist nichts anderes als die Gravitationskraft der Erde auf diesen Körper:
also ist
Gravitationsgesetz bei LeiFi-Physik
2.4 Grenzen der Newton'schen Mechanik
Kausalität
Deterministisches Chaos bei LeiFi-Physik
Prinzip der schwachen Kausalität: Gleiche Ursachen haben gleiche Wirkung.
Prinzip der starken Kausalität: Ähnliche Ursachen führen zu ähnlichen Wirkungen.
Deterministisches Chaos ist ein zufällig erscheinendes Verhalten eines dynamischen Systems, das jedoch deterministischen Regeln folgt. Das Verhalten wird nicht durch zufällige äußere Umstände verursacht, sondern folgt aus den Eigenschaften des Systems selbst. Es lässt sich nicht langfristig vorhersagen, ist nicht reproduzierbar. Dies tritt trotz deterministischer Dynamik auf, da die Startbedingungen eines realen physikalischen Systems nicht exakt wiederholt werden können.
Das heißt, für chaotische Systeme führen ähnliche Ursachen langfristig nicht zu ähnlichen Wirkungen, die starke Kausalität ist also verletzt.
Doppelpendel mit Gegengewichten von Lutz Hoffmann bei YouTube.com
Tripendulum 300 Chaospendel von Technik und Design von Gabriel Schneck bei YouTube.com
Was ist Kausalität? von BR alpha centauri mit Harald Lesch bei YouTube.com
Spezielle Relativitätstheorie
Das Geheimnis der Zeit - Einsteins Relativitätstheorie bei YouTube.com
Das Relativitätsprinzip bei Youtube.com
Relativität in der SRT bei YouTube.com
Postulate
P1 Relativitätsprinzip
| Die Naturgesetze gelten in allen gleichförmig zueinander bewegten Bezugssystemen in gleicher Weise. |
P2 Konstanz der Lichtgeschwindigkeit
| Die Vakuumlichtgeschwindigkeit ist unabhängig von der Bewegung der Lichtquelle und vom Bezugssystem, in dem sie gemessen wird, immer gleich groß. |
Folgerungen
F1 Zeitdehnung
Bewegte Uhren gehen für einen äußeren Beobachter langsamer:
F2 Längenkontraktion
Körper erscheinen für einen äußeren Beobachter in Bewegungsrichtung verkürzt:
F3 Relativität der Gleichzeitigkeit
Der Begriff "gleichzeitig" ist nicht absolut, sondern relativ, also abhängig vom Bezugssystem des Beobachters.
F4 Raumzeit
Raum und Zeit stehen in direktem Zusammenhang und sind vom Bewegungszustand des Bezugssystems abhängig (vierdimensionale Raumzeit).
Um Raum zu überwinden, braucht man Zeit, aber die Lichtgeschwindigkeit ist das absolute Tempolimit! Raum lässt sich also nicht sofort überwinden, jeder Blick ist ein Blick in die Vergangenheit.
F5 Massenzunahme
Die Masse eines Körpers nimmt mit seiner Geschwindigkeit für einen äußeren Beobachter zu:
F6 Relativistische Energie / Äquivalenz von Masse und Energie
Die Gesamtenergie eines Körpers und seine dynamische Masse sind zueinander direkt proportional, Masse und Energie sind äquivalent:
Relativitätstheorie bei LeiFi-Physik
3. Wellenlehre und Quantenphysik
3.1 Wellenphänomene
Wellen Einführung Simulation bei PhET
Arten von Wellen Video von LeiFi-Physik bei Youtube.com
Mechanische Wellen bei LeiFi-Physik
Eine Welle ist die Ausbreitung einer Auslenkung (Schwingung) in einem Medium (z.B. Wasser, Luft oder auch Vakuum (el. magn. Wellen!)).
Mit Wellen wird nur Energie (nicht der Stoff selbst) übertragen.
Prinzipiell unterscheidet man zwischen Transversalwellen (Querwellen) und Longitudinalwellen (Längswellen).
Beschreibung von Wellen Video von LeiFi-Physik bei Youtube.com
Seilwelle Simulation bei PhET
Die Geschwindigkeit, mit der sich eine Auslenkung im Medium ausbreitet, heißt Ausbreitungsgeschwindigkeit v der Welle:
wobei die Wellenlänge und die Frequenz ist.
Eigenschaften von Wellen:
Wellen können reflektiert, gebrochen, gebeugt werden oder sich überlagern:
- Reflexion:
Wellen werden an Hindernissen zurückgeworfen.
- Brechung:
Beim Übergang in ein anderes Medium verändern Wellen ihre Ausbreitungsrichtung.
- Beugung:
Wellen breiten sich hinter Hindernissen auch in den Schattenraum aus.
- Interferenz:
Wellen überlagern sich. Dabei kommt es in bestimmten Bereichen zur Verstärkung und in anderen zur Auslöschung.
Lichtbrechung Simulation bei PhET
Beugung von Wellen Video von LeiFi-Physik bei Youtube.com
Wellen Interferenz Simulation bei PhET
Interferenz Video von LeiFi-Physik bei Youtube.com
3.2 Wellen- und Teilchencharakter des Lichts
3.3 Quantenobjekte
Physik GWPh7 GWPh8 GWPh9 GWPh10 SchulheftPh8 SchulheftPh9 SchulheftPh11 SchulheftPh12